상부 및 하부 삼각 행렬

이 페이지에서는 삼각 행렬이 무엇인지, 그리고 다양한 유형의 삼각 행렬을 예제와 함께 볼 수 있습니다. 또한 삼각 행렬의 행렬식을 계산하는 방법과 이 매우 흥미로운 행렬의 속성이 무엇인지 알아볼 것입니다. 마지막으로 삼각행렬과 관련된 행렬인 헤센베르크 행렬(Hessenberg 행렬)이 무엇인지도 설명합니다.

삼각행렬이란 무엇입니까?

삼각행렬의 정의:

삼각행렬은 주대각선 위 또는 아래의 모든 요소가 0인 정방행렬입니다.

삼각 행렬은 선형 대수학 계산에 널리 사용됩니다. 왜냐하면 삼각 행렬을 반전하거나, 행렬식을 계산하거나, 이러한 유형의 행렬을 사용하여 선형 방정식 시스템을 푸는 것이 모든 위치에서 0이 아닌 요소를 갖는 행렬을 사용하는 것보다 훨씬 쉽기 때문입니다. .

상부 삼각 행렬

상부 삼각 행렬은 주대각선 아래의 요소가 0인 정사각 행렬입니다.

상부 삼각 행렬의 예:

하부 삼각 행렬

하부 삼각 행렬은 주대각선 위에 있는 각 요소가 0인 정사각 행렬입니다.

하부 삼각 행렬의 예:

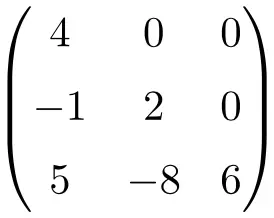
때때로 이러한 행렬은 상부 삼각 행렬의 경우 문자 U로, 하부 삼각 행렬의 경우 문자 L로도 호출됩니다. 이 명명법은 주로 영어로 사용되지만 실제로 U는 상부 삼각행렬 , L은 하부삼각행렬을 의미합니다.

삼각 행렬의 예

2 × 2차원 삼각행렬

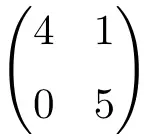
3×3 차 삼각행렬

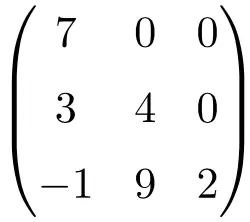
4×4 크기의 삼각 행렬

삼각 행렬의 행렬식

삼각 행렬 의 행렬식은 상부 삼각이든 하부 삼각이든 주대각선 요소의 곱입니다.

행렬식을 찾기 위해 삼각 행렬의 주대각선 요소의 곱셈을 계산하는 것이 어떻게 충분한지 해결한 다음 연습을 살펴보십시오.

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

이 정리는 쉽게 설명됩니다. 블록(또는 보조 인자)을 사용하여 삼각 행렬의 행렬식을 계산하면 됩니다. 이 데모는 일반적인 삼각 행렬을 사용하여 아래에 자세히 설명되어 있습니다.

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

반면, 행렬식이 0과 다르면 행렬이 가역적이라는 것을 우리는 알고 있습니다. 따라서 주대각선에 0이 아닌 요소가 있으면 삼각행렬도 가역성이 되며 결과적으로 정규 행렬이 됩니다. 행렬.

삼각행렬의 속성

이제 삼각행렬의 속성이 무엇인지 살펴보겠습니다.

두 개의 상부 삼각 행렬의 곱은 하나의 상부 삼각 행렬과 같습니다. 그리고 그 반대도 마찬가지입니다. 두 개의 하부 삼각 행렬을 곱하면 또 다른 하부 삼각 행렬이 생성됩니다.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

상부 삼각 행렬의 전치 는 하부 삼각 행렬이고, 그 반대도 마찬가지입니다. 하부 삼각 행렬의 전치는 상부 삼각 행렬입니다.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

삼각 행렬은 주대각선의 모든 요소가 0이 아닌 경우, 즉 0과 다른 경우 역행렬이 가능합니다 . 이러한 경우에는 상(하)삼각행렬의 역행렬도 상(하)삼각행렬이 됩니다.

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

또한 역행렬의 주대각선에는 항상 원래 삼각행렬의 주대각선 요소의 역수가 포함됩니다.

모든 대각 행렬은 상부 삼각 행렬과 하부 삼각 행렬입니다. 예를 들면 다음과 같습니다.

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

따라서 스칼라 행렬은 상삼각행렬과 하삼각행렬이기도 합니다. 예를 들어 단위 행렬은 다음과 같습니다.

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

분명히 영행렬은 주대각선 위와 아래의 요소가 0이기 때문에 상하삼각행렬이기도 합니다.

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

삼각행렬의 고유값(또는 고유값)은 주대각선의 요소입니다.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

상삼각행렬이나 하삼각행렬은 항상 고유벡터(또는 고유벡터)를 기준으로 대각화할 수 있습니다 .

모든 행렬은 하삼각행렬과 상삼각행렬의 곱으로 인수분해될 수 있습니다 . 즉, 모든 행렬은 삼각 행렬 곱셈으로 변환될 수 있습니다. 게다가 행렬이 가역적이라면 이 변환은 고유합니다. 행렬을 인수분해하기 위해 LU 분해 방법이 자주 사용됩니다.

행렬 삼각화

밑변을 변경하여 삼각화할 수 있는 행렬에 대한 몇 가지 정리가 있습니다. 그러나 여기서는 가우스 방법에서와 같이 선에 기본 변환을 적용하여 행렬을 삼각측량하는 방법을 살펴보겠습니다.

예를 들어:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

그리고 이런 방식으로 우리는 이미 원본 행렬을 삼각화했습니다.

가우스 방법에서 라인 사이에 승인된 기본 변환은 다음과 같습니다.

선을 다른 선의 선형 조합으로 바꿉니다.
행의 모든 항에 0이 아닌 숫자를 곱하거나 나눕니다.
주문 라인을 편집합니다.

헤센베르크 행렬

헤센베르크 행렬의 정의는 다음과 같습니다.

헤센베르크 행렬은 “거의” 삼각 행렬입니다. 즉, 첫 번째 하대각선(상부 헤센베르크 행렬) 또는 첫 번째 상대각선(하부 헤센베르크 행렬)부터 시작하여 모든 요소가 0입니다.

상위 Hessenberg 행렬 예제와 또 다른 하위 Hessenberg 행렬 예제를 통해 가장 잘 이해될 수 있다고 확신합니다.

상부 헤센베르크 행렬

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

하부 헤센베르크 행렬

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

상부 및 하부 헤센베르크 행렬인 행렬은 삼중대각 행렬 입니다.

이 행렬은 20세기 독일의 저명한 엔지니어이자 수학자인 칼 헤센베르크(Karl Hessenberg)의 이름을 따서 명명되었습니다.

마지막으로 이러한 유형의 행렬은 삼각 행렬을 곱하면 결과가 항상 헤센베르크 행렬이 된다는 특징이 있습니다.