뺄셈의 미분

9월 17, 2023

이 글에서는 함수의 뺄셈(공식)을 도출하는 방법을 설명합니다. 또한 뺄셈 미분의 예와 연습할 수 있는 단계별 연습 문제도 찾아볼 수 있습니다.

뺄셈의 미분 공식

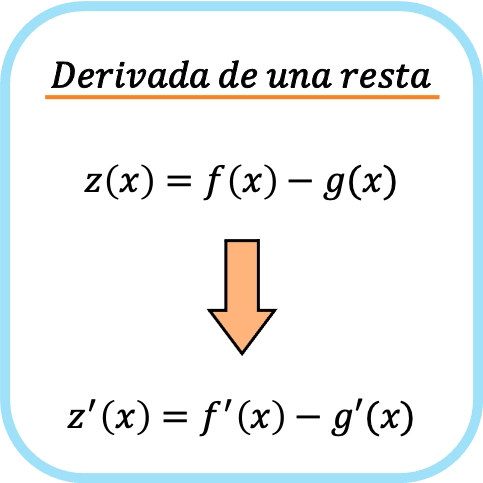
두 함수를 뺀 도함수는 각 함수의 도함수를 따로 빼는 것과 같습니다.

$z(x)=f(x)-g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)-g'(x)$

즉, 두 함수를 따로 미분한 후 빼는 것은 먼저 함수를 빼고 도함수를 취하는 것과 같습니다.

뺄셈의 미분

마찬가지로, 두 개 이상의 함수의 뺄셈에도 동일한 미분 규칙이 적용됩니다. 따라서 3, 4, 5,… 함수의 뺄셈이 있는 경우 각각을 개별적으로 미분한 다음 뺄셈을 해야 합니다.

$\begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}$

보시다시피, 함수 차이의 도함수에 대한 공식은 합계의 도함수에 대한 규칙과 매우 유사합니다.

➤ 참조: 함수 합의 도함수

뺄셈의 미분 예

뺄셈의 도함수 공식이 무엇인지 살펴보았으면 이제 함수의 뺄셈이 어떻게 도출되는지 완전히 이해하기 위해 이러한 유형의 연산에 대한 여러 도함수 예를 분석하는 단계로 넘어갑니다.

예 1: 잠재적인 함수의 뺄셈의 파생

$f(x)=x^3-4x$

두 함수를 뺀 도함수는 각 함수의 도함수 차이를 개별적으로 계산한 것과 동일합니다. 따라서 먼저 각 함수의 도함수를 개별적으로 계산합니다.

$\cfrac{d}{dx} \ x^3=3x^2$

$\cfrac{d}{dx}\ 4x=4$

따라서 전체 함수의 미분은 다음과 같습니다.

$f'(x)=3x^2-4$

예 2: 다양한 함수의 뺄셈의 파생

$f(x)=\text{cos}(x)-\log_7(x^2)$

뺄셈 함수를 미분하려면 먼저 두 함수를 별도로 미분한 다음 빼야 합니다.

$\cfrac{d}{dx} \ \text{cos}(x)=-\text{sen}(x)$

$\cfrac{d}{dx}\ \log_7 (x^2)=\cfrac{2x}{x^2\cdot \ln(7)}=\cfrac{2}{x\ln(7)}$

그리고 두 도함수를 만든 후 동일한 초기 차수로 이를 뺍니다.

$f'(x)=-\text{sen}(x)-\cfrac{2}{x\ln(7)}$

예 3: 제곱 빼기의 파생

$f(x)=\left(x^7-2x^3-9\right)^2$

이 경우에는 세 개의 제곱 함수 사이의 뺄셈이기 때문에 복합 함수가 있습니다. 따라서 전체 함수의 도함수를 계산하려면 잠재적 함수의 도함수에 대한 공식과 연쇄 법칙을 사용해야 합니다.

$f(x)=2\left(x^7-2x^3-9\right)\cdot \left(7x^6-6x^2\right)$

➤ 참고: 거듭제곱의 미분 공식

뺄셈의 미분에 대한 해결 연습

다음과 같은 함수의 뺄셈을 도출합니다.

$\text{A) } f(x)=9x^3-5x$

$\text{B) } f(x)=4x^5-6x^4-x^2-4$

$\text{C) } f(x)=\left(-3x^7-2x^5\right)^4$

$\text{D) } f(x)=\ln(5x^2+3x)-\text{cos}(x)$

$\text{E) } f(x)=8x^3-e^{5x}-\sqrt{8x+2}$

솔루션 보기

$\text{A) } f'(x)=27x^2-5$

$\text{B) } f'(x)=20x^4-24x^3-2x$

$\text{C) } f'(x)=4\left(-3x^7-2x^5\right)^3\cdot (-21x^6-10x^4)$

$\text{D) } f'(x)=\cfrac{10x+3}{5x^2+3x}-\bilg(-\text{sen}(x)\bigr)=\cfrac{10x+3}{5x^2+3x}+\text{sen}(x)$

$\text{E) } f'(x)=24x^2-5e^{5x}-\cfrac{8}{2\sqrt{8x+2}}=24x^2-5e^{5x}-\cfrac{4}{\sqrt{8x+2}}$

뺄셈의 미분 증명

다음으로, 도함수 정의에서 함수 빼기의 도함수 공식을 보여드리겠습니다.

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

따라서 z가 두 가지 다른 함수의 차이인 경우:

$z(x)=f(x)-g(x)$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{z(x+h)-z(x)}{h}$

극한 표현식에서 함수를 빼서 z를 대체합니다.

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)-g(x+h)\bigr]-\bigl[f(x)-g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-g(x+h)-f(x)+g(x)}{h}$

이제 분수를 분리하고 두 분수의 뺄셈을 얻기 위해 변환을 수행하겠습니다.

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}+\frac{-g(x+h)+g(x)}{h}\right]$

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}-\frac{g(x+h)-g(x)}{h}\right]$

극한의 법칙을 적용함으로써 위의 표현을 두 개의 서로 다른 극한으로 분리할 수 있습니다. 뺄셈의 극한은 극한의 뺄셈과 동일하기 때문에:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}-\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

자세히 살펴보면 각 극한은 함수의 도함수에 해당합니다. 이는 차이의 도함수 공식이 충족된다는 의미입니다.

$\displaystyle z'(x)=f'(x)-g'(x)$

댓글 달기 댓글 취소