여기에서는 어떤 유형의 불연속성이 존재하는지 알아볼 수 있습니다. 또한, 모든 유형의 불연속성에 대한 예를 볼 수 있으며, 함수의 불연속 유형에 대한 연습문제를 풀어 연습할 수 있습니다.
모든 유형의 불연속은 무엇입니까?
불연속에는 세 가지 유형이 있습니다.
- 피할 수 있는 불연속성 : 한 점에서 함수의 측면 극한이 함수 값과 일치하지 않습니다.
- 불가피한 유한 점프 불연속성 : 한 점에서 함수의 측면 한계가 다릅니다.
- 불가피한 무한 점프 불연속성 : 함수의 측면 한계 중 하나가 무한대를 제공하거나 존재하지 않습니다.
개념 이해를 마무리하기 위해 각 불연속 유형을 더 자세히 설명하고 세 가지 유형의 불연속을 사용한 함수의 예를 살펴보겠습니다.
피할 수 있는 불연속성
회피가능한 불연속성은 한 점에 경계가 존재하지만 함수의 값과 일치하지 않거나 함수의 이미지가 존재하지 않는 경우 그 점에서 함수를 갖는 불연속의 한 유형입니다.

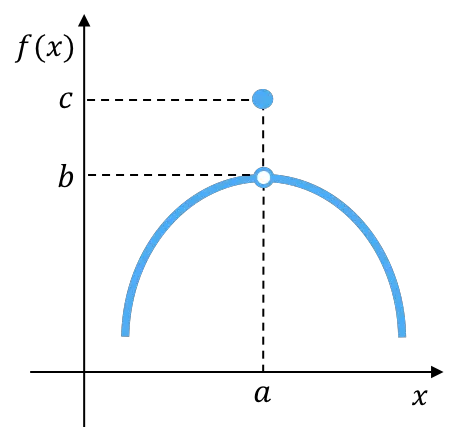
이 함수의 측면 극한은 서로 동일하지만 해당 지점에서의 함수 값과 다릅니다. 따라서 이 함수는 피할 수 있는 불연속성을 나타냅니다.
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5bdc61d377477ddcc788b7230bcfbf_l3.png)
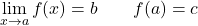
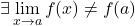

이전 예의 함수는 x=a에서의 측면 한계가 동일한 값을 갖기 때문에 피할 수 있는 불연속성을 가지지만 이 시점에서는 함수의 이미지가 존재하지 않습니다.
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5bdc61d377477ddcc788b7230bcfbf_l3.png)
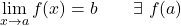
➤ 참조: 함수의 측면 한계
유한 점프의 불가피한 불연속성
불가피한 유한 점프 불연속성은 해당 지점에서 함수의 측면 한계가 동일하지 않을 때 해당 지점에서 함수를 나타내는 불연속 유형입니다.
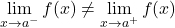
예를 들어, 정의 변경 지점에서 다음 조각으로 정의된 함수의 측면 한계가 다르기 때문에 함수는 해당 지점에서 불가피한 유한 점프 불연속성을 갖습니다.
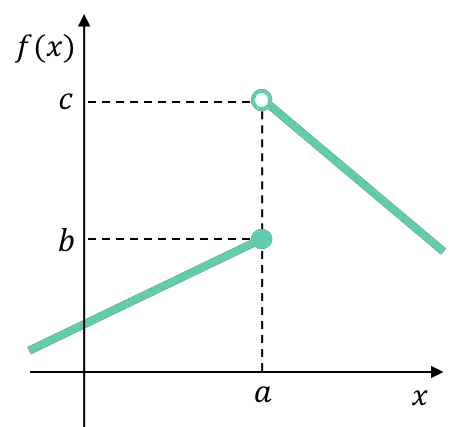

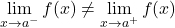
이러한 유형의 불연속성은 일반적으로 조각별(또는 조각별)로 정의된 함수에 나타납니다.
➤ 참조: 조각별 함수의 연속성
무한 점프 불가피한 불연속성
피할 수 없는 무한 점프 불연속성은 그 지점에서 측방한계 중 하나가 무한하거나 존재하지 않을 때 기능을 하는 불연속의 일종이다.

다음 함수의 왼쪽 극한은 실수를 제공하지만 오른쪽 극한은 무한대를 제공합니다. 따라서 이 기능은 불가피한 무한 점프 불연속성을 나타냅니다.
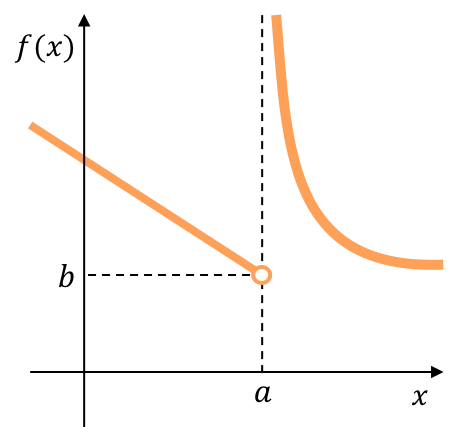
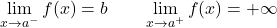
아래에서 두 측면 한계가 무한대를 제공하므로 함수에 불가피한 무한 점프 불연속성이 있는 그래프 함수를 볼 수 있습니다.


이러한 유형의 불연속성은 일반적으로 유리(또는 분수) 함수 에서 발생합니다.
불연속 유형에 대한 해결 연습
연습 1
x=3 지점에서 다음 조각별 함수의 불연속 유형을 결정합니다.
![\displaystyle f(x)= \left\{ \begin{array}{lcl} -2x+1 & \text{si} & x\leq 3 \\[2ex] 4x - 5 & \text{si} & x > 3 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”232″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-8185827ad36ab3921bb96eb5a6da21a9_l3.png)
솔루션 보기
함수의 첫 번째 요소의 영역,
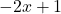
, 두 번째 작품과 마찬가지로
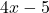
, 다항 함수이기 때문에 모두 실수입니다.
따라서 함수가 불연속적일 수 있는 유일한 지점은 조각별 함수의 중지 지점입니다. 따라서 이 단계에서는 측면 한계를 계산합니다.
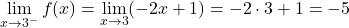
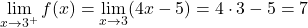
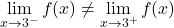
x=3의 두 측면 한계는 서로 다른 결과를 제공합니다. 따라서 x=3 지점은 불가피한 유한 점프 불연속점입니다.
연습 2
다음 유리 함수가 해당 영역에 속하지 않는 점에서 어떤 유형의 불연속성을 나타내는지 찾아보세요.
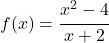
논리적으로 이 연습 문제를 해결하려면 먼저 함수의 영역을 찾아야 합니다. 따라서 이것은 유리함수이므로 분모를 0으로 설정하고 결과 방정식을 풉니다.
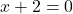
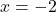
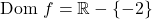
따라서 함수는 x=-2를 제외한 모든 지점에서 연속이므로 x=-2 지점이 어떤 유형의 불연속인지 살펴보겠습니다. 이를 위해 해당 지점에서 함수의 한계를 계산합니다.
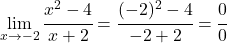
그러나 우리는 0 사이의 불확정성을 0으로 얻으므로 분자와 분모의 다항식을 인수분해하고 단순화합니다.
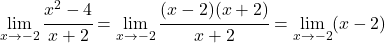
이제 한계를 해결합니다.
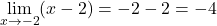
결과적으로, x=-2 지점에서 함수의 극한은 존재하며 -4를 제공합니다. 이제 존재하는지 확인해보자
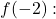
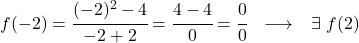
함수의 이미지를 계산할 때 불확정성 0/0은 단순화할 수 없으며 해법도 없습니다. 그래서
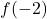
존재하지 않는다.
결론적으로 x=-2에서 함수의 극한은 존재하지만,
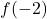
아니요. 따라서 x=-2는 피할 수 있는 불연속입니다.
연습 3
다음 유리 함수의 연속성을 분석합니다.
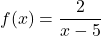
연속함수인지 확인하려면 먼저 정의역을 계산해야 합니다. 따라서 어떤 점이 도메인에 속하지 않는지 확인하기 위해 유리 함수의 분모를 0으로 설정합니다.
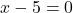
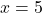
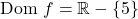
따라서 함수는 x=5를 제외한 모든 점에서 연속입니다. 따라서 이 시점에서 한계를 계산하여 x=5가 어떤 유형의 불연속인지 살펴보겠습니다.
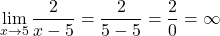
우리는 0으로 나눈 숫자의 불확정성을 발견합니다. 따라서 x=5에서 함수의 측면 한계를 계산합니다.
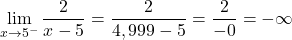
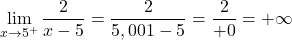
x=5에서 함수의 왼쪽 극한은 마이너스 무한대를 제공하고 오른쪽 극한은 플러스 무한대를 제공합니다. 따라서 함수는 x = 5에서 불가피한 무한 점프 불연속성을 갖습니다. 이 지점에서 적어도 하나의 측면 극한은 무한대 경향이 있기 때문입니다.
연습 4
다음 그래프에 표시된 조각별 함수의 모든 불연속성을 결정합니다.
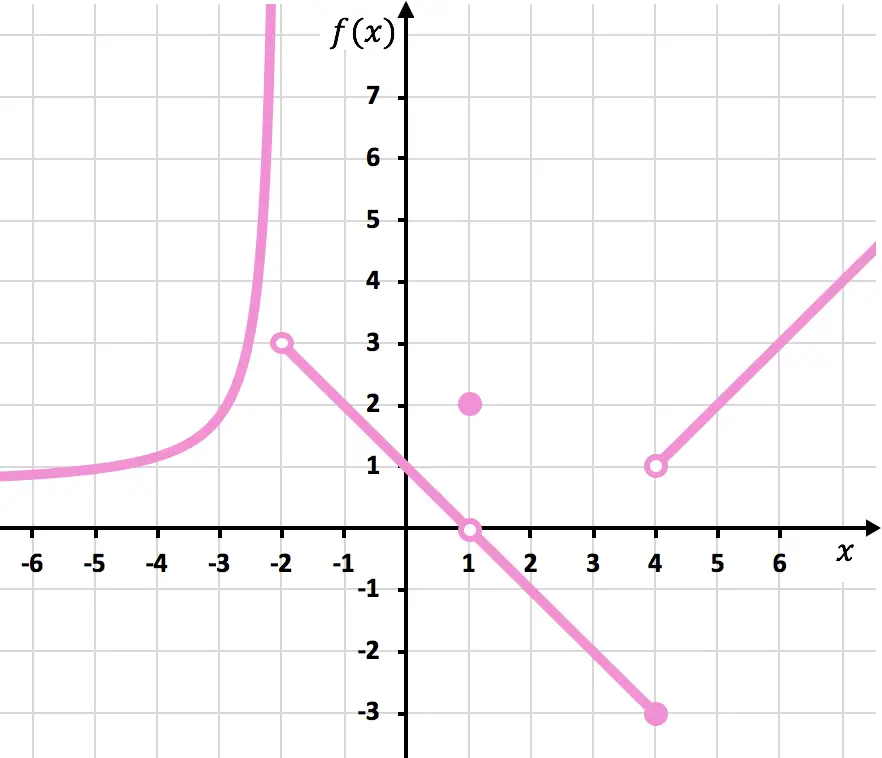
함수를 그리려면 x=-2, x=1, x=4에서 연필을 올려야 합니다. 따라서 함수는 이 세 지점에서 불연속적입니다.
x=-2에서 왼쪽 극한은 +이고 오른쪽 극한은 3입니다. 따라서 측면 극한 중 하나가 무한하기 때문에 함수는 x=-2에서 불가피한 무한 점프 불연속성을 갖습니다.
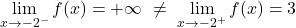
x=1에서 함수의 극한은 0이고, 반면에 x=1에서 함수의 값은 2와 같습니다. 따라서 함수는 x=1에서 피할 수 있는 불연속성을 나타냅니다.
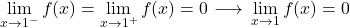
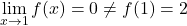
x = 4에서 왼쪽 극한은 -3이고 오른쪽 극한은 1입니다. 따라서 두 측면 극한이 다르고 둘 다 무한대를 제공하지 않으므로 함수는 필연적으로 x =4에서 유한 점프 불연속성을 갖습니다.
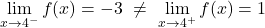
연습 5
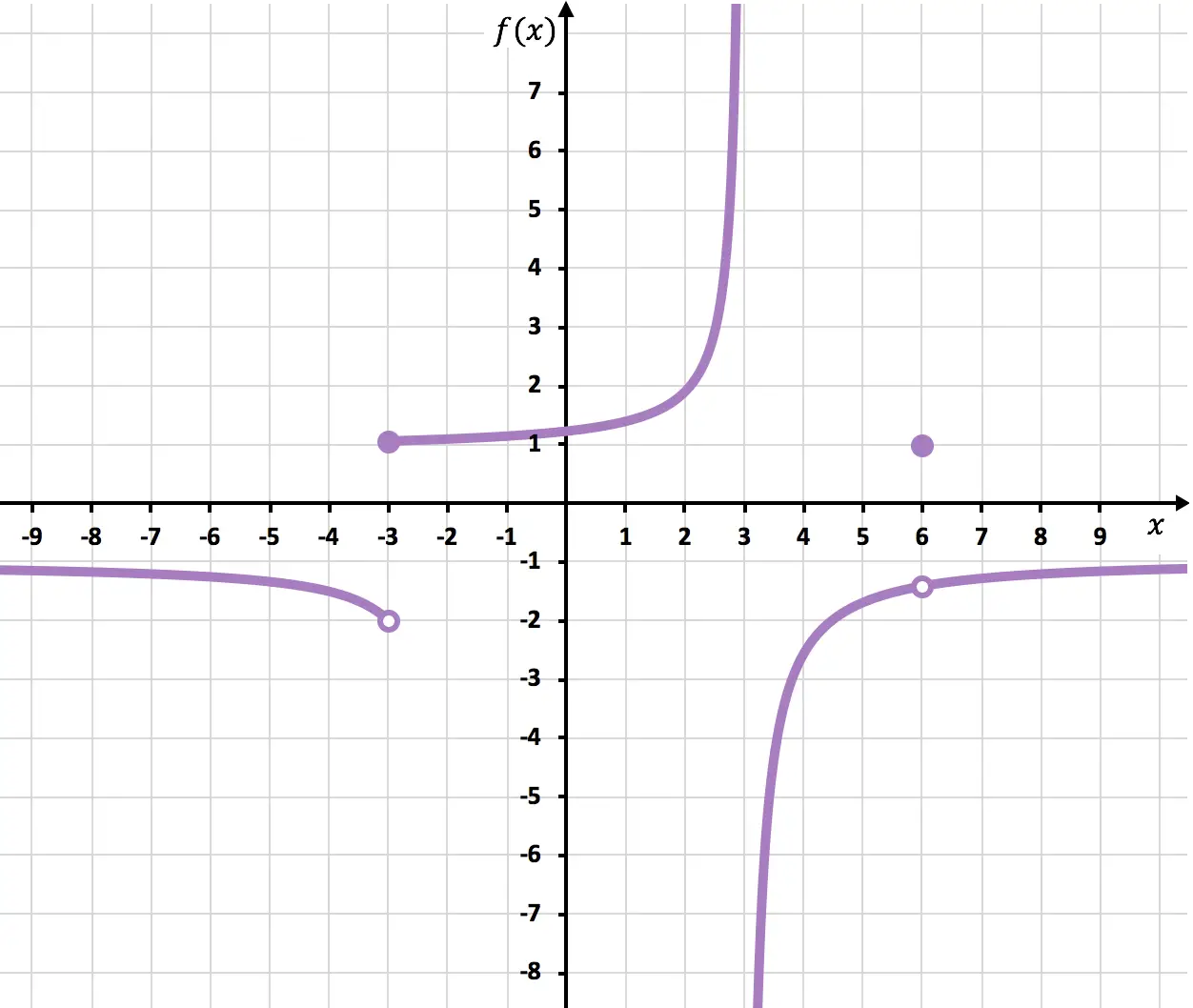
다음 그래프에 표시된 함수의 점근선과 불연속점을 모두 찾아보세요.
점근선
이 함수는 수직선 x=3에 매우 가깝지만 절대 건드리지 않습니다. 또한 x=3에서 왼쪽 측면 극한은 +무한대이고 오른쪽 측면 극한은 -무한대입니다. 따라서 x=3은 수직 점근선입니다.

수평선 y=-1에서도 같은 일이 발생합니다. 함수는 y=-1에 매우 가까워지지만 절대 교차하지 않습니다. 또한 x가 +무한대에 접근하고 -무한대에 접근할 때 함수의 극한은 -1입니다. 따라서 y=-1은 수평 점근선입니다.

불연속
x=6에서는 열린 지점이 있기 때문에 기능이 중단됩니다. x가 6에 접근할 때의 한계는 -1.4이지만 f(6)=1입니다. 따라서 함수는 극한 값이 함수 값과 일치하지 않기 때문에 x=6에서 피할 수 있는 불연속성을 갖습니다.
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4](https://mathority.org/wp-content/ql-cache/quicklatex.com-33612be383c71fea04c8c886710f7f10_l3.png)
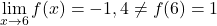
x=-3에서는 측면 한계가 일치하지 않으며 무한대가 제공되지 않습니다. 따라서 이 함수는 x=-3에서 불가피한 유한 점프 불연속성을 갖습니다.
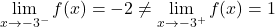
그리고 마지막으로 함수는 x = 3에서 불가피한 무한 점프 불연속성을 갖습니다. 이 지점에서 적어도 하나의 측면 극한이 무한대가 되기 때문입니다.

![]()

![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5bdc61d377477ddcc788b7230bcfbf_l3.png)
![]()
![]()

![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5bdc61d377477ddcc788b7230bcfbf_l3.png)
![]()
![]()

![]()
![]()
![]()

![]()

![]()
![\displaystyle f(x)= \left\{ \begin{array}{lcl} -2x+1 & \text{si} & x\leq 3 \\[2ex] 4x - 5 & \text{si} & x > 3 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”232″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-8185827ad36ab3921bb96eb5a6da21a9_l3.png)


![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4](https://mathority.org/wp-content/ql-cache/quicklatex.com-33612be383c71fea04c8c886710f7f10_l3.png)