복소수는 실수 와 허수 로 구성된 집합입니다. 이 마지막 두 수치 세트는 실제 선과 가상 선을 사용하여 그래픽으로 표현될 수 있습니다. 그리고 두 선을 같은 평면에 배치하면 잘 알려진 복소 평면이 형성됩니다.
복합계획은 무엇인가요?
복소평면은 실수선에 해당하는 실수축(X축)과, 가상선을 개념화하는 허수축(Y축)으로 구성된다.
이 계획에는 모든 복소수가 포함된다는 점에 유의해야 합니다. 따라서 아무리 작거나 작더라도, 복소수를 어떤 형태로 써도 평면상에 그래픽으로 표현할 수 있습니다. 그럼 이 숫자들이 복소 평면에 어떻게 표현되는지 살펴보겠습니다.
복소 평면에 복소수를 그래프로 표시하는 방법은 무엇입니까?
우리가 이미 알고 있듯이 (또는 모르는 경우복소수 에 대한 기사를 읽는 것이 좋습니다) 복소수를 작성하는 방법에는 이항 형식, 극형 및 삼각 형식의 세 가지가 있습니다. 각각은 서로 다른 구조에 따라 복소수 값을 표현하므로 그래픽 표현을 위해 따라야 할 방법이 다릅니다.
다음으로, 세 가지 경우에 따라야 할 절차를 설명합니다.
이항식 표현
가장 일반적인 이항 표기법으로 복소수를 가질 때, 숫자의 구조를 살펴봐야 합니다:

여기서 a는 실수부이고 b는 허수부입니다.
이를 알면 a 값은 가로좌표(실수 축)에 사용되는 값이고 b 값은 컴퓨터(가상 축)에 사용되는 값이라고 추론합니다. 다음 예를 보면 더 잘 이해할 수 있을 것입니다.
우리는 3 + 2i라는 숫자를 표현하려고 노력할 것입니다.
가장 먼저 할 일은 그래프를 그리는 것입니다(가로 축이 실제 축이고 세로 축이 가상 축이라는 점에 유의하세요).

그런 다음 복소수에서 추론한 데카르트 좌표(x, y)에서 그래프의 점을 찾습니다. 이 실제 예에서 우리의 요점은 (3, 2)입니다.
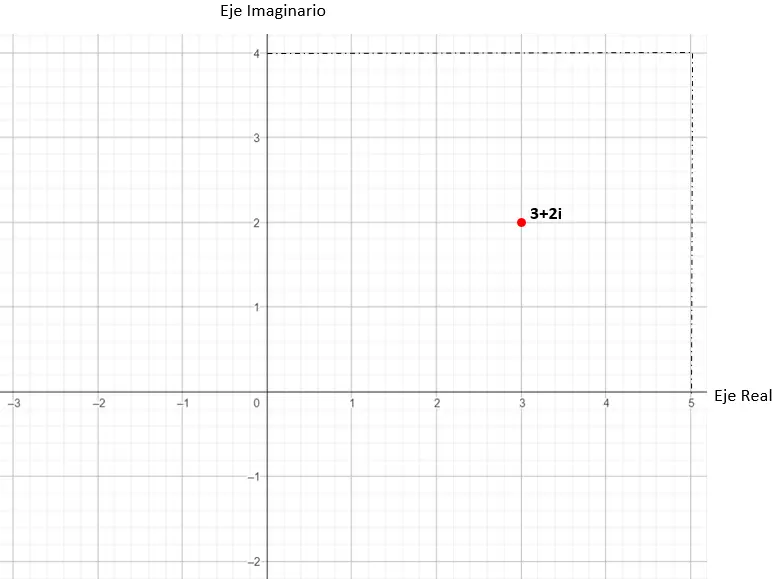
따라서 값 3 + 2i는 복소 평면에 표시됩니다.
극형으로 표현
이제 복소수가 극형으로 어떻게 표현되는지 살펴보겠습니다. 이 방법을 완전히 이해하려면 극 표기법이 모듈과 인수를 기반으로 복소수를 정의한다는 것을 알아야 합니다. 이는 그래픽 표현에서 극좌표(직교 좌표가 아닌!)로 사용됩니다.
그리고 극좌표계의 주요 특징은 점의 위치를 벡터와 각도 로 표현한다는 것입니다(이전 방법과는 다릅니다). 이는 모듈과 복소수의 인수에 해당합니다. 다음으로, 복소수의 극형에 대한 보편식을 보여드리겠습니다.

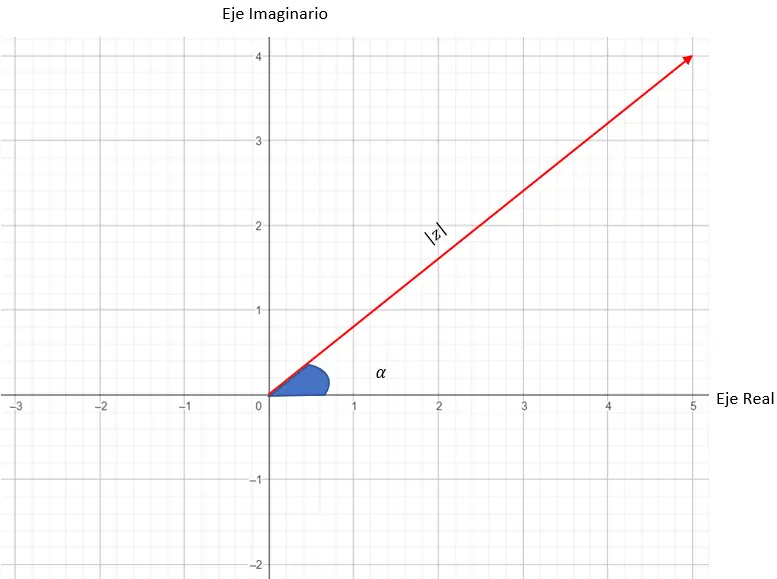
어디 |z| 는 모듈러스이고 α는 인수입니다. 이 두 변수는 계획에서 다음과 같이 변환됩니다.
- 모듈: 벡터를 정의하는 길이입니다(원점과 숫자에 해당하는 점 사이).
- 인수: 벡터가 X축과 이루는 각도입니다.
따라서 복소수의 모듈러스는 그래프를 만드는 데 사용하는 벡터의 길이에 해당합니다. 복소수의 인수 또는 각도는 벡터와 X축 사이의 각도입니다. 아래에서는 모든 변수를 배치하는 다이어그램을 볼 수 있습니다.
이제 우리는 숫자 3 45 를 표현하려고 노력할 것입니다.
먼저 모듈과 인수를 식별해야 합니다.
- 모듈: 3.
- 인수: 45도.
다음으로 그래프에서 모듈러스가 3인 점을 찾아야 합니다. 이 경우 반지름이 3인 원의 모든 점이 작동합니다.
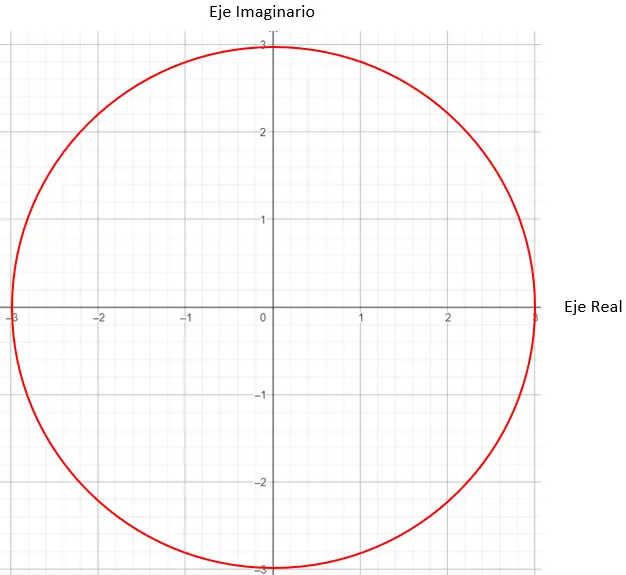
그리고 정확한 지점이 무엇인지 판단을 마치기 위해서는 모듈이 생성한 벡터와 원점이 X축과 45도의 각도를 이루어야 한다는 조건을 넣어야 합니다.
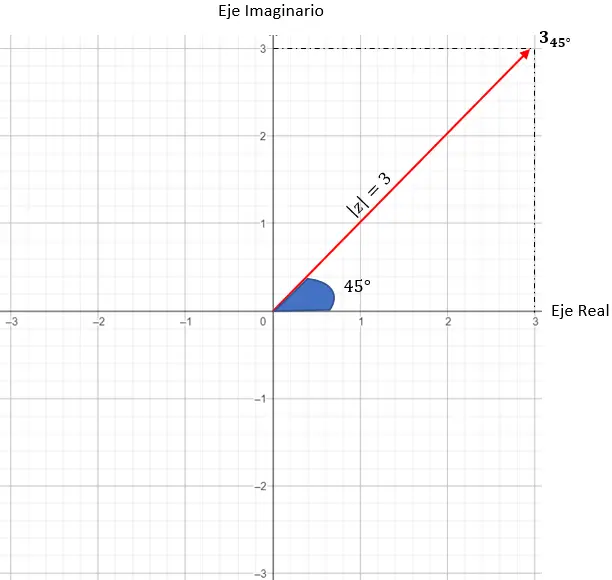
그리고 우리는 이미 극 표기법으로 표현된 복소수를 가지고 있습니다.
삼각법 형태로 표현
마지막으로 복소수가 삼각법 형식으로 어떻게 표현되는지 설명해야 합니다. 이 경우와 이전 경우는 실질적으로 동일합니다. 왜냐하면 극형과 삼각법 형식은 복소수를 표현하기 위해 동일한 데이터(계수와 인수)를 사용하기 때문입니다. 이는 표현식의 구조만 변경합니다.

어디에서, |z| 는 모듈러스이고 α는 인수입니다.
따라서 이전 사례와 동일한 방법을 활용해야 합니다. 모듈을 “길이”로 사용하고 인수를 각도로 사용합니다. 다음 예를 보시면 이해가 더 잘 되실 겁니다.
우리는 z = 4 · (cos(45) + i · sin(45))를 나타낼 것입니다.
가장 먼저 할 일은 모듈과 각도를 식별하는 것입니다.
- 모듈: 4.
- 인수: 45도.
다음으로, 모듈러스가 4인 점을 그래프에서 찾아야 합니다. 이 경우 반지름이 4인 원의 모든 점이 작동합니다.
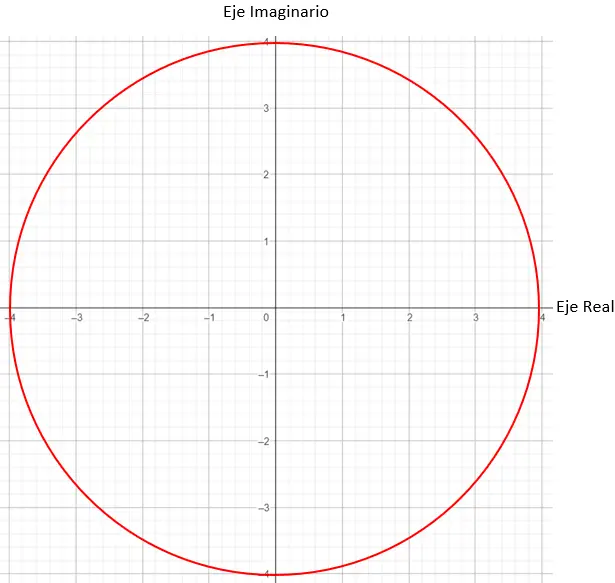
마지막으로 인수에서 알 수 있듯이 모듈러스 벡터와 X축 사이에 형성된 각도가 45도가 되도록 정확한 점을 찾습니다.
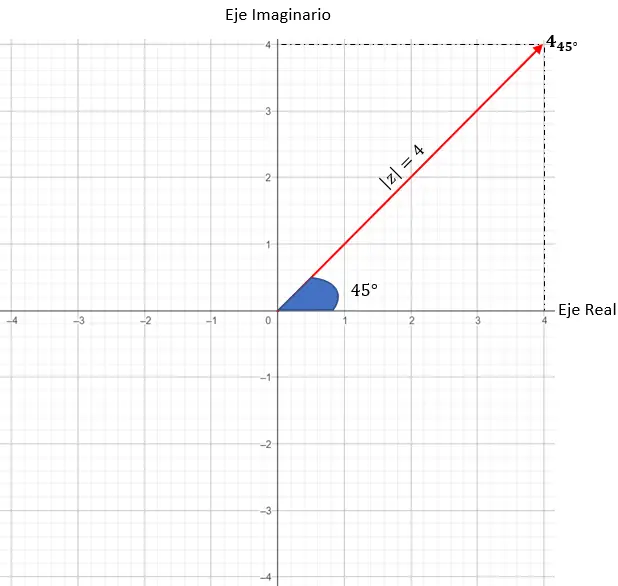
그래서 우리는 삼각법 형태로 복소수를 표현합니다.
복잡한 비행기 운동
이 출판물을 마치기 위해 마지막 연습을 제공하겠습니다. 이 문제를 해결하는 것이 좋습니다. 이렇게 하면 이 문서 전체에 설명된 지식을 통합할 수 있기 때문입니다.
복소 평면에서 다음 세 가지 복소수의 그래픽 표현 증명:
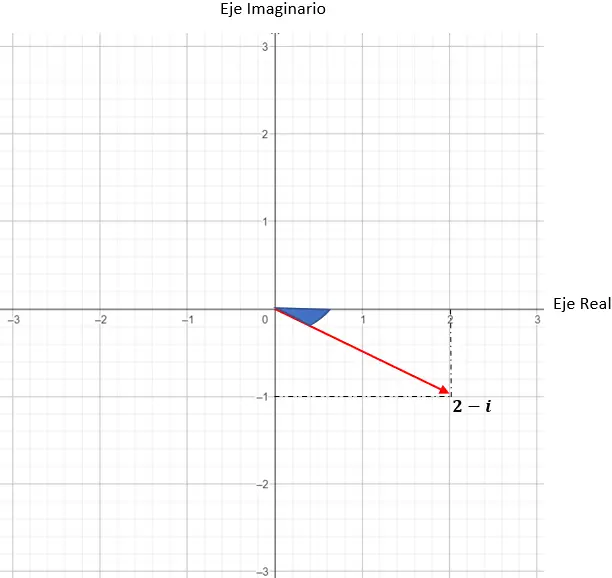
z = 2 – 나는
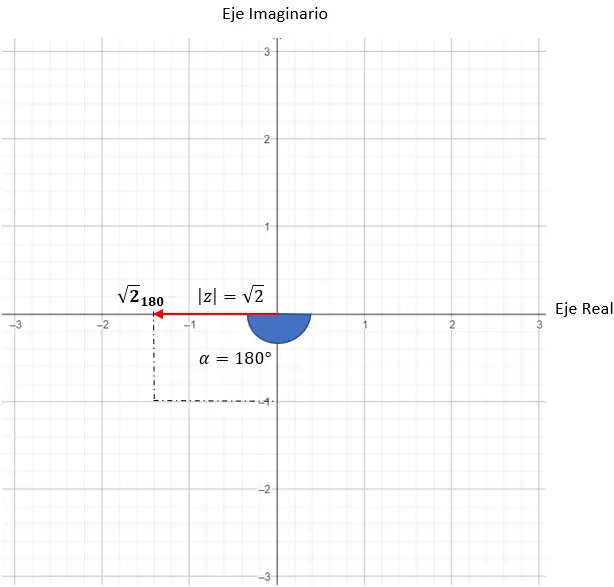
w = √2180
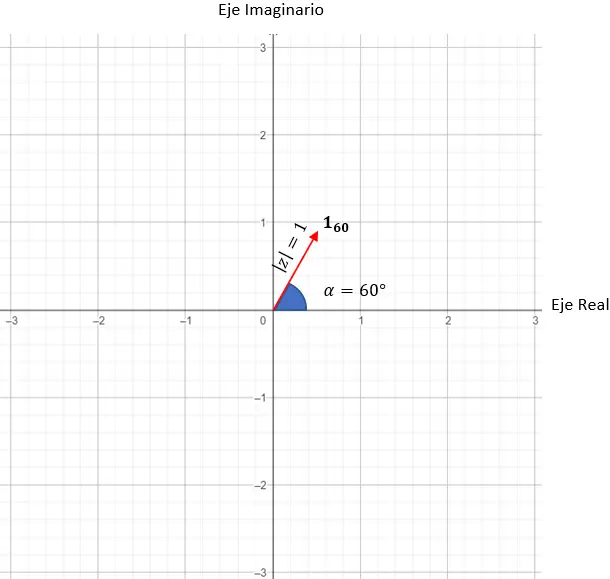
p = cos(60) + 나는 죄(60)
복잡한 계획에 대해 자세히 알아보기
- 복소수
- 허수