복소수, 공액 및 전치 행렬

이 페이지에서는 복소수 행렬, 켤레 행렬, 켤레 전치 행렬이 무엇인지 볼 수 있습니다. 이제 그들은 당신과 매우 비슷해 보이지만 페이지 끝에서 각각의 차이점을 어떻게 완전히 이해하게 될지 알게 될 것입니다. 또한 각 유형과 해당 속성의 예를 살펴보겠습니다.

복소수 행렬

켤레 행렬과 전치 켤레 행렬에 대한 설명을 보기 전에 복소 행렬의 개념을 살펴보겠습니다.

복잡한 행렬이란 무엇입니까?

복소 행렬은 요소 사이에 특정 복소수를 갖는 행렬입니다.

복소수 또는 허수는 실수 부분과 허수 부분으로 구성된 숫자이며 문자 i로 표시됩니다. 예를 들어:

$3+5i$

복잡한 행렬의 예

복잡한 다차원 배열의 몇 가지 예를 살펴보겠습니다.

2 × 2 차 복소 행렬의 예

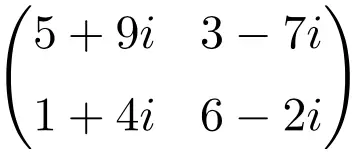
차원 3×3의 복소 행렬의 예

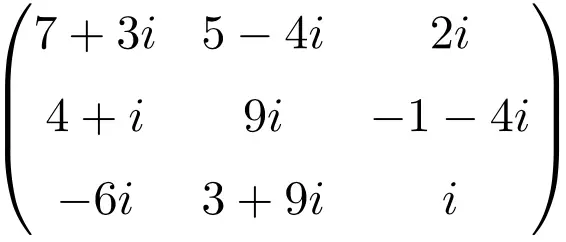
크기가 4×4인 복소 행렬의 예

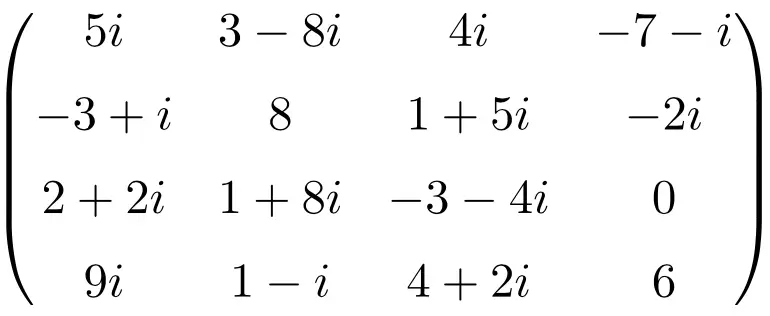
켤레 행렬

복소수 행렬의 정의가 무엇인지 살펴보고 나면 켤레 행렬과 전치 켤레 행렬이 무엇인지 살펴보겠습니다.

켤레 행렬이란 무엇입니까?

켤레 행렬은 모든 요소가 켤레로 대체된 복소 행렬입니다. 즉, 모든 복소수의 허수 부분의 부호가 변경되었습니다.

켤레 행렬

$A$

위의 가로 막대로 표현됩니다.

$\overline{A}$

켤레 행렬의 예

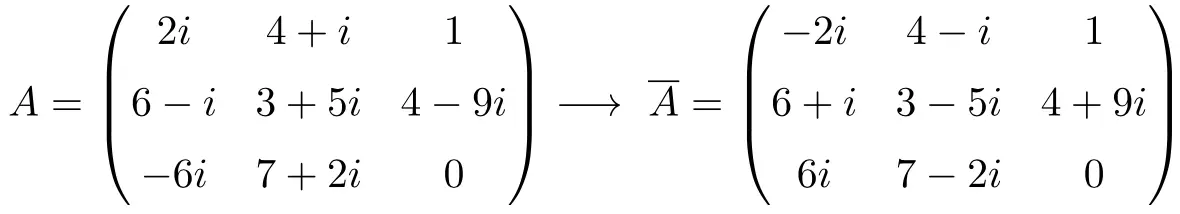
공액 행렬의 속성

이 유형의 매트릭스의 특징은 다음과 같습니다.

켤레 행렬의 켤레는 원래 행렬입니다.

$\displaystyle \overline{\bigl( \ \overline{A} \vphantom{A^{9^1}} \ \bigr)} = A$

두 개의 행렬을 더하거나 빼서 결과를 켤레화하는 것은 먼저 두 행렬을 별도로 켤레화한 다음 이를 더하거나 빼는 것과 같습니다.

$\displaystyle \overline{\bigl( A \pm B \bigr)} = \overline{A} \pm \overline{B}$

두 행렬의 켤레 곱은 두 행렬을 별도로 켤레화한 다음 행렬 곱셈을 계산하는 것과 같습니다.

$\displaystyle \overline{\bigl( A \cdot B \bigr)} = \overline{A} \cdot \overline{B}$

행렬에 스칼라를 곱하고 결과를 켤레화하는 것은 먼저 스칼라와 행렬의 켤레를 수행한 다음 곱을 구하는 것과 같습니다.

$\displaystyle \overline{\bigl( k \cdot A \bigr)} = \overline{k} \cdot \overline{A}$

행렬을 전치한 다음 이를 켤레화한다는 것은 먼저 행렬을 켤레화한 다음 이를 전치한다는 것을 의미합니다.

$\displaystyle \overline{\bigl(A^t \bigr)} = \left( \overline{A}\right)^t$

행렬의 역행렬을 수행한 후 이를 켤레화하는 것은 행렬을 켤레화한 다음 이를 반전시키는 것과 같습니다.

$\displaystyle \overline{\bigl( A^{-1} \bigr)} = \left(\overline{A} \right)^{-1}$

켤레 행렬의 순위는 동일한 비공액 행렬의 순위와 같습니다.

$\displaystyle rg\left(\overline{A}\right) =rg(A)$

공액 행렬의 자취를 계산하는 것과 공액이 없는 동일한 행렬의 자취를 계산한 후 그 결과를 공액시키는 것은 무차별입니다.

$\displaystyle tr\left(\overline{A}\right) =\overline{tr(A)}$

마지막으로, 켤레 행렬의 행렬식을 취하는 것은 켤레 없는 동일한 행렬의 행렬식 결과의 켤레를 계산하는 양입니다.

$\displaystyle det\left(\overline{A}\right) = \overline{det(A)}$

켤레 전치 행렬

마지막으로, 행렬을 켤레화하는 방법을 살펴본 후 켤레 전치 행렬의 개념으로 넘어가겠습니다.

켤레 전치(또는 전치) 행렬이란 무엇입니까?

전치된(또는 전치된) 공액 행렬은 행렬을 전치한 후 공액을 만든 후에 얻은 것입니다.

이러한 유형의 행렬을 adjoint 행렬 또는 간단히 adjoint 행렬이라고도 합니다. 또한 일반적으로 별표로 표시됩니다.

$(A^*)$

, 비록 다음과 같이 그리는 수학자들이 있지만

$A^*$

어느 하나

$A^H$

켤레 전치 행렬의 예

다음은 행렬의 전치(또는 켤레 전치)를 계산하는 예입니다.

$\displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}$

먼저 행렬 A를 전치합니다.

$\displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}$

그런 다음 전치의 공액 행렬을 계산합니다. 즉, 모든 복소수의 허수부의 부호를 변경합니다.

$\displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}$

따라서 켤레 전치 행렬의 계산을 요약하면 다음과 같습니다.

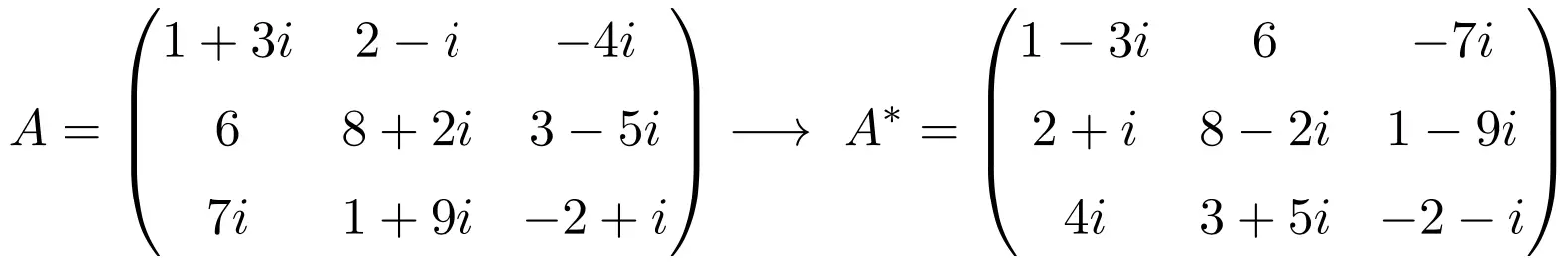
켤레 전치 행렬의 속성

이 유형의 정사각 행렬의 속성은 다음과 같습니다.

이전에 전치되고 공액된 행렬의 공액 전치 행렬이 원래 행렬입니다.

$\displaystyle \bigl(A^*\bigr) ^* = A$

켤레 전치 행렬의 덧셈 속성 에 따르면 두 행렬을 더하거나 뺀 다음 이 연산을 결과에 적용하는 것은 먼저 각 행렬의 켤레 전치를 수행한 다음 결과를 더하거나 빼는 것과 동일합니다.

$\displaystyle \bigl( A\pm B \bigr)^* = A^*\pm B^*$

두 행렬을 곱한 다음 켤레 전치를 수행하면 켤레 전치 행렬의 역곱과 동일한 결과를 얻을 수 있습니다.

$\displaystyle \bigl( A\cdot B \bigr)^* = B^*\cdot A^*$

스칼라와 행렬의 곱의 켤레 전치 행렬을 계산하는 것은 복소수를 켤레화하고 행렬의 켤레 전치를 따로 구한 후 곱하는 것과 같습니다.

$\displaystyle \bigl( k\cdot A \bigr)^* = \overline{k}\cdot A^*$

행렬이 역행렬인 경우 행렬 반전 및 켤레 전치 연산이 수행되는 순서는 관련이 없습니다.

$\displaystyle \bigl( A^{-1} \bigr)^*= \bigl( A^* \bigr)^{-1}$

복소수 행렬

복잡한 행렬이란 무엇입니까?

복잡한 행렬의 예

켤레 행렬

켤레 행렬이란 무엇입니까?

켤레 행렬의 예

공액 행렬의 속성

켤레 전치 행렬

켤레 전치(또는 전치) 행렬이란 무엇입니까?

켤레 전치 행렬의 예

켤레 전치 행렬의 속성

댓글 달기 댓글 취소