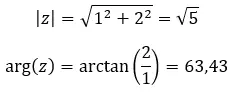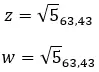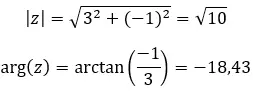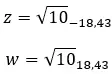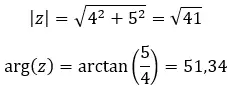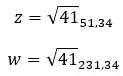이 글에서는 계산을 풀고 표현식을 단순화할 때 유용할 수 있는 복소수의 속성에 대해 설명합니다. 이러한 속성으로 바로 이동해 보겠습니다.
복소수의 모듈러스 및 인수
복소수의 첫 번째 속성은 복소수의 모듈러스와 인수입니다. 몇 가지 수식만 적용하면 되기 때문에 계산이 매우 쉽습니다.
모듈을 계산하는 공식:

인수를 계산하는 공식은 다음과 같습니다.

이제 숫자가 극좌표나 삼각법 형식으로 표현되면 계산할 필요가 없습니다. 왜냐하면 동일한 표현식에는 모듈과 인수가 나열되어 있기 때문입니다.
아래 이미지에서 극좌표 형식의 숫자 공식을 볼 수 있습니다. 여기서 |z| 는 모듈러스이고 α는 인수입니다.

그리고 이 다른 이미지에서는 삼각법 형식으로 표현된 숫자의 구조를 볼 수 있습니다. 여기서 |z| 는 모듈러스이고 α는 인수입니다.

복소수와 같음
동일한 복소수는 모듈러스와 인수를 공유하는 숫자입니다. 따라서 다음 두 값에서 다음을 수행합니다.

이는 다음 속성을 만족하는 경우에도 동일합니다.
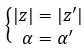
반면에 두 숫자가 모두 이항 형식인 경우 두 숫자가 동일한 복소수인지 확인하기 위해 매우 빠르고 쉽게 확인할 수 있습니다. 간단히 말해서 다음 표현식이 충족되어야 합니다.
a + bi = a + bi
예를 들어 다음 두 복소수가 동일한지 확인해 보겠습니다.
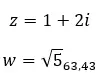
켤레 복소수
이제 복소수의 가장 중요한 속성 중 하나로 넘어가겠습니다. 왜냐하면 복소수의 공액을 계산하는 방법을 아는 것이 복소수 나눗셈을 해결하고 단순화하는 데 많은 도움이 되기 때문입니다.
따라서 다음 두 값에서 다음을 수행합니다.

모듈을 공유하고 반대 주장이 있으면 결합되었다고 말합니다. 따라서 다음 사항을 완료해야 합니다.
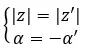
반면에 두 숫자가 모두 이항 형식인 경우 두 개의 복소공액수인지 확인하기 위해 매우 빠르고 쉽게 확인할 수 있습니다. 간단히 말해서 다음 표현식이 충족되어야 합니다.
유엔 + 바이 = 유엔 – 바이
예를 살펴보고 다음 두 복소수가 공액인지 확인하십시오.
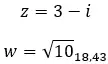
반대 복소수
다음으로 반대 복소수의 성질을 살펴보겠습니다. 이 두 값에서:

동일한 모듈을 가지고 있고 인수가 180도 또는 π 라디안만큼 다른 경우 서로 반대라고 말할 수 있습니다.
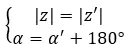
반면에 두 숫자가 모두 이항 형식인 경우 더 빠르고 간단한 또 다른 방법을 사용하여 두 숫자가 반대되는 복소수인지 알아낼 수 있습니다. 간단히 말해서 다음 표현식이 충족되어야 합니다.
a + bi = -a – bi
예를 들어 다음 두 복소수가 반대인지 확인해 보겠습니다.
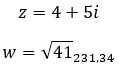
다른 속성
분명히 이 숫자 집합에는 역복소수 및 기본 산술 연산과 직접 관련된 몇 가지 다른 속성과 같은 다른 속성이 있습니다. 이 모든 내용은 다른 기사에서 다루지만 아래 목록에서 볼 수 있습니다.
복소수의 성질에 대해 알아보세요
- 복소수
- 복소수 연산
- 복잡한 뿌리
- 복소수의 그래픽 표현