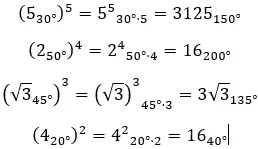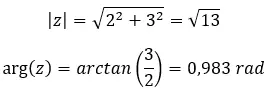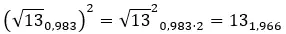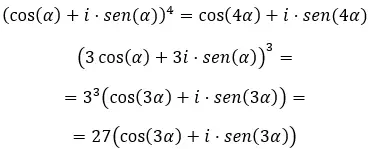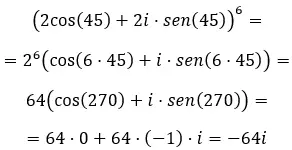올바른 방법을 알고 있다면 복소수의 거듭제곱을 푸는 것은 매우 쉬운 일입니다. 따라서 이 기사에서는 이항 형식, 극좌표 형식 및 삼각법 형식의 복소수에 대해 세 가지 방법으로 복소수를 푸는 방법을 설명합니다.
복소수의 힘을 해결하는 방법은 무엇입니까?
서문에서 말했듯이 복잡한 권한을 사용하면 세 가지 상황이 발생할 수 있습니다. 첫 번째이자 가장 간단한 방법은 극형의 숫자가 주어졌을 때입니다. 두 번째는 이항 형식으로 숫자가 주어졌을 때이고, 세 번째는 삼각법 형식으로 숫자가 주어졌을 때입니다.
즉, 극형의 콤플렉스로 동작시키면 운동을 더욱 빠르게 해결할 수 있다. 따라서 해당 숫자를 극형으로 변환하는 것이 좋습니다. 그러나 실제로 모든 방법은 해결하기 쉽습니다 . 즉, 모든 사건이 어떻게 해결되었는지 설명하고 실습을 제공할 것입니다.
극좌표 형태의 복소수의 거듭제곱
극형의 복소 거듭제곱을 풀고 싶을 때, 모듈러스를 임의의 값으로 올리고 인수에 n을 곱하면 됩니다. 수학적으로 표현하면 다음 공식을 얻습니다.
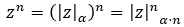
다음은 몇 가지 예입니다. 스스로 해결해 볼 수 있습니다.
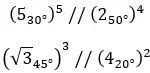
이항 형식의 복소수의 거듭제곱
반면에, 이항 형식의 복소 거듭제곱을 풀고 싶을 때는 두 가지 다른 방법을 사용할 수 있습니다. 첫 번째는 “대수적” 방식(마치 i가 변수인 것처럼 해결)으로 거듭제곱을 해결하는 방법을 다룹니다. 그리고 두 번째 시스템은 이항 형식을 극형으로 변환한 다음 이전 절차를 따르는 것입니다.
이항식에서 극형으로 전환하는 방법을 모른다면복소수에 대한 기사에서 매우 명확하게 설명합니다. 하지만 이제는 예를 통해 빠르게 살펴보겠습니다.
다음 복소수를 풀어보세요: (2 + 3i) 2 .
삼각법 형태의 복소수의 거듭제곱
마지막으로, 삼각법 형식의 복소 거듭제곱을 풀려면 잘 알려진 드 무아브르(de Moivre) 공식을 사용해야 합니다. 다음과 같이 작성되었습니다.
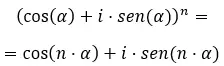
이 공식을 알고 다음 연습문제를 풀어보세요.

복잡한 힘에 대해 자세히 알아보기
- 복소수
- 단지의 속성
- 복소수 연산
- 복잡한 뿌리