아마도 복소수(complex number) 라는 말을 들어보셨을 것입니다. 실수와 허수를 결합하기 때문에 아마도 가장 다루기 어려운 숫자 집합일 것입니다. 이를 통합하면 모든 실수를 사용하여 처리할 수 없는 수치적 동작을 연구할 수 있습니다.
복소수란 무엇입니까?
복소수는 실수 와 허수 의 조합입니다. 예를 들어, 4 + 5i 는 실수부가 4이고 허수가 5i인 복소수입니다. 일반적으로 다음 공식으로 표현할 수 있습니다.
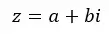
여기서 Re(z) = a이고 Im(z) = b입니다.
우리가 잘 말했듯이, 복소수는 실수와 허수를 모두 포함하는 가장 큰 집합 또는 전역 집합 입니다. 다음으로 모든 세트의 계층 구조에 대한 작은 다이어그램을 보여줍니다.

따라서 실수와 허수를 조합하면 복소수가 됩니다. 그러나 두 부분 중 하나가 0인 경우가 있습니다. 이런 경우에는 어떻게 되나요? 음, 우리는 여전히 복소수를 다루고 있습니다. 왜냐하면 복소수 집합은 다른 모든 숫자 집합을 포함하기 때문입니다. 그러나 우리는 다른 하위 범주를 입력합니다.
| 복소수 | 왕실 파티 | 상상력 부분 | 하위 카테고리 |
| 2+5i | 2 | 5i | 복잡한 |
| 4 | 4 | 0 | 순수한 왕실 |
| 3i | 0 | 3i | 순수한 상상력 |
순수 실수가 있을 때 허수값 b가 0과 같으므로 나머지 복소수는 다음과 같습니다.
z = a + 0i = a
반면에, 우리가 순수한 상상을 할 때, a는 0과 같고 결과적으로 복소수는 다음과 같이 유지됩니다:
z = 0 + bi = bi
복소수의 그래픽 표현
복소수를 표현하기 위해 복소 평면 을 사용합니다. 실제 직선과 가상 직선이라는 두 개의 직선 으로 구성됩니다. 이 두 수직선은 각 세트의 숫자를 그래픽으로 찾는 데 사용되며, 이를 합치면 다음과 같은 계획을 얻을 수 있습니다.

X축은 실제 부품 값이 위치하는 곳이기 때문에 실제 축이라고 합니다. Y축을 허수축이라고 부르는데, 여기에 허수값이 쓰여집니다. 예를 들어, 복소 평면에 숫자 3 + 2i 를 배치하겠습니다.

이미지에서 볼 수 있듯이 숫자 3과 2를 각각 축에 대한 좌표로 사용하여 숫자를 찾았습니다. 복소수 표현에 대해 더 자세히 알고 싶다면 이 글을 읽어 보시기 바랍니다.
복소수의 유형은 무엇입니까?
이제 우리는 복소수를 표현하는 방법을 살펴보겠습니다. 지금까지 우리는 실수 부분과 허수 부분의 합으로 표현되는 기본 형식(이항 형식이라고 함)만 살펴보았습니다.
그러나 실제로는 이항형, 극형, 삼각형 의 세 가지 형태가 있습니다. 각 표현 유형에는 고유한 속성이 있으며 상황에 따라 사용됩니다. 그래서 우리는 그것들을 모두 설명하고 하나에서 다른 것으로 이동하는 방법을 보여줄 것입니다.
1. 이항형
이항 형식 의 복소수는 실수부와 허수부의 합(a + bi)으로 작성됩니다. 예를 들어 숫자 6 + i는 이항 표기법으로 표현되는 복소수입니다. 이 경우 공식은 항상 동일합니다.

따라서 복소수를 이항 형식으로 표현하려면 그 실수값과 허수값만 알면 됩니다.
예를 들어, 값 3 + 2i 는 이항 형식이며 이전에 본 것처럼 다음과 같이 표현됩니다.

이항 형식은 복소수의 덧셈과 뺄셈을 푸는 데 주로 사용됩니다.
2. 극형
복소수를 극형 으로 표현하려면 해당 모듈 |z|를 계산해야 합니다. 그리고 그의 주장. 극형은 복소수의 곱셈과 나눗셈을 풀어야 할 때 주로 사용됩니다.
복소수의 모듈러스를 계산 하려면 다음 공식에 설명된 대로 a와 b의 모듈러스를 계산하면 됩니다.

그리고 z의 인수나 각도를 계산 하려면 a 사이의 b의 아크탄젠트를 계산해야 합니다.

각도 α의 값을 정확히 결정하려면 해당 각도가 어느 사분면에 있는지 식별해야 한다는 점에 유의하는 것이 중요합니다. 실제로 아크탄젠트 함수는 π/2와 -π/2 사이의 각도만 계산합니다. 복소수가 어느 사분면에 있는지 지정하려면 a와 b 값을 살펴봐야 합니다(양수인지 음수인지).
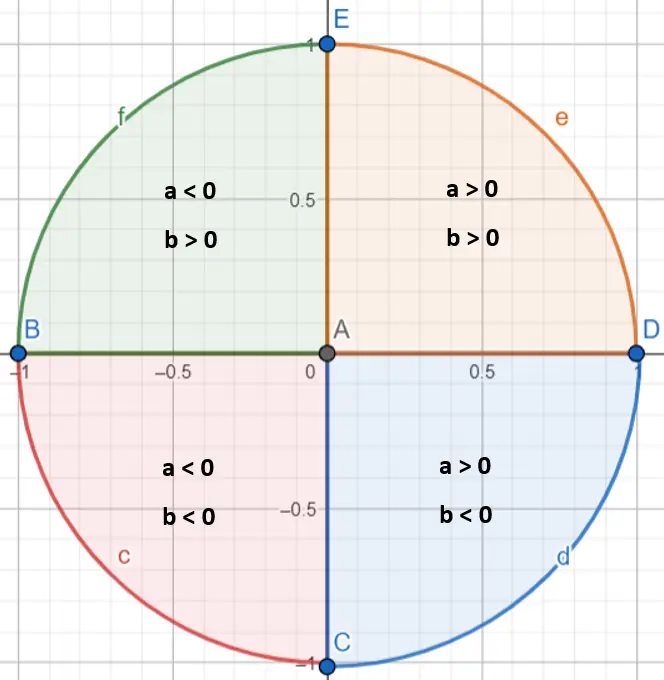
숫자가 어느 사분면에 속하는지 알고 나면 몇 가지 규칙을 따라야 합니다.
- 복소수가 첫 번째 사분면(a > 0 및 b > 0)에 있으면 인수를 그대로 둡니다.
- 복소수가 두 번째 사분면(a < 0 및 b > 0)에 있으면 인수에 π를 추가합니다.
- 복소수가 세 번째 사분면(a < 0 및 b < 0)에 있으면 인수에서 π를 뺍니다.
- 복소수가 네 번째 사분면(a > 0 및 b < 0)에 있으면 인수에 2π를 추가합니다.
사분면이라고 할 때 무엇을 말하는지 모르는 경우 삼각비 에 대한 기사를 참조하는 것이 좋습니다.
z의 크기와 인수를 알면 복소수를 극형으로 표현할 수 있습니다. 이 형식은 여러 명명법을 허용하지만 두 가지 주요 명명법은 다음과 같습니다.

예를 들어 숫자 3 + 5i 를 극좌표로 변경하려면 다음 절차를 따르면 됩니다.
먼저 모듈을 계산합니다.
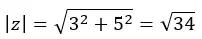
그런 다음 첫 번째 사분면에 있는 인수를 계산하므로 계산한 대로 유지됩니다.
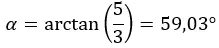
그리고 우리는 숫자를 극형으로 표현합니다.
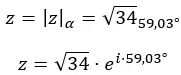
그래픽 표현은 다음과 같습니다.
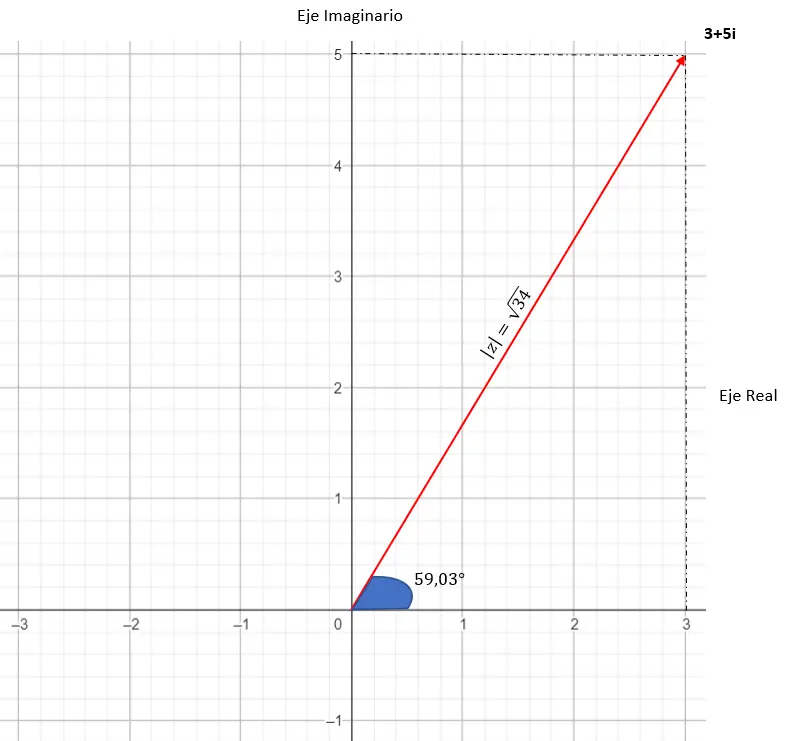
3. 삼각법 형태
마지막으로 오일러 공식 으로 계산되는 삼각법 표기법이 있습니다.

예를 들어 숫자 4 – 3i를 삼각함수 형태로 표현하려면 다음 절차를 따릅니다.
극좌표 형식 섹션에서 사용한 공식을 사용하여 계수와 인수를 계산하는 것부터 시작합니다.
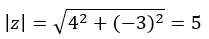
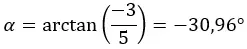
주의: 인수는 (a > 0 및 b < 0)이기 때문에 네 번째 사분면에 있습니다.
데이터를 삼각법 형식으로 방정식에 추가합니다.
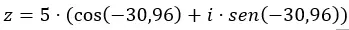
그리고 우리는 이미 삼각법 형태로 표현된 숫자를 가지고 있습니다. 그래픽 표현은 다음과 같습니다.
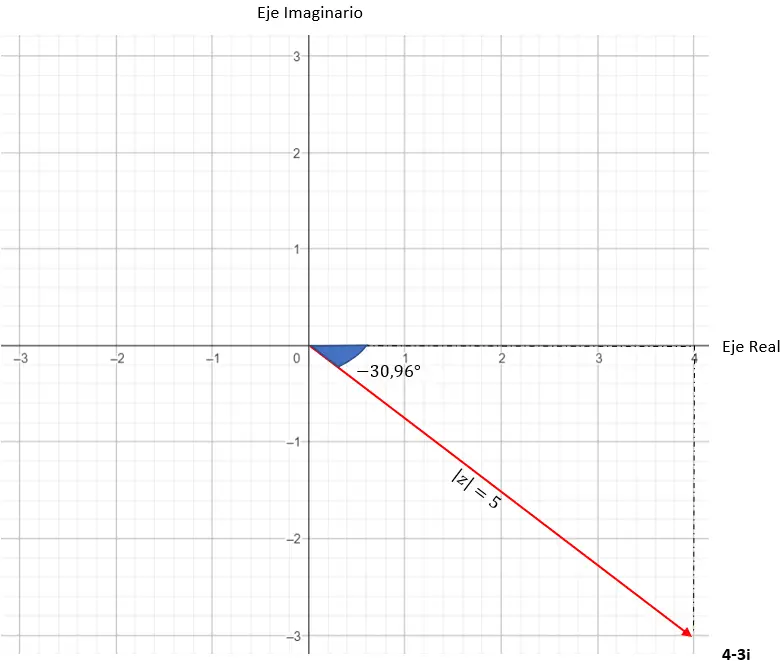
한 유형에서 다른 유형으로 전환하는 방법은 무엇입니까?
이제 당신은 복소수를 표현하는 모든 방법을 알았습니다. 마지막 섹션 전체에서 각 양식에 액세스하는 방법을 볼 수 있었지만 마치기 전에 한 양식에서 다른 양식으로 이동하는 방법에 대한 간단한 요약을 제공하고 싶습니다. 이전 섹션에서 본 수식 만 사용하면 됩니다.
이항형에서 극형으로 또는 그 반대로
이항에서 극으로 이동하기 위해 다음 다이어그램을 제안합니다.
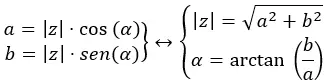
앞서 이항에서 극항으로 이동하는 예를 보았으므로 이제 위 다이어그램을 사용하여 극항에서 이항으로 이동하겠습니다. √41 38.66을 이항식으로 변환해야 합니다.
먼저 a를 계산합니다.
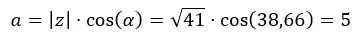
그런 다음 b를 계산합니다.
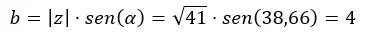
그리고 이를 이항식으로 표현합니다.
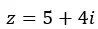
이 숫자의 그래픽 표현은 다음과 같습니다.
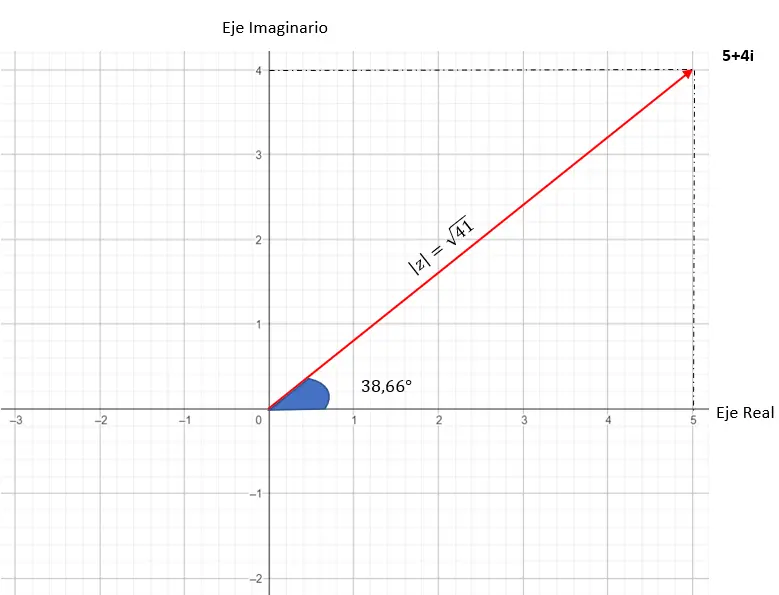
이항 형식에서 삼각 형식으로 또는 그 반대로
이항식에서 삼각법으로 이동하려면 이전 섹션에서 설명한 공식도 적용해야 합니다. 이러한 방식으로 먼저 모듈러스와 인수를 계산한 다음 이 데이터를 삼각법 형식의 방정식에 넣습니다. 예를 들어 숫자 z = 3 + 2i를 삼각법으로 전달하겠습니다.
먼저 모듈러스와 인수를 계산합니다.
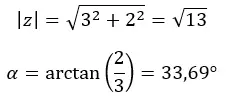
주의: (a > 0 및 b > 0) 때문에 인수는 첫 번째 사분면에 있습니다.
그런 다음 이 데이터를 사용하여 삼각함수 방정식을 완성합니다.
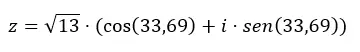
그리고 삼각법에서 이항법으로 가고 싶다면, 우리가 해야 할 일은 이전 식을 푸는 것뿐입니다.
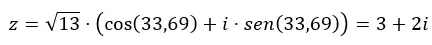
극형에서 삼각법 형태로 또는 그 반대로
마지막으로 극좌표 형식에서 삼각법 형식으로 이동하겠습니다. 이는 매우 간단합니다. 이 두 형식은 모듈로(modulo)와 인수(argument) 라는 동일한 두 값으로 표현되기 때문입니다. 따라서 양식을 작성하기만 하면 됩니다.
예를 들어 숫자 z = √85 12.53 을 삼각법 형식으로 변환하겠습니다.
삼각법 형식의 방정식에서 두 변수(모듈과 인수)를 재구성합니다.
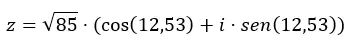
이제 한 형태에서 다른 형태로 전환하는 방법을 알았으니 몇 가지 연습을 통해 조금씩 연습해 보는 것이 좋습니다. 이렇게 하면 이 기사에서 배운 지식을 통합할 수 있습니다. 이 주제와 관련하여 질문이 있으시면 언제든지 댓글에 남겨주세요. 그리고 복소수에 대해 더 자세히 알고 싶다면 아래 링크를 확인하세요.
복소수에 대한 추가 정보
- 허수
- 복소수의 속성
- 복소수 연산
- 복소수의 근
- 복소수의 그래픽 표현