단항식을 사용한 연산

9월 17, 2023

이 페이지에서는 단항식(덧셈, 뺄셈, 곱셈, 나눗셈, 거듭제곱)을 사용하여 모든 연산을 수행하는 방법을 설명합니다. 또한 각 연산 유형의 예를 단항식으로 살펴보고, 단계별로 풀어보는 연습문제를 통해 연습할 수 있습니다.

단항식의 덧셈과 뺄셈

두 개 이상의 단항식은 유사한 단항식인 경우, 즉 두 단항식의 문자 부분이 동일한 경우(동일한 문자 및 동일한 지수)에만 더하거나 뺄 수 있습니다.

그러면 두 개의 유사한 단항식의 합(또는 빼기)은 동일한 리터럴 부분과 이 두 단항식 계수의 합(또는 빼기)으로 구성된 다른 단항식과 같습니다.

단항식의 덧셈과 뺄셈은 각각 단항식의 덧셈과 뺄셈이라고도 합니다.

단항식의 덧셈과 뺄셈의 예

두 개 이상의 단항식을 더하고 빼는 방법을 명확하게 이해할 수 있도록 아래에 몇 가지 예를 남겨드립니다.

$4x^6+3x^6 = 7x^6$
$5y^3-2y^3 = 3y^3$
$2x^2y+5x^2y-3x^2y = 4x^2y$
$6abc-7abc+4abc = 3abc$
$6x^3y^2-4x^3y+2x^2y^3 = \color{red} \bm{\times}$

마지막 예의 단항식은 유사하지 않거나, 즉 미지수나 지수가 다르기 때문에 더하거나 뺄 수 없습니다.

단항식의 곱의 곱

단항식의 곱을 숫자로 풀려면 단항식의 계수에 해당 숫자를 곱하고 단항식의 문자 부분은 그대로 두십시오.

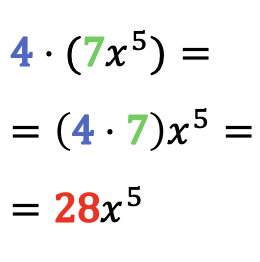
숫자에 단항식을 곱하는 예

$2\cdot (6x^3) = (2\cdot 6)x^3 = 12x^3$
$-4\cdot (5x^7) = (-4\cdot 5)x^7 = -20x^7$
$5\cdot (-3a^4b) = (5\cdot (-3))a^4b = -15a^4b$
$-7(-6x^9y^5)= (-7\cdot (-6))x^9y^5=42x^9y^5$

단항식의 곱셈

두 단항식의 곱셈 의 결과는 계수가 단항식의 계수의 곱이고 리터럴 부분이 동일한 밑을 갖는 변수를 곱함으로써, 즉 지수를 더함으로써 얻어지는 또 다른 단항식입니다.

따라서 두 개의 서로 다른 단항식을 곱하려면 둘 사이의 계수를 곱하고 동일한 밑수를 갖는 거듭제곱의 지수를 더해야 합니다.

그러나 기본 거듭제곱이 다른 두 개의 단항식을 곱하는 경우 계수를 함께 곱하고 거듭제곱을 동일하게 유지하기만 하면 됩니다. 예를 들어:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

반면, 단항식을 곱할 때는 부호의 법칙을 고려해야 합니다.

양의 단항식에 양의 단항식을 곱하면 또 다른 양의 단항식이 생성됩니다.
양의 단항식에 음의 단항식을 곱하면(또는 그 반대) 음의 단항식과 같습니다.
두 개의 음의 단항식을 곱하면 양의 단항식이 생성됩니다.

단항식 곱셈의 예

다음은 단항식 간의 곱셈에 대한 몇 가지 예이므로 어떻게 수행되는지 확인할 수 있습니다.

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

보시다시피, 단항식의 곱셈을 푸는 것은 비교적 간단합니다. 하지만 단항식에 다항식을 곱할 수도 있고, 2개 이상의 다항식도 함께 곱할 수 있다는 점을 명심해야 합니다. 더 관심이 있으시면 다항식 곱셈을 클릭하여 이러한 모든 연산이 어떻게 작동하는지 확인할 수 있습니다.

단항식의 나눗셈

수학에서, 단항식 나눗셈 의 결과는 계수가 단항식 계수의 몫과 동일하고 문자 그대로의 부분이 동일한 밑수를 갖는 변수를 나누어, 즉 지수를 빼서 얻어지는 또 다른 단항식입니다. .

분명히, 단항식의 나눗셈은 분수로도 표현할 수 있습니다:

$8x^3y^2z : 2x^2y = \cfrac{8x^3y^2z}{2x^2y} = 4xyz$

곱셈에서와 마찬가지로 단항식의 나눗셈에서도 부호의 법칙을 적용해야 합니다.

양의 단항식을 양의 단항식으로 나눈 값은 또 다른 양의 단항식을 제공합니다.
양의 단항식을 음의 단항식으로 나눈 값(또는 그 반대)은 음의 단항식과 동일합니다.
두 개의 음의 단항식이 서로 나누어지면 양의 단항식이 생성됩니다.

단항식의 나눗셈의 예

아래에서 두 개 이상의 단항식을 나누는 방법에 대한 더 많은 예를 볼 수 있습니다.

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

분명히 어느 시점에서 수학에서 새로운 것을 배웠을 때 스스로에게 질문했습니다. 그것은 무엇을 위한 것인가 ? 음, 단항식 나눗셈은 다항식을 나누는 데 사용됩니다. 실제로 두 개의 단항식이 잘못 나누어졌기 때문에 다항식을 나누는 실수를 저지르는 것이 매우 일반적입니다. 이것이 바로 여러분이 단항식 사이의 나눗셈에 익숙해졌으니 이제 다항식의 나눗셈이 어떻게 계산되는지 볼 것을 권장하는 이유입니다. 이제 절차를 배우는 것이 훨씬 쉬울 것이기 때문입니다(상당히 복잡합니다).

단항식의 거듭제곱

수학에서는 단항식의 거듭제곱을 계산하기 위해 단항식의 각 요소를 거듭제곱의 지수로 올립니다 . 즉, 단항식의 거듭제곱은 계수와 변수(문자)를 거듭제곱의 지수로 높이는 것으로 구성됩니다.

둘 다 이미 높은 항을 올릴 때 지수가 곱해진다는 거듭제곱의 속성을 기억하세요. 이것이 단항식의 거듭제곱에 따라 각 문자의 지수에 거듭제곱을 나타내는 지수가 항상 곱해지는 이유입니다.

반면, 이 작업을 올바르게 수행하려면 다음과 같은 권한 속성을 기억해야 합니다.

짝수 지수로 거듭제곱된 음의 단항식은 양의 단항식과 동일합니다.
대신, 홀수 지수로 거듭제곱된 음의 단항식은 음의 단항식이 됩니다.

단항식의 거듭제곱의 예

단항식의 거듭제곱이 어떻게 계산되는지 명확하게 이해할 수 있도록 몇 가지 예를 제시합니다.

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

단항식과 결합된 연산

단항식을 사용하는 모든 연산이 무엇인지 확인한 후에는 서로 결합할 수도 있다는 것을 알아두십시오. 즉, 우리는 덧셈, 뺄셈, 곱셈, 나눗셈, 거듭제곱 등 모든 유형이 관련된 단항식을 사용하여 연산을 해결하도록 요청받는 연습을 찾을 수 있습니다.

하지만 걱정하지 마세요. 보이는 것만큼 어렵지는 않습니다. 기억해야 할 유일한 것은 결합된 작업이 해결되는 순서입니다.

먼저, 괄호 안의 단항식을 사용한 연산이 해결됩니다.
그런 다음 단항식의 거듭제곱이 계산됩니다.
셋째, 단항식의 곱셈과 나눗셈을 수행한다.
그리고 마지막으로 단항식의 덧셈과 뺄셈이 결정됩니다.

예제를 풀면 더 명확하게 알 수 있을 것이라고 확신합니다.

단항식의 결합 연산 예

$12x^9:(2x^4-8x^4)+3x^4\cdot 6x - (x^3\cdot 7x^2)$

우선, 괄호 안의 단항식을 사용하여 연산을 풀어야 합니다.

$12x^9:(-6x^4)+3x^4\cdot 6x - 7x^5$

이 경우 우리에게는 힘이 없습니다. 이제 단항식의 곱셈과 나눗셈을 계산해 보겠습니다.

$-2x^5+18x^5 - 7x^5$

그리고 마지막으로 단항식을 더하고 뺍니다.

$16x^5 - 7x^5$

$\bm{9x^5}$

단항식 연산에 대한 연습 문제 해결

연습하고 싶다면 단항식 연산에 대한 ESO 난이도를 단계별로 해결하는 몇 가지 연습을 아래에 남겨두겠습니다.

연습 1

다음과 같은 단항식의 덧셈과 뺄셈을 계산합니다.

$\text{A)} \ 2x^4+9x^4$

$\text{B)} \ -3x^5y^3 +4x^5y^3$

$\text{C)} \ 3x^8-6x^8+2x^8$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2$

$\text{E)} \ 6xyz-5xz-7xyz-8xz$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3$

솔루션 보기

$\text{A)} \ 2x^4+9x^4= \bm{11x^4}$

$\text{B)} \ -3x^5y^3 +4x^5y^3= \bm{x^5y^3}$

$\text{C)} \ 3x^8-6x^8+2x^8= \bm{-x^8}$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2=\bm{-7a^3b^2}$

$\text{E)} \ 6xyz-5xz-7xyz-8xz= \bm{-xyz-13xz}$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3 = \bm{-2y^5+8y^4+3y^3}$

연습 2

다음 단항식의 곱셈을 푼다:

$\text{A)} \ 5x^7\cdot 6x^2$

$\text{B)} \ 2y^8\cdot (-5y^6)$

$\text{C)} \ -4a^3 \cdot (-2a)$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6)$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)$

솔루션 보기

$\text{A)} \ 5x^7\cdot 6x^2=(5\cdot 6)x^{7+2} = \bm{30x^9}$

$\text{B)} \ 2y^8\cdot (-5y^6)= (2\cdot (-5))y^{8+6} = \bm{-10y^{14}}$

$\text{C)} \ -4a^3 \cdot (-2a) =(-4\cdot (-2))a^{3+1} = \bm{8a^4}$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6) = 8x^4\cdot (-3x^6) = \bm{-24x^{10}}$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)=5x^9\cdot (-9x^4) =\bm{-45x^{13}}$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-bb20ebb96e0dff759d07813f6fff9470_l3.png" height="22" width="195" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[35x^{11}y^2z^4\cdot (-2x^2y^5z^3) =\]" title="Rendered by QuickLaTeX.com"/> \bm{-70x^{13}y^7z^7}” title=”Rendered by QuickLaTeX.com”> <div class=$

연습 3

다음 단항식 나눗셈의 결과를 결정합니다.

$\text{A)} \ 24x^4: 6x^2$

$\text{B)} \ 16a^9: (-2a^6)$

$\text{C)} \ -21x^3:(-3x)$

$\text{D)} \ 14x^8y^3 :2x^6y$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)$

솔루션 보기

$\text{A)} \ 24x^4: 6x^2 = (24:6)x^{4-2} = \bm{4x^2}$

$\text{B)} \ 16a^9: (-2a^6)= (16:(-2))a^{9-6} = \bm{-8a^3}$

$\text{C)} \ -21x^3:(-3x) = (-21:(-3))x^{3-1} = \bm{7x^2}$

$\text{D)} \ 14x^8y^3 :2x^6y = \bm{7x^2y^2}$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4= 6x^3y^0z^2=\bm{6x^3z^2}$

이전 작업에서는 용어를 단순화했습니다.

$y^0$

0으로 올림된 모든 숫자는 1과 같기 때문입니다. 따라서:

$6x^3y^0z^2=6x^3\cdot 1 \cdot z^2=\bm{6x^3z^2}$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-6dc0e068dbf84cef6abfe7e1789d245b_l3.png" height="22" width="194" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[-8x^4y^4z^6: (-4x^2y^2z^3)=\]" title="Rendered by QuickLaTeX.com"/> \bm{2x^2y^2z^3}” title=”Rendered by QuickLaTeX.com”> <div class=$

연습 4

다음과 같은 단항식의 거듭제곱을 구하세요.

$\text{A)} \ \left(-8x^4\right)^2$

$\text{B)} \ \left(-2a^7\right)^3$

$\text{C)} \ \left(5x^8y^2\right)^3$

$\text{D)} \ \left(-x^3y^5z\right)^6$

$\text{E)} \ \left(-2x^5y^4\right)^5$

솔루션 보기

$\text{A)} \ \left(-8x^4\right)^2=(-8)^2\left(x^4\right)^2 = (-8)^2x^{4\cdot 2} = \bm{64x^{8}}$

$\text{B)} \ \left(-2a^7\right)^3=(-2)^3\left(a^7\right)^3 = (-2)^3a^{7\cdot 3} = \bm{-8a^{21}}$

$\text{C)} \ \left(5x^8y^2\right)^3=(5)^3\left(x^8y^2\right)^3 = \bm{125x^{24}y^6}$

$\text{D)} \ \left(-x^3y^5z\right)^6=(-1)^6\left(x^3y^5z\right)^6 = \bm{x^{18}y^{30}z^{6}}$

$\text{E)} \ \left(-2x^5y^4\right)^5 =(-2)^5\left(x^5y^4\right)^5 = \bm{-32x^{25}y^{20}}$

연습 5

단항식과 결합된 다음 연산을 풀고 최대한 단순화하십시오.

$\text{A)} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$\text{B)} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$\text{C)} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$\text{D)} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$\text{E)} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

솔루션 보기

$\color{blue} \mathbf{A}\bm{)} \color{black} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$12x^7 : 2x^4 -5x^2\cdot 6x$

$6x^3 -30x^3$

$\bm{-24x^3}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$4\cdot \left(3x^4 \right)^2$

$4\cdot 9x^8$

$\bm{36x^8}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$8x^7:(-8x^3)-5x^3\cdot 3x$

$-x^4-15x^4$

$\bm{-16x^4}$

$\color{blue} \mathbf{D}\bm{)} \color{black} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5\cdot x^4y^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5x^4y^4:(-2y)$

$-8x^6y^3+20x^6y^4:(-2y)$

$-8x^6y^3-10x^6y^3$

$\bm{-18x^6y^3}$

$\color{blue} \mathbf{E}\bm{)} \color{black} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

$8x^8:\left(-2x^3\right)^2-42x^9: (-2x^4)$

$8x^8:4x^6-42x^9: (-2x^4)$

$\bm{2x^2+21x^5}$

두 단항식의 지수가 다르기 때문에 연산을 더 이상 단순화할 수 없으며 결과는 다항식이 됩니다.

여기까지 왔다면 이미 단항식의 모든 연산을 마스터했다는 의미입니다. 밝은! 글쎄, 당신이 확실히 관심을 가질 또 다른 연산은 숫자의 계승입니다. 이것은 다른 연산과 다르게 계산되기 때문에 다소 흥미로운 연산입니다. 그리고 사실, 많은 사람들은 숫자의 계승이 무엇인지 모릅니다. 이 링크를 클릭하여 계승 문제를 해결하는 방법을 알아보세요.

단항식의 덧셈과 뺄셈

단항식의 덧셈과 뺄셈의 예

단항식의 곱의 곱

숫자에 단항식을 곱하는 예

단항식의 곱셈

단항식 곱셈의 예

단항식의 나눗셈

단항식의 나눗셈의 예

단항식의 거듭제곱

단항식의 거듭제곱의 예

단항식과 결합된 연산

단항식의 결합 연산 예

단항식 연산에 대한 연습 문제 해결

연습 1

연습 2

연습 3

연습 4

연습 5

댓글 달기 댓글 취소