Magic Squares는 재미있고 흥미로운 방식으로 계산 능력을 훈련시키는 수학 퍼즐 게임입니다. 이것이 바로 어린 학생들에게 수학을 가르치는 최고의 자료 중 하나인 이유입니다.
매직 어레이란 무엇이며 어떻게 해결됩니까?
마방진은 정수가 쓰여진 다양한 상자로 구성된 일종의 테이블 또는 행렬입니다. 그러나 어떠한 경우에도 설치할 수 없습니다. 일련의 규칙을 준수해야 합니다.
- 모든 마법합(가로, 세로 또는 대각선의 모든 값의 합)은 항상 마법 상수와 동일한 값을 제공해야 합니다(단일 값입니다).
- 어떤 숫자도 두 번 반복될 수 없습니다.
- 연속된 숫자(예: 1부터 9까지) 또는 특정 계열을 따르는 숫자(예: 홀수, 5의 배수 등)만 사용할 수 있습니다.
또한 구조에 따라 정사각형을 다르게 분류할 수 있다는 점을 강조하는 것이 중요합니다. 첫 번째는 행이나 열에 있는 셀의 수와 동일한 사각형의 각도 에 따른 것입니다. 그리고 두 번째는 테이블의 정도 유형( 짝수 또는 홀수)에 따른 것입니다. 이러한 구별을 통해 모든 사각형을 서로 다른 범주로 구성할 수 있습니다. 이에 대해서는 나중에 자세히 설명하겠습니다.
마방진을 해결하는 방법은 무엇입니까?
이 수학 게임을 풀기 위해 우리는 기하학을 사용하거나 마법 상수를 계산하는 두 가지 방법을 사용할 수 있습니다. 두 절차 모두 동일하게 유효하지만 한 절차는 결과를 더 빨리 얻을 수 있는 반면 다른 절차는 더 많은 시간과 추론이 필요합니다. 다음으로 두 가지 방법을 모두 설명하므로 원하는 방법을 선택하여 각 상황에 더 잘 적응할 수 있습니다.
마방진의 공식은 무엇입니까?
첫 번째 방법은 마법 상수를 계산하는 것으로 구성되며, 이에 대해 다음 공식을 사용해야 합니다: n(n 2 +1)/2, 여기서 n은 제곱의 각도입니다. 그리고 이 값을 얻은 후에 남은 것은 다양한 숫자 조합을 시도하는 것뿐입니다. 이를 통해 전체 사각형의 마법 합을 상수와 동일하게 만들 수 있습니다. 즉, 전체 그림이 균형을 이루도록 상수의 값을 합산하는 숫자의 조합을 형성해야 합니다.
기하학을 사용하여 마방진을 해결하는 방법은 무엇입니까?
둘째, 기하학을 사용하여 마방진을 풀 수 있습니다. 이 방법은 매우 간단하고 순전히 체계적이므로 계산 기술을 연습할 필요가 없다는 점에 유의해야 합니다. 즉, 짝수 제곱과 홀수 제곱을 모두 푸는 절차를 설명하겠습니다.
홀수로 된 마방진을 어떻게 푸나요?
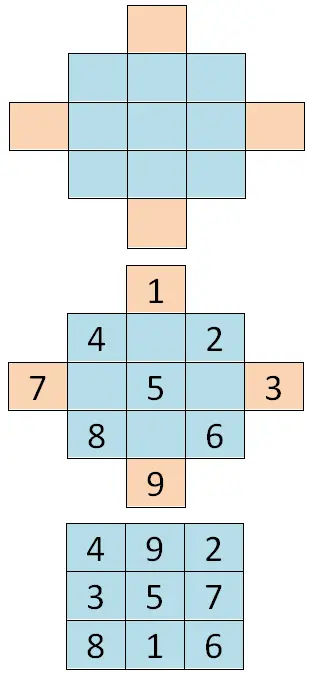
이 첫 번째 사례를 해결하려면 일종의 다이아몬드를 갖도록 초기 테이블에 셀을 추가해야 합니다. 그런 다음 시리즈의 첫 번째 숫자(이 경우 1)부터 시작하여 모든 연속 숫자를 작성해야 하며 다이아몬드의 대각선을 따라갑니다. 마지막으로 숫자를 “두 배로” 늘려야 하므로 외부 셀의 값이 반대쪽으로 이동합니다. 따라서 수직 축의 외부 셀이 교차하고 수평 축의 셀에서도 동일한 일이 발생합니다. 아래에서 예를 볼 수 있습니다.
짝수 마방진을 해결하는 방법은 무엇입니까?
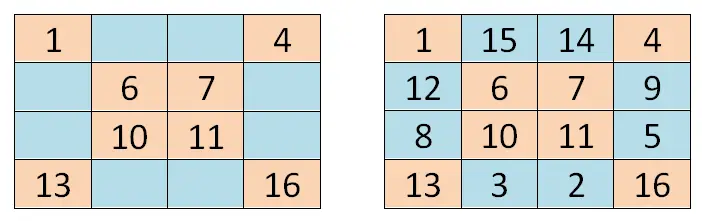
짝수 마방진(행 과 열의 수가 짝수인 마방진)을 풀기 위해 이전 방법과 다소 다르지만 역시 기하학을 기반으로 하는 방법을 사용할 수 있습니다. 왼쪽 상단에 시리즈의 첫 번째 숫자(이 경우 1)를 쓰는 것부터 시작하겠습니다. 그런 다음 두 개의 주 대각선을 탐색하고 각 상자의 위치에 해당하는 값을 작성합니다.
두 개의 주 대각선을 작성한 후에는 오른쪽 하단 모서리부터 시작하는 첫 번째 빈 상자(이 경우 상자 15)에 배치해야 합니다. 거기에서 계열의 두 번째 값을 쓰고 나머지 값을 순서대로(가장 작은 것부터 큰 것까지) 써서 오른쪽에서 왼쪽으로 , 아래에서 위로 셀을 완성합니다. 더 명확하게 하기 위해 아래에 표시된 이미지를 통해 방향을 잡을 수 있습니다.
마방진을 만드는 방법은 무엇입니까?
마방진을 직접 만들려면 몇 가지 절차를 따를 수 있으며 그중 두 가지를 강조하겠습니다. 각 방법은 서로 다른 유형의 사각형을 만드는 데 사용되므로 생성하려는 사각형에 따라 방법을 신중하게 선택해야 합니다.
샴 방식
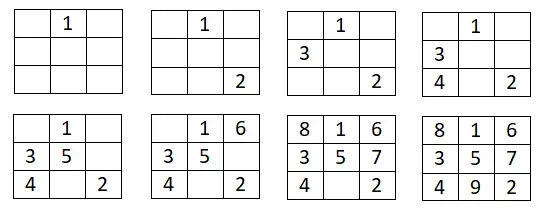
이 첫 번째 방법은 매우 간단하며 특히 어떤 크기의 이상한 마방진을 만드는 데 도움이 됩니다. 따라야 할 절차는 매우 간단합니다. 기본적으로 첫 번째 행의 중앙 상자에 시리즈의 첫 번째 숫자를 씁니다. 거기에서 우리가 선택한 산술 진행 순서대로 돌아가서 다음 숫자를 위쪽과 오른쪽에 씁니다. 하지만 이 위치가 그려진 사각형 외부에 있으면 마지막 행이나 열로 이동해야 합니다. 그리고 우리가 완전한 정사각형으로 끝나면 우리가 입력한 마지막 숫자 정사각형에서 한 정사각형 아래로 내려간 다음 동일한 방식으로 계속할 것입니다.
아래에서 3×3의 예를 볼 수 있습니다.
마방진에 대한 Strachey의 방법
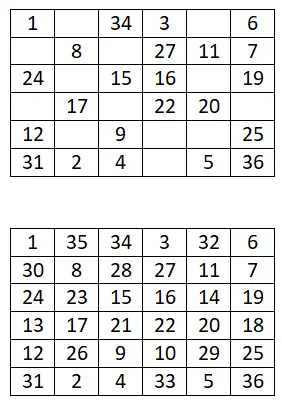
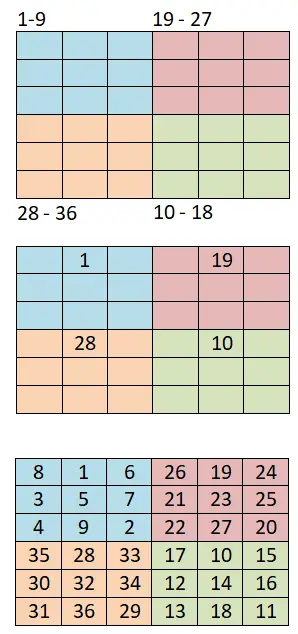
4k + 2 쌍의 마방진을 생성하기 위해 이전 방법(샴 방법)을 기반으로 하고 역시 매우 간단한 다른 방법을 사용합니다. 아래에서 따라야 할 단계와 6×6 마방진의 작업 예를 볼 수 있습니다.
- 더 작은 사분면으로 나누기: 가장 먼저 해야 할 일은 보드를 더 작은 정사각형으로 나누는 것입니다. 예를 들어 6×6 보드가 있는 경우 3×3 정사각형의 동일한 사분면 4개를 만들어야 합니다.
- 샴 방법을 사용합니다. 그런 다음 각 작은 사분면에 숫자 범위를 할당합니다. 예를 들어 1로 시퀀스를 시작하면 범위는 1-9(첫 번째), 10-18(4번째), 19-27이 됩니다. (두 번째) 및 28-36(세 번째).
Conway의 마방진에 대한 LUX 방법
우리는 4n + 2 차의 마방진을 생성하고자 할 때 후자의 시스템을 사용할 것입니다. 여기서 n은 자연수입니다. 따라서 이 스타일의 사각형을 만들기 위해 따라야 할 절차는 다음과 같습니다.
- 테이블 또는 행렬 생성: 2n + 1차 행렬을 생성하는 것부터 시작합니다. 여기서 n은 자연수입니다. 이를 통해 우리는 테이블을 디자인할 수 있고 그 정도를 염두에 두고 디자인을 시작하게 됩니다.
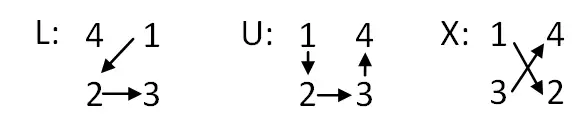
- 문자 위치 지정: 테이블이 구성되면 위에서 아래로 L의 n + 1줄, U의 1줄, X의 n – 1줄을 써야 합니다. 그런 다음 U를 바꿔야 합니다. 중간에 L이 맨 위에 있습니다.
- 숫자 값에 대한 문자 바꾸기: 이제 문자를 4개의 연속 숫자 그룹으로 바꿔야 합니다. 편지에 따라 우리는 숫자에 하나 또는 다른 명령을 내릴 것입니다. 아래에 설명되어 있습니다:
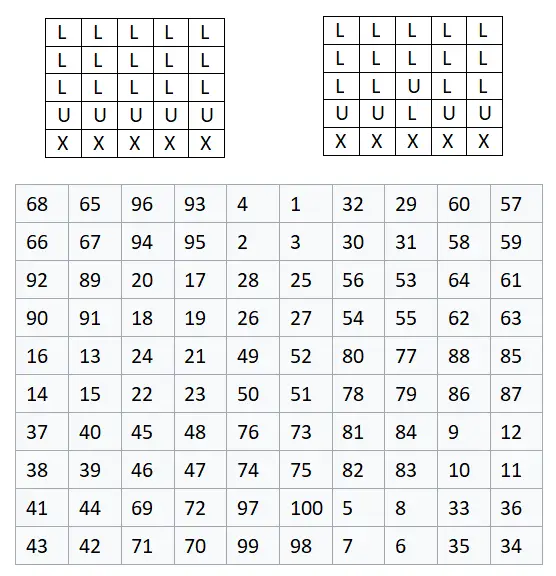
5×5 행렬을 구성하는 것부터 시작하겠습니다. 따라서 n = 2입니다. 왜냐하면 2n + 1 = 2 · 2 + 1 = 5이기 때문입니다. 이는 행렬의 크기가 10×10이 된다는 것을 의미합니다. 우리는 이미 문자를 포함하는 각 셀이 4개의 숫자 그룹, 즉 2×2 행렬과 동일하다고 말했습니다. 아래에서는 각 문자를 이미지에 표시된 순서대로 4개의 숫자 그룹으로 대체한 완성된 예를 볼 수 있습니다.
마방진 운동
다음으로, 우리는 불완전한 마방진을 제공하며 이 글에서 설명한 개념 덕분에 스스로 채워야 합니다. 배운 방법 중 무엇이든 사용할 수 있다는 것을 기억하십시오. 또한 1이 선언에 포함되더라도 시리즈의 첫 번째 숫자가 아닐 수도 있다는 점을 고려해야 합니다. 그리고 연습 중 하나를 마치면 문장 아래에서 해결 방법을 볼 수 있습니다.
3×3 마방진
홀수로만 3×3 마방진을 만드세요:
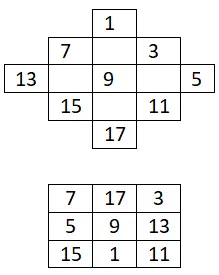
4×4 마방진
다음 4×4 마방진을 완성하세요:
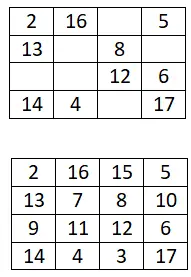
5×5 마방진
다음 5×5 마방진을 완성하세요:
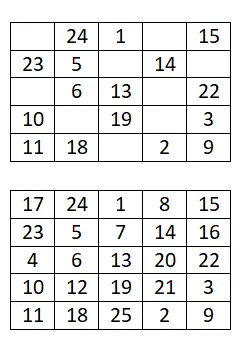
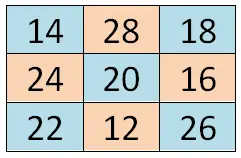
6×6 마방진
다음 6×6 마방진을 완성하세요: