아크코사인의 미분

여기에서는 함수의 아크코사인을 유도하는 방법을 설명합니다. 또한, 아크코사인의 미분 예를 찾아볼 수 있으며, 단계별로 풀어보는 연습문제를 통해 연습할 수 있습니다. 마지막으로 아크코사인 미분 공식의 증명을 보여드리겠습니다.

아크 코사인의 미분은 무엇입니까?

x의 아크코사인 미분은 1에서 x 제곱을 뺀 제곱근에 대한 음의 1입니다.

$f(x)=\text{arccos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{\sqrt{1-x^2}}$

따라서 함수의 아크코사인 도함수는 해당 함수의 도함수를 1에서 해당 함수의 제곱을 뺀 제곱근으로 나눈 몫과 같습니다.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

실제로 첫 번째 공식은 두 번째 공식의 x를 u로 대체하여 얻습니다. 요약하면 역코사인의 미분 공식은 다음과 같습니다.

보시다시피, 아크코사인 도함수 공식은 아크사인 도함수와 비슷하지만 앞에 음수를 추가합니다.

아크코사인 파생물의 예

아크코사인 함수의 도함수에 대한 공식이 주어지면 이제 이러한 유형의 삼각함수 도함수에 대한 몇 가지 예를 분석하겠습니다. 이렇게 하면 함수의 아크코사인이 어떻게 파생되는지 이해하는 것이 더 쉬울 것입니다.

예시 1: 2x 아크코사인의 파생

$f(x)=\text{arccos}(2x)$

아크 코사인의 미분을 풀기 위해 다음 공식을 사용합니다.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

2x의 도함수는 2이므로 2x의 아크 코사인 도함수는 루트 1에서 2x 제곱을 뺀 값에 대해 -2입니다.

$f(x)=\text{arccos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\sqrt{1-(2x)^2}}=-\cfrac{2}{\sqrt{1-4x^2}}$

예 2: x 제곱의 아크코사인 파생

$f(x)=\text{arccos}(x^2)$

우리는 도함수를 계산하기 위해 체인 규칙과 함께 아크코사인 도함수 공식을 적용합니다:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

함수 x ² 의 미분은 2x이므로 x의 아크코사인을 2제곱으로 미분하면 다음과 같습니다.

$f(x)=\text{arccos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=-\cfrac{2x}{\sqrt{1-x^4}}$

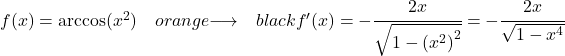
예제 3: 로그의 아크코사인 파생

$f(x)=\text{arccos}\bigl(\ln (x)\bigr)$

이 예의 함수는 아크코사인과 자연로그로 구성된 함수이므로 이를 도출하려면 연쇄법칙을 사용해야 합니다.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

자연 로그의 도함수는 1을 x로 나눈 값이므로 정수 함수의 도함수는 다음과 같습니다.

$f(x)=\text{arccos}\bigl(\ln (x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\cfrac{1}{x}}{\sqrt{1-\left(\ln(x)\right)^2}}=\cfrac{1}{x\sqrt{1-\ln^2(x)}}$

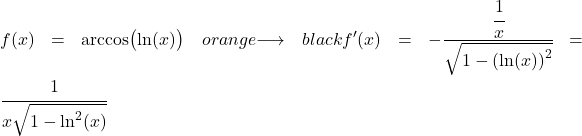
Arccosine 파생물이 문제를 해결했습니다.

다음 아크코사인 함수를 도출합니다.

$\text{A) }f(x)=\text{arccos}(7x)$

$\text{B) }f(x)=\text{arccos}(x^3+6x)$

$\text{C) }f(x)=\text{arccos}^3\left(e^{3x}\right)$

$\text{D) }f(x)=\text{arccos}\left(\log_3(x^3)\right)$

$\text{E) }f(x)=\text{arccos}\left(\sqrt{4x}\right)$

해결책 보기

$\text{A) }f'(x)=-\cfrac{7}{\sqrt{1-(7x)^2}}=-\cfrac{7}{\sqrt{1-49x^2}}$

$\text{B) }f'(x)=-\cfrac{3x^2+6}{\sqrt{1-(x^3+6x)^2}}$

$\begin{aligned}\text{C) }\displaystyle f'(x)&=3\text{arccos}^2\left(e^{3x}\right)\cdot \left(-\frac{3e^{3x}}{\sqrt{1-\left(e^{3x}\right)^2}}\right)\\[1.5ex] &=-\cfrac{9\text{arccos}^2\left(e^{3x}\right)\cdot e^{3x}}{\sqrt{1-e^{6x}}}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)&=-\cfrac{1}{\sqrt{1-\left(\log_3(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 3}\\[1.5ex] &=-\cfrac{1}{x\cdot \ln 3\cdot \sqrt{1-\log_3^2(3x)}} \end{aligned}$

$\begin{aligned}\text{E) } f'(x)& =-\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=-\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=-\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$