오일러 상수 (오일러 상수라고도 함)는 정수론, 위상수학, 군론, 함수론 등 수학의 다양한 분야에서 중요하고 필수적인 수학 수입니다. 그리스 문자 “e”로 표시되며 대략적인 값은 2.71828입니다.
숫자 e는 지수 함수의 공식을 따르며 복소수 이론의 기본 숫자입니다.
확률을 계산하고 성장과 붕괴 과정을 모델링하는 등 많은 수학적 문제를 풀 때 나타나는 자연수이기도 합니다.
오일러 수의 유래는 무엇입니까?
오일러 수는 역사상 가장 위대한 수학자 중 한 명이자 현대 수학의 아버지로 여겨지는 스위스 수학자 레온하르트 오일러( Leonhard Euler , 1707-1783)의 이름을 따서 명명되었습니다.
오일러는 정수론, 기하학, 미적분학, 물리학, 천문학 등 수학의 여러 분야에 귀중한 공헌을 했습니다.
로그 계산 및 이론에 대한 연구에서 숫자 e (오일러 수라고 함)를 처음으로 정의하고 사용한 사람이 바로 그 사람이었습니다. 복소수에 대한 오일러의 공식은 수학에 대한 그의 가장 주목할만한 공헌 중 하나이기도 합니다.
이 값은 어떻게 얻어지나요?
실제로 오일러 수를 계산하는 방법에는 여러 가지가 있습니다. 그러나 두 방법 모두 정확한 결과를 제공하지 않는다는 점은 언급할 가치가 있습니다. 따라서 번호 매기기는 연속적이고 무한하지만 반복되지는 않습니다.
실제로 현재 숫자 e를 구성하는 숫자는 1조 개가 넘는 것으로 알려져 있습니다. 오일러 수를 정의하는 무한 급수는 다음과 같습니다.

금 “!” 팩토리얼은 해당 숫자까지의 모든 자연수의 곱으로 정의됩니다. 예를 들어:
5! = 5 4 3 2 1 = 120
이 계열은 높이가 1이고 너비가 감소하는 일련의 직사각형 의 합으로 그래픽으로 볼 수 있습니다. 여기서 각 직사각형의 너비는 1/n!입니다. 여기서 n은 계승의 수입니다.
합에서 직사각형의 수를 늘리면 지수 함수 곡선 아래 면적의 근사치는 오일러 수에 점점 더 가까워집니다.
요약하자면, 오일러 수는 무한 급수의 합으로 생성되는 수이며 수학의 여러 영역에서 기본이 됩니다. 무리수 이지만 대략적인 값 은 2.71828입니다.
오일러 자신이 e를 소수점 18자리까지 계산하기 위해 이 방법을 구현했다는 점을 명심하는 것이 중요합니다.
그것을 계산하는 또 다른 방법:
일련 의 유한항을 사용하여 직선의 오일러 수의 대략적인 값을 계산할 수 있습니다. 예를 들어 위에서 정의한 첫 번째 무한 계열을 사용하면 다음과 같습니다.

계열의 첫 번째 항을 추가하여 대략적인 값을 계산할 수 있습니다. 예를 들어 처음 6개의 항을 추가하면 다음과 같습니다.
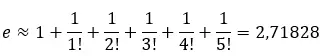
이 계열을 선으로 그려 대략적인 값인 2.71828에 어떻게 접근하는지 확인할 수 있습니다.
그래픽적으로, 오일러 수를 나타내는 선은 높이가 1이고 폭이 감소하는 일련의 직사각형으로 그릴 수 있습니다. 여기서 각 직사각형의 폭은 1/n!입니다. 여기서 n은 계승의 수입니다.
합에서 직사각형의 수를 늘리면 지수 함수 곡선 아래 면적의 근사치는 오일러 수에 점점 더 가까워집니다.
오일러 수를 사용한 지수 방정식
오일러 수를 사용한 지수 방정식은 물리학, 생물학, 경제학 등 과학의 다양한 현상을 모델링하는 데 사용할 수 있습니다. 여기 몇 가지 예가 있어요.
기하급수적인 성장과 쇠퇴
이 모델은 인구가 증가하거나 감소하는 속도 또는 독성 물질이 분해되는 속도를 설명합니다.
예를 들어, 인구가 연간 5%씩 증가한다면 그 규모는 다음 공식으로 설명할 수 있습니다.
P(t) = P0 · e 0.05t , 여기서 P0은 초기 모집단 크기입니다.
방사성 붕괴 모델
이 모델은 시간이 지남에 따라 방사성 원자가 붕괴되는 속도를 설명합니다.
공식은 다음과 같습니다.
N(t) = N0 e – λt
여기서 N0는 초기 원자 수, λ는 방사성 물질에 따라 달라지는 상수, t는 시간입니다.
이는 오일러 수를 사용한 지수 방정식이 실제로 어떻게 사용될 수 있는지에 대한 몇 가지 예일 뿐입니다. 지수 방정식이 유용하고 관련성이 있는 다른 영역도 많이 있습니다.
오일러 수의 응용은 무엇입니까?
오일러 수는 수학과 과학의 다양한 분야에서 폭넓게 응용됩니다. 숫자 e가 사용되는 일부 필드는 다음과 같습니다.
- 계산 및 수학적 분석 : 지수 및 로그 함수 연구와 미분 방정식의 해결에 사용됩니다.
- 정수론 – 소수의 분포를 연구하고 정수론과 관련된 문제를 해결하는 데 사용됩니다.
- 확률 및 통계 : 확률 분포와 관련된 문제를 해결하고 기대값을 추정하는 데 사용됩니다.
- 암호화 – 암호화 및 암호 해독 알고리즘 연구에 사용됩니다.
- 물리학 – 열역학, 양자 역학 및 통계 물리학과 관련된 문제를 해결하는 데 사용됩니다.
- 화학 : 화학적 열역학 및 화학적 동역학과 관련된 문제를 해결하는 데 사용됩니다.
복소수에 대한 오일러의 공식
복소수 에 대한 오일러의 공식은 삼각함수와 지수함수 사이의 관계를 설정합니다. 공식은 다음과 같이 작성됩니다.

여기서 “e”는 자연 로그의 밑이고, “i”는 허수 단위, “x”는 실수, “cos”와 “sin”은 각각 삼각 함수 코사인과 사인입니다.
이 공식은 정수론, 함수론, 복잡도 이론 등 수학의 여러 분야에서 매우 유용하며 공학, 물리학, 경제학 등 다양한 분야에 응용됩니다.
이를 사용하는 실제적인 예는 푸리에 분석에서 신호 및 시스템을 표현하는 데 있으며, 여기서 주기적 신호는 복잡한 정현파 신호의 합으로 표시됩니다.
오일러의 공식은 이러한 복잡한 신호가 개별 정현파 신호를 설명하는 실제 삼각 함수와 어떻게 관련되는지 설명하는 데 사용됩니다.
오일러 수와 복리
복리란 원금이라고 하는 일정 금액이 시간이 지남에 따라 증가하는 이자를 바탕으로 이자를 얻는 과정을 설명하는 금융 개념 입니다.
즉, 투자로 얻은 이자는 초기 자본뿐만 아니라 이전 기간에 얻은 이자에서도 발생합니다.
복리 계산 공식은 오일러 수를 사용하기 때문에 오일러 수와 복리 이자는 관련이 있습니다. 복리의 공식은 다음과 같습니다.
A = 퍼트
여기서 A는 최종 금액, P는 원금, r은 이자율, t는 시간, e는 오일러 수입니다. 이런 식으로 오일러 수는 복리 계산을 위한 수학적 공식에서 중요한 요소입니다.
구체적인 숫자로 복리를 계산하는 예는 다음과 같습니다.
2년 동안 연 5%의 이자율로 €1,000를 투자했다고 가정합니다. 복리를 계산하는 공식은 다음과 같습니다.
A = 퍼센트 = 1000 이자 0.05 2 = 1000 1.1025 = €1102.5.
이는 2년 후에 생성된 복리 이자로 인해 초기 자본금 €1,000가 €1,102.5로 증가한다는 것을 의미합니다.
오일러 수를 사용한 수학 연습의 예
다음은 오일러 수와 관련된 수학 문제를 해결한 두 가지 예입니다.
1. x가 실수인 “e ix “의 값을 찾습니다.
오일러의 항등식은 e ix = cos(x) + i · sin(x)임을 알려줍니다. 따라서 x의 값을 알면 삼각함수를 이용하여 eix 의 값을 계산할 수 있습니다.
2. 주어진 x 값에 대해 e^(x 2 )를 계산합니다.
Taylor 계열을 사용하여 e^(x 2 ) 값을 계산할 수 있습니다. e x 의 테일러 급수는 사용된 항에 따라 e x 값의 연속적인 근사치를 계산할 수 있게 해주는 무한 전개입니다.

이 급수에서 x를 x 2 로 대체하면 e^(x 2 )에 대한 Taylor 급수를 얻습니다.