두 점 사이의 거리 공식(기하학)

이 페이지에서는 기하학(공식)에서 두 점 사이의 거리를 계산하는 방법을 설명합니다. 또한 예를 볼 수 있을 뿐만 아니라 두 지점 사이의 거리 문제를 풀어서 연습할 수도 있습니다.

두 점 사이의 거리를 구하는 공식은 무엇입니까?

두 점 사이의 거리는 두 점을 연결하는 선분의 길이와 같습니다. 따라서 수학에서는 두 개의 서로 다른 점 사이의 거리를 결정하려면 해당 좌표 간의 차이의 제곱을 계산한 다음 해당 제곱의 합의 근을 찾아야 합니다.

즉, 데카르트 평면의 서로 다른 두 점 사이의 거리를 계산하는 데 사용되는 공식은 다음과 같습니다.

두 개의 서로 다른 점의 좌표를 고려하십시오.

$A(x_1,y_1) \qquad \qquad B(x_2,y_2)$

두 점 사이의 거리 공식은 다음과 같습니다.

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

이 공식은 벡터의 크기에서 나옵니다. 사실, 이 공식을 사용하여 우리가 하는 일은 실제로 문제의 두 점에 의해 결정되는 벡터의 크기를 계산하는 것입니다. 벡터의 모듈러스에 대한 설명에서 이에 대한 자세한 내용을 읽을 수 있습니다.

반면, 해석기하학에서는 피타고라스 정리를 사용하여 두 점 사이의 거리 공식을 증명할 수도 있습니다.

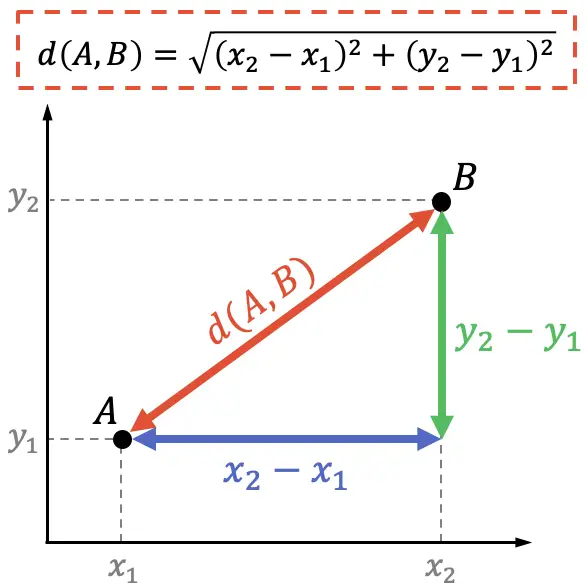
피타고라스 정리에 따르면 직각 삼각형의 빗변의 제곱은 다리의 제곱의 합과 같습니다. 따라서 다음과 같습니다.

$\bigl(d(A,B)\bigr)^2 = (x_2-x_1)^2 + (y_2-y_1)^2$

그리고 공식을 얻으려면 두 점 사이의 거리를 구하면 됩니다.

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

마지막으로, 3좌표 점으로 작업하는 경우 공간(R3)의 두 점 사이의 거리에 대한 공식은 동일하지만 Z 좌표를 추가한다는 점에 주목할 가치가 있습니다.

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2 \vphantom{\frac{1}{2}}}$

두 점 사이의 거리를 계산하는 예

두 점 사이의 거리에 대한 공식의 정의를 살펴보았으면 이제 예를 사용하여 해당 거리를 결정하는 방법을 살펴보겠습니다.

다음 두 점 사이의 거리를 구합니다.

$A(-1,7) \qquad \qquad B(3,4)$

두 점 사이의 거리를 기하학적으로 구하려면 다음 공식을 적용하면 됩니다.

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

이제 점의 좌표를 공식으로 대체합니다.

$d(A,B) = \sqrt{(3-(-1))^2+(4-7)^2 \vphantom{\frac{1}{2}}}$

그리고 우리는 계산을 합니다:

$\begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}$

따라서 두 점 사이의 거리는 5단위와 같습니다.

분명히 거리 값은 항상 양수 값을 제공해야 합니다. 거리는 항상 양수이기 때문입니다. 그렇지 않으면 단계에서 실수를 했다는 의미입니다.

두 지점 사이의 거리 문제 해결

연습 1

다음 두 점 사이의 거리를 계산합니다.

$A(4,2) \qquad \qquad B(1,5)$

해결책 보기

두 점 사이의 기하학적 거리를 찾으려면 다음 공식을 사용하면 됩니다.

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

이제 점의 좌표를 공식으로 대체합니다.

$d(A,B) = \sqrt{(1-4)^2+(5-2)^2 \vphantom{\frac{1}{2}}}$

그리고 우리는 계산을 합니다:

$\begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}$

연습 2

다음 두 점 사이의 거리를 구합니다.

$A(8,6) \qquad \qquad B(-4,1)$

해결책 보기

두 점 사이의 수학적 거리를 찾으려면 해당 공식을 사용해야 합니다.

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

이제 점의 좌표를 공식으로 대체합니다.

$d(A,B) = \sqrt{(-4-8)^2+(1-6)^2 \vphantom{\frac{1}{2}}}$

그리고 우리는 계산을 합니다:

$\begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}$

연습 3

아래 그래픽에 표시된 점 A, B, C로 형성된 삼각형의 둘레를 계산합니다.

해결책 보기

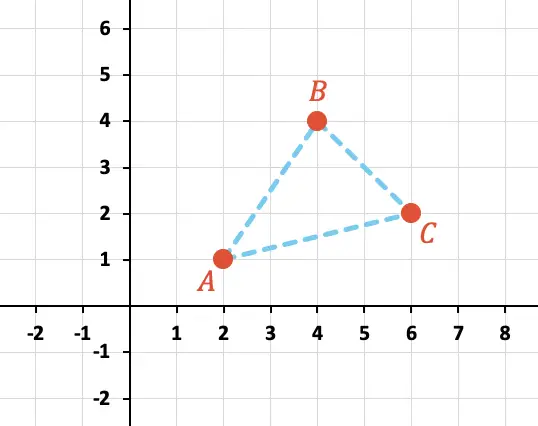
먼저 그래프에서 각 점의 X 및 Y 좌표를 식별해야 합니다.

$A(2,1)$

$B(4,4)$

$C(6,2)$

이제 다음 공식을 사용하여 모든 점 사이의 거리를 계산해야 합니다.

$d(A,B) = \sqrt{(4-2)^2+(4-1)^2 } = \sqrt{4+9} =\sqrt{13} = 3,61$

$d(A,C) = \sqrt{(6-2)^2+(2-1)^2 } = \sqrt{16+1} =\sqrt{17} = 4,12$

$d(B,C) = \sqrt{(6-4)^2+(2-4)^2 } = \sqrt{4+4} =\sqrt{8} = 2,83$

따라서 삼각형의 둘레는 세 변의 길이의 합이 됩니다.

$P=3,61+4,12+2,83= \bm{10,56}$

연습 4

꼭지점이 A, B, C인 삼각형이 이등변삼각형인지 확인하세요. 그러나 세 가지 요점은 다음과 같습니다.

$A(-4,5) \qquad B(7,-5) \qquad C(10,0)$

해결책 보기

삼각형이 이등변이 되려면 두 변의 길이가 같아야 합니다. 그러므로 우리는 꼭지점 사이의 거리에 해당하는 각 변의 길이를 찾아야 합니다.

따라서 삼각형의 꼭지점 사이의 거리를 계산합니다.

$d(A,B) = \sqrt{(7-(-4))^2+(-5-5)^2 } = \sqrt{11^2+(-10)^2} = \sqrt{221}$

$d(A,C) = \sqrt{(10-(-4))^2+(0-5)^2 } = \sqrt{14^2+(-5)^2} = \sqrt{221}$

$d(B,C) = \sqrt{(10-7)^2+(0-(-5))^2} = \sqrt{3^2+5^2} = \sqrt{34}$

따라서 삼각형에는 2개의 동일한 변이 있고 세 번째 변은 다른 두 변과 다르게 측정되므로 사실상 이등변삼각형입니다.

연습 5

다음 두 점에서 등거리에 있는 Y축의 점을 찾습니다.

$A(5,-3) \qquad \qquad B(-2,4)$

해결책 보기

우선, 점이 컴퓨터 축(OY 축)에 있으면 점의 가로좌표가 0임을 의미합니다.

$P(0,y)$

둘째, 점이 A와 B로부터 등거리에 있는 경우 이는 다음 방정식이 충족됨을 의미합니다.

$d(P,A)= d(P,B)$

따라서 두 점 사이의 거리 공식을 사용하면 이전 방정식에서 변수 y 의 값을 찾을 수 있습니다.

$\sqrt{(5-0)^2+(-3-y)^2 \vphantom{\frac{1}{2}}}=\sqrt{(-2-0)^2+(4-y)^2 \vphantom{\frac{1}{2}}}$

방정식의 양쪽에 근이 있으므로 단순화할 수 있습니다.

$5^2+(-3-y)^2=(-2)^2+(4-y)^2$

우리는 주목할 만한 힘과 평등(또는 주목할만한 제품)을 해결합니다.

$25+9+y^2+6y=4+16+y^2-8y$

그리고 알려지지 않은 y 값을 찾을 때까지 작업합니다.

$y^2+6y-y^2+8y=4+16-25-9$

$14y=-14$

$y=\cfrac{-14}{14}$

$y=-1$

간단히 말해서, 문제 설명이 우리에게 요구한 요점은 다음과 같습니다.

$\bm{P(0,-1)}$

이 기사가 유용했다면 점과 선 사이의 거리에 대한 연습 에도 관심이 있으실 것입니다. 링크된 페이지에는 단계별 연습문제뿐만 아니라 점과 선 사이의 거리 계산에 대한 자세한 설명, 다른 유형의 거리를 결정하기 위한 점과 선 사이의 거리 공식 적용 예 및 적용 방법도 나와 있습니다. .

두 점 사이의 거리를 구하는 공식은 무엇입니까?

두 점 사이의 거리를 계산하는 예

두 지점 사이의 거리 문제 해결

연습 1

연습 2

연습 3

연습 4

연습 5

댓글 달기 댓글 취소