▷ 두 벡터의 외적 계산(예)

이 페이지에서는 두 벡터의 외적(cross product)이 무엇인지, 그리고 계산 방법을 설명합니다. 또한 오른손 법칙(또는 코르크 따개)을 사용하여 외적의 방향과 방향을 찾는 방법도 살펴보겠습니다. 또한 이러한 유형의 작업의 사용법과 예제, 연습 문제 및 해결되는 문제를 단계별로 확인할 수 있습니다.

두 벡터의 외적은 무엇입니까?

수학에서 외적은 3차원 공간(R3)에서 두 벡터 사이의 연산입니다. 이 벡터 연산의 결과는 곱해진 두 벡터에 수직인 방향을 갖고 승수 벡터의 모듈과 이들이 형성하는 각도의 사인의 곱과 동일한 모듈을 갖는 벡터입니다. 즉, 그 공식은 다음과 같습니다.

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha)$

이전 공식에서 볼 수 있듯이 교차곱은 다음과 같이 표시됩니다.

$\bm{\times}$

, 이것이 교차곱(cross product)이라고도 불리는 이유입니다. Gibbs 벡터 곱이라고도 합니다. 그가 발명했기 때문입니다.

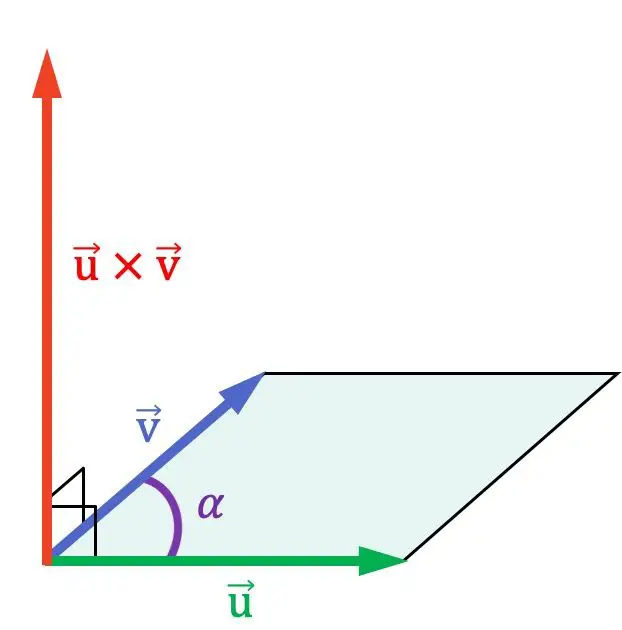
이전 그래픽 표현에서 볼 수 있듯이 외적은 두 벡터가 곱하는 두 벡터에 수직이므로 이를 포함하는 평면에 수직입니다.

두 벡터의 외적을 계산하는 공식

벡터의 데카르트 좌표를 알고 있는 경우 외적을 계산하는 가장 간단한 방법은 3×3 행렬식을 구하는 것입니다. 어떻게 완료되었는지 확인하세요.

두 벡터를 고려하십시오.

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

벡터 곱은 다음과 같습니다.

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}$

벡터는 어디에

$\vv{i}, \vv{j},\vv{k}$

이는 각각 X, Y 및 Z 축 방향의 단위 벡터입니다.

두 벡터 간의 외적을 계산하는 방법의 예를 살펴보겠습니다.

$\vv{\text{u}}= (3,1,0) \qquad \vv{\text{v}}= (2,1,-1)$

벡터 간의 벡터 곱을 결정하려면 다음과 같은 차수 3의 행렬식을 만들어야 합니다.

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}$

이 경우, 우리는 보조 인자나 보조 인자로 행렬식을 풀 것입니다(사루스 규칙(Sarrus rule)도 사용될 수 있습니다):

$\begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}$

따라서 두 벡터의 벡터 곱의 결과는 다음과 같습니다.

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-1,3,1)}$

외적의 방향과 방향을 결정합니다.

때로는 외적의 결과인 벡터의 구성 요소를 알 필요가 없지만 해당 모듈, 방향 및 방향을 찾는 것으로 충분합니다. 이는 물리학, 특히 힘 계산에서 자주 발생합니다.

따라서 벡터 곱의 방향과 방향을 찾는 데는 몇 가지 규칙이 있으며, 가장 잘 알려진 것은 세 손가락이나 손 전체를 사용하는 오른손 법칙 과 코르크 따개 법칙(또는 나사) 입니다. 그 중 무엇이든 사용할 수 있으므로 모두 알 필요는 없습니다. 가장 좋아하는 규칙을 고수할 수 있도록 세 가지 규칙을 설명하겠습니다. 😉

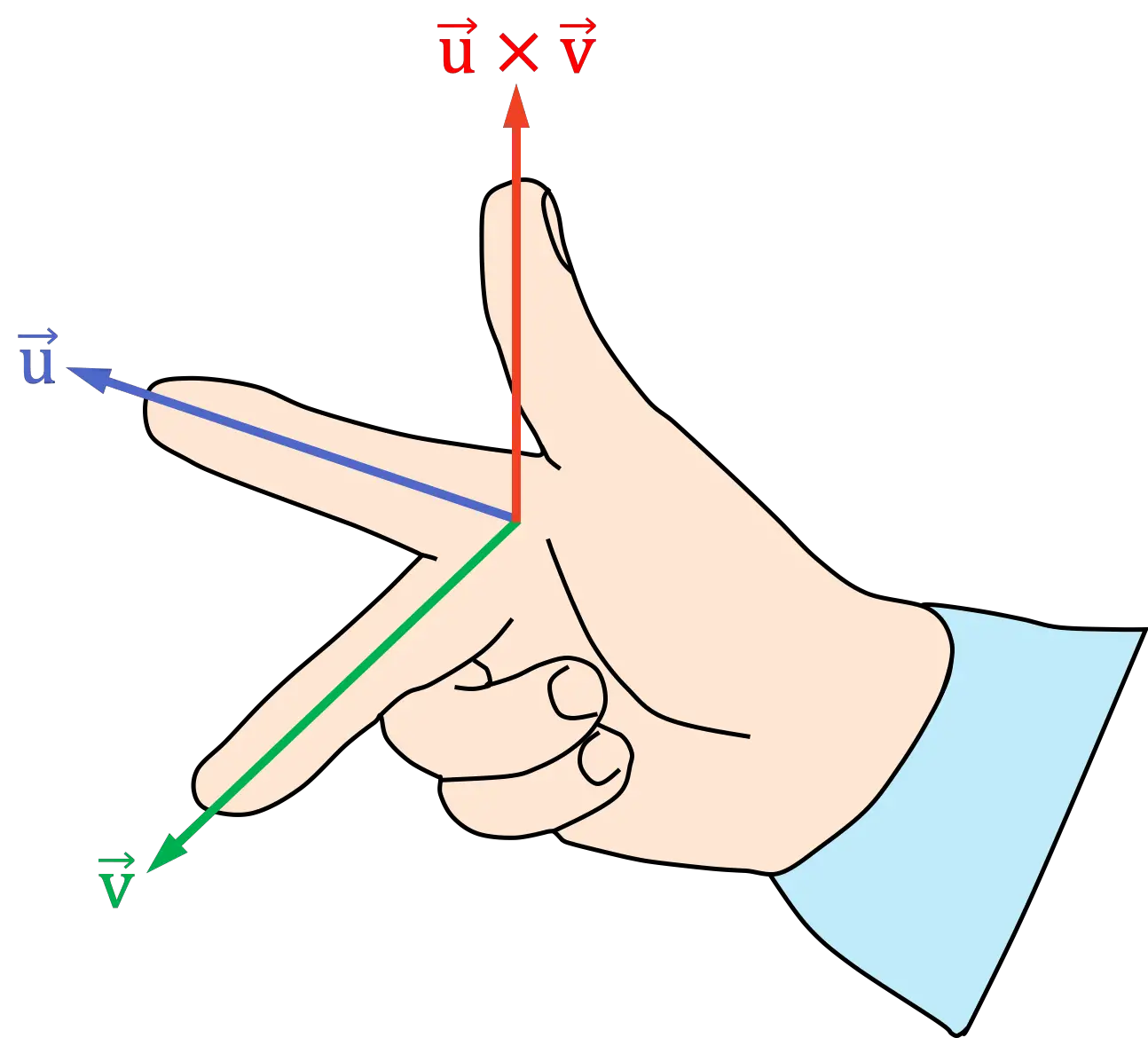
오른손 법칙(3손가락)

오른손 법칙 또는 법칙의 세 손가락 버전에는 다음 단계를 수행하는 작업이 포함됩니다.

교차곱의 첫 번째 벡터를 향해 오른손 검지를 놓습니다.
$(\vv{\text{u}}).$
오른손의 중지(또는 중지)를 외적의 두 번째 벡터 방향으로 놓습니다.
$(\vv{\text{v}}).$
결과 엄지손가락 위치는 외적의 방향과 방향을 나타냅니다.
$(\vv{\text{u}}\times\vv{\text{v}}).$

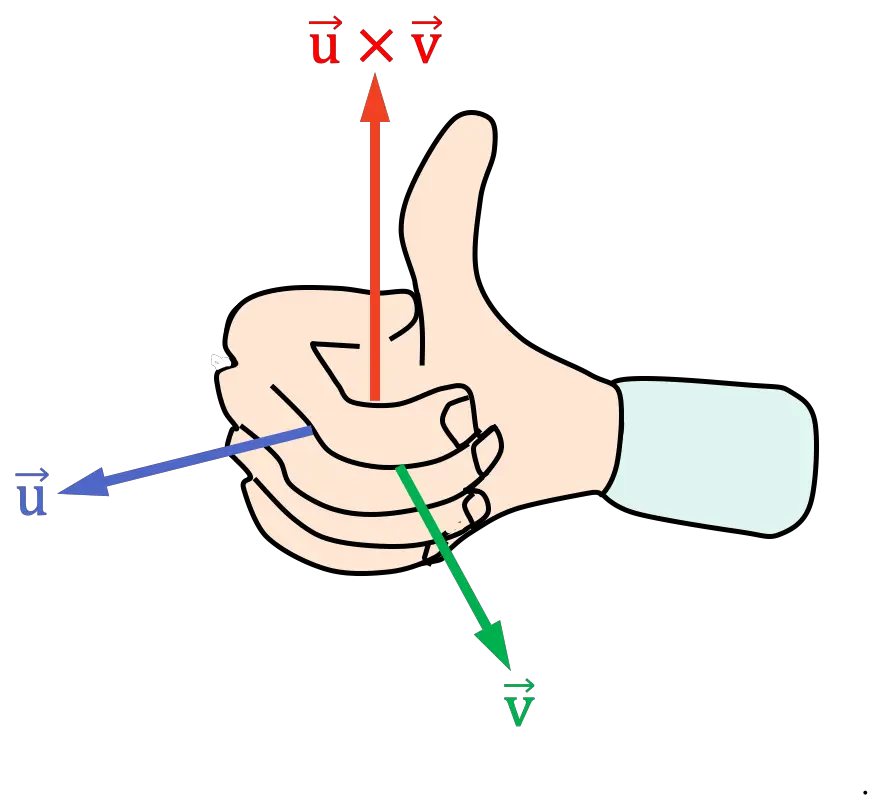
오른손 법칙(손바닥)

오른손 법칙 또는 법칙의 손바닥 버전은 이전 규칙과 매우 유사합니다. 적용하려면 다음 단계를 따라야 합니다.

외적의 첫 번째 벡터와 같은 방향을 손가락으로 가리키는 오른손을 놓습니다.
$(\vv{\text{u}}).$
교차곱의 두 번째 벡터를 향해 손가락을 움직여 오른손을 닫습니다.
$(\vv{\text{v}}).$

벡터 사이의 각도(또는 거리)가 더 작은 쪽에서 손을 닫아야 합니다.
엄지손가락의 결과 위치에 따라 외적의 방향이 결정됩니다.
$(\vv{\text{u}}\times\vv{\text{v}}).$

코르크 따개 규칙

코르크 따개 또는 나사 규칙은 손바닥 전체를 사용하는 오른손 규칙과 유사합니다. 절차는 다음과 같습니다.

상상력을 발휘하여 외적의 첫 번째 벡터와 같은 방향을 가리키는 손잡이가 있는 코르크 따개(또는 나사)를 배치합니다.
$(\vv{\text{u}}).$
그런 다음 코르크 마개를 외적의 두 번째 벡터 방향으로 돌립니다.
$(\vv{\text{v}})$

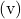
마치 코르크에 넣으려는 것처럼. 벡터 사이의 거리가 가장 짧은 쪽으로 코르크 마개를 돌려야 합니다.
코르크 마개나선이 가리키는 방향이 벡터산물의 방향과 방향이 됩니다.
$(\vv{\text{u}}\times\vv{\text{v}}).$

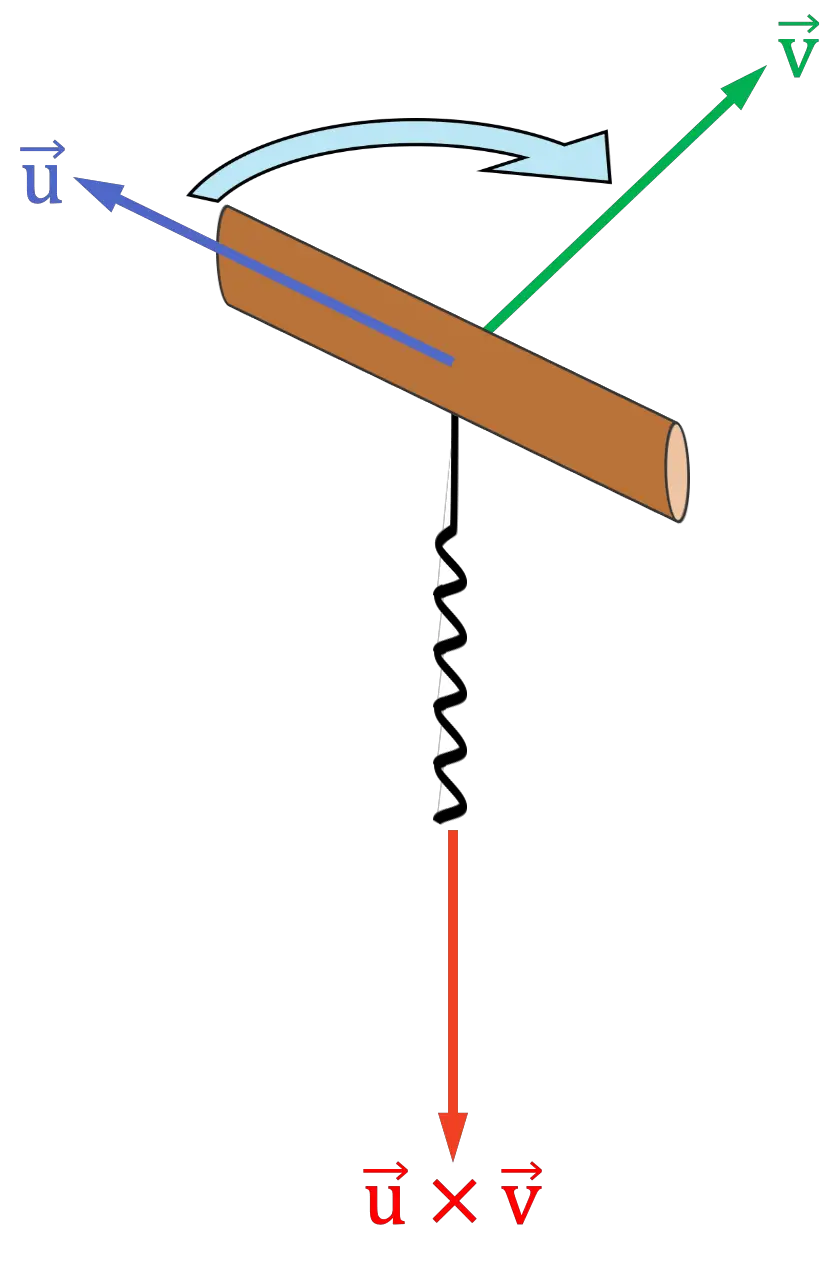
두 벡터의 외적 속성

두 벡터의 외적은 다음과 같은 특징을 갖습니다.

반교환 특성: 벡터 곱에 포함된 벡터의 순서는 그에 따라 부호가 달라지므로 무관심하지 않습니다.

$\vv{\text{u}}\times\vv{\text{v}} = - \vv{\text{v}}\times\vv{\text{u}}$

벡터의 덧셈과 뺄셈에 관한 분배법칙 :

$\vv{\text{u}}\times(\vv{\text{v}}+\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}+\vv{\text{u}}\times \vv{\text{w}}$

$\vv{\text{u}}\times(\vv{\text{v}}-\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}-\vv{\text{u}}\times \vv{\text{w}}$

동질성 : 외적의 벡터에 스칼라(실수)를 곱하는 것은 외적의 결과에 해당 스칼라를 곱하는 것과 동일합니다.

$k \cdot (\vv{\text{u}}\times\vv{\text{v}}) = (k\cdot \vv{\text{u}})\times\vv{\text{v}}=\vv{\text{u}}\times(k\cdot\vv{\text{v}})$

벡터 곱의 결과인 벡터는 연산에 포함된 두 벡터에 수직 입니다.

$\begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}$

또한 두 벡터가 직교하는 경우 다음 방정식이 충족됩니다.

$\vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}$

두 평행 벡터 의 외적은 0 벡터(또는 0)와 같습니다.

$\vv{\text{u}} \ || \ \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}}\times\vv{\text{v}}=0$

두 벡터가 이루는 각도를 모르는 경우 벡터 곱의 계수는 다음 식을 사용하여 계산할 수도 있습니다.

$\lvert \vv{\text{u}}\times\vv{\text{v}} \rvert = \sqrt{ \lvert \vv{\text{u}}\rvert ^2 \cdot \lvert \vv{\text{v}} \rvert ^2 - (\vv{\text{u}}\cdot \vv{\text{v}})^2 \vphantom{\frac{1}{2}}$

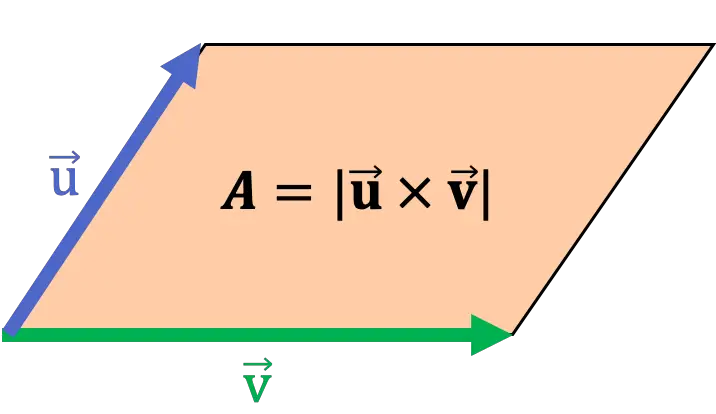
외적을 사용하여 평행사변형이나 삼각형의 면적을 계산합니다.

기하학적으로 두 벡터의 외적 계수는 두 벡터를 변으로 갖는 평행사변형의 면적과 일치합니다. 따라서 외적을 사용하여 평행사변형의 면적을 계산할 수 있습니다.

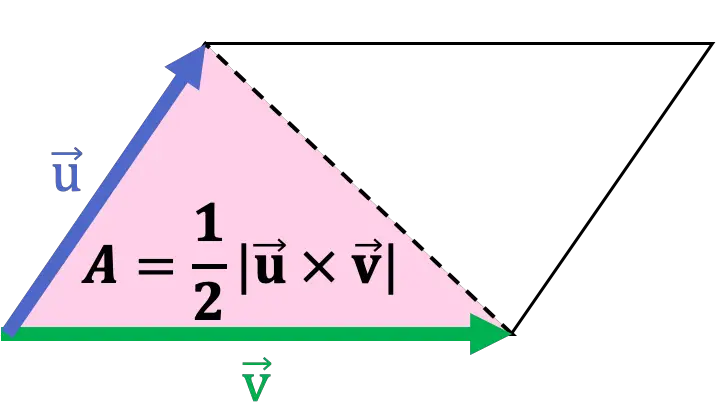
또한 평행사변형의 대각선은 평행사변형을 두 개의 삼각형으로 나눕니다. 즉, 삼각형은 평행사변형의 절반입니다. 따라서 삼각형의 면적은 두 변을 벡터로 사용하는 외적 계수의 절반입니다.

3차원 공간에서 벡터의 모듈러스는 해당 좌표의 제곱합의 근입니다.

$\lvert \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

이것은 수학 분야에서 두 벡터의 외적을 적용하는 두 가지 예입니다. 그러나 여전히 다른 용도로 사용됩니다. 예를 들어 물리학에서는 자기장을 계산하는 데 사용됩니다.

벡터의 벡터 제품에 대한 연습 문제 해결

연습 1

다음 두 벡터 간의 외적을 계산합니다.

$\vv{\text{u}}= (-1,4,2) \qquad \vv{\text{v}}= (0,-2,1)$

솔루션 보기

벡터 간의 벡터 곱을 결정하려면 다음과 같은 차원 3×3의 행렬식을 풀어야 합니다.

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}$

이 경우, 우리는 보조 인자나 보조 인자에 의해 행렬식을 풀 것입니다(그러나 Sarrus 규칙도 사용될 수 있습니다):

$\begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}$

따라서 두 벡터의 벡터 곱의 결과는 다음과 같습니다.

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(8,1,2)}$

연습 2

다음 두 벡터 사이의 외적을 구합니다.

$\vv{\text{u}}= (3,-2,4) \qquad \vv{\text{v}}= (1,5,-3)$

솔루션 보기

두 벡터 간의 벡터 곱을 찾으려면 다음 3×3 행렬식을 풀어야 합니다.

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}$

이 경우 우리는 행렬식을 수반 또는 보조 인자로 풀 것입니다(Sarrus의 규칙은 서로 바꿔서 사용할 수 있음).

$\begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}$

따라서 두 벡터 사이의 벡터 곱의 결과는 다음과 같습니다.

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-14,13,17)}$

연습 3

두 벡터의 모듈과 그들이 형성하는 각도를 아는 것:

$|\vv{\text{u}}|= 5 \qquad |\vv{\text{v}}|= 6 \qquad \alpha = 30º$

두 벡터의 외적 크기를 결정합니다.

솔루션 보기

다음 공식을 적용하여 두 벡터 사이의 벡터 곱의 계수를 쉽게 계산할 수 있습니다.

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}$

연습 4

화면 평면에 포함된 다음 벡터에서:

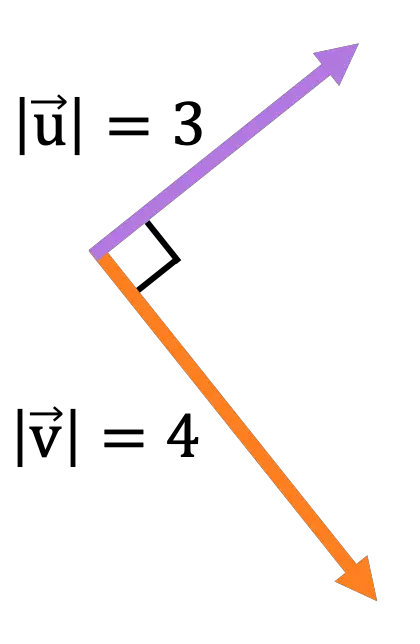
다음 벡터 연산으로 인해 발생하는 벡터의 크기, 방향 및 의미를 계산합니다.

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert$

솔루션 보기

두 벡터는 수직이므로 벡터 곱의 노름은 다음과 같습니다.

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}$

반면, 벡터 곱의 결과인 벡터는 작업에 참여하는 두 벡터에 수직이므로 그 방향은 화면에 수직이 됩니다.

그리고 마지막으로 직선(또는 코르크 따개) 규칙을 사용하여 결과 벡터의 방향이 화면 내부를 향할 것임을 추론할 수 있습니다.

연습 5

두 변으로 다음 벡터를 갖는 평행사변형의 면적을 계산합니다.

$\vv{\text{u}}= (2,3,-2) \qquad \vv{\text{v}}= (5,0,-1)$

솔루션 보기

평행사변형의 면적은 이를 형성하는 벡터의 외적 계수와 일치합니다. 따라서 우리는 벡터의 벡터 곱을 계산합니다.

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}$

그런 다음 모듈은 다음과 같습니다.

$A=\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-3)^2+(-8)^2+(-15)^2}=\bm{17,26} \ \mathbf{u}\bm{^2}$

연습 6

정점이 다음 점인 삼각형의 면적을 찾으십시오.

$A(2,1,0) \qquad B(4,0,3)\qquad C(-1,2,3)$

솔루션 보기

먼저 삼각형의 변을 구성하는 벡터를 계산해야 합니다.

$\vv{AB} = B- A = (4,0,3)-(2,1,0) = (2,-1,3)$

$\vv{BC} =C- B =(-1,2,3)- (4,0,3) = (-5,2,0)$

삼각형의 면적은 그것을 형성하는 벡터의 벡터 곱 크기의 절반입니다. 따라서 우리는 벡터의 벡터 곱을 계산합니다.

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}$

모듈 이후:

$\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-6)^2+(-15)^2+(-1)^2}=16,19$

마지막으로 삼각형의 면적은 모듈의 절반이 됩니다.

$A=\cfrac{1}{2}\cdot \lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \cfrac{1}{2}\cdot 16,19=\bm{8,09} \ \mathbf{u}\bm{^2}$

두 벡터의 외적(또는 외적)

두 벡터의 외적은 무엇입니까?

두 벡터의 외적을 계산하는 공식

외적의 방향과 방향을 결정합니다.

오른손 법칙(3손가락)

오른손 법칙(손바닥)

코르크 따개 규칙

두 벡터의 외적 속성

외적을 사용하여 평행사변형이나 삼각형의 면적을 계산합니다.

벡터의 벡터 제품에 대한 연습 문제 해결

연습 1

연습 2

연습 3

연습 4

연습 5

연습 6

댓글 달기 댓글 취소