단일 행렬 - Mathority

이 페이지에서는 단위 행렬이 무엇인지 설명하고, 또한 잘 이해할 수 있도록 몇 가지 연습 문제를 통해 설명합니다. 또한 선형 대수학에 매우 중요한 이러한 유형의 행렬의 모든 속성이 무엇인지도 알게 될 것입니다.

단일 행렬이란 무엇입니까?

유니터리 행렬의 정의는 다음과 같습니다.

유니타리 행렬은 켤레 전치 행렬을 곱하면 단위 행렬이 되는 복소 행렬입니다. 즉, 다음 조건이 충족됩니다.

$U\cdot U^* = U^* \cdot U =I$

금

$U$

는 단일 행렬이고

$U^*$

공액 전치입니다.

따라서 이 조건은 단위 행렬의 역행렬이 켤레 전치임을 의미합니다. 왜냐하면 역행렬의 정의에 따르면 해당 행렬의 곱이 행렬 d’identify와 동일한 경우 행렬은 다른 행렬의 역행렬이기 때문입니다. .

$\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}$

따라서 유니타리 행렬은 항상 역행렬을 갖기 때문에 항상 정규 또는 비퇴화 행렬이 됩니다.

반면, 실수 환경에서 유니타리 행렬의 유사체는 직교 행렬 이며, 이 경우 유니타리 행렬에 전치를 곱한 것이 단위 행렬과 같다는 것은 사실입니다.

$U\cdot U^t = U^t \cdot U =I$

따라서 이 경우 U의 역행렬은 바로 전치된(또는 전치된) 행렬이 됩니다.

단위 행렬의 예

차원 2×2의 단위 행렬의 예

단위 행렬의 개념을 살펴본 후에는 이를 잘 이해하기 위해 2×2 단위 행렬의 예를 살펴보겠습니다.

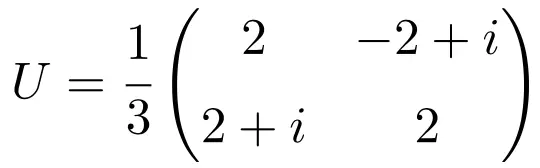
이 행렬은 켤레 행렬을 곱하면 단위(또는 단위) 행렬이 되기 때문에 단일 행렬입니다.

$\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

그리고 이전에 살펴본 것처럼 모든 단일 행렬은 켤레 전치를 사용하여 교환 가능합니다.

$\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

단위 대각선 행렬의 예

복소수 i 로만 구성된 대각행렬 역시 행렬의 차원에 관계없이 유니타리 행렬의 한 예입니다. 아래에는 차원 3 × 3의 단위 행렬을 사용하여 이를 설명하는 해결된 연습이 있습니다.

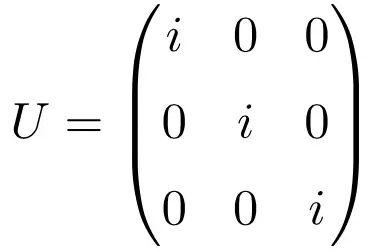
켤레 전치로 행렬의 곱을 풀면 단위 행렬이 해로 제공됩니다.

$\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}$

행렬을 역으로 곱해도 같은 일이 발생합니다.

$\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}$

이 행렬의 특징은 행렬이 주대각선의 허수 i 에 의해 형성될 때마다 나머지 요소가 0(0)이기 때문에 모든 차원의 단일 행렬의 예 역할을 한다는 것입니다. ) 그것은 단일 행렬이 될 것입니다.

단일 행렬의 속성

단위 행렬의 속성은 다음과 같습니다.

분명히 모든 단일 행렬은 일반 행렬 입니다. 모든 일반 행렬이 단일 행렬은 아니지만

단위 행렬은 항상 정사각 행렬 입니다.

모든 단위 행렬은 대각화 가능합니다. 즉, 대각 행렬로 변환될 수 있습니다.

단위 행렬의 행렬식의 절대값은 항상 1과 같습니다.

$\begin{vmatrix} det(U) \end{vmatrix} = 1$

동일한 행렬은 단일 행렬입니다.

모든
$n$

, 모든 단위 행렬의 집합

$n\times n$

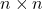
매트릭스 제품 작업을 통해 단위 그룹이라는 그룹을 형성합니다.

따라서 동일한 차수의 두 단위 행렬을 곱하면 또 다른 단위 행렬이 생성됩니다.

단위 행렬의 모든 고유값(또는 고유값)의 계수는 항상 1과 같습니다.

$\begin{vmatrix} \lambda \end{vmatrix} = 1$

이 유형의 행렬의 고유공간은 직교합니다.

단일 행렬이란 무엇입니까?

단위 행렬의 예

차원 2×2의 단위 행렬의 예

단위 대각선 행렬의 예

단일 행렬의 속성

댓글 달기 댓글 취소