단리는 이자를 계산하는 가장 일반적인 방법으로, 주택 구입부터 개인 대출까지 다양한 목적으로 사용됩니다. 단리를 계산해야 하는 경우 이 가이드에서 단계별로 이자를 계산하는 방법을 알려드립니다. 우리는 또한 귀하의 작업을 더 쉽게 할 수 있도록 온라인 계산기를 제공합니다.
단순이자 계산기
이 온라인 단리 계산기는 단리 계산과 관련된 모든 변수를 계산하는 데 도움이 되는 도구입니다. 이를 사용하려면 계산하려는 항목을 선택하고 해당 항목이 요구하는 변수에 대한 데이터를 입력하기만 하면 됩니다. 그런 다음 계산 버튼을 클릭하면 됩니다.
단순이자란 무엇인가요?
단리란 일정 기간 동안 금액을 투자하거나 대출할 때 부과되는 이자율입니다. 초기금액에 이자율과 시간을 곱하여 계산됩니다. 요약하자면, 이 이자는 지속적이고 일반적으로 단기적인 금융 활동에 사용됩니다.
이자율과 기간이 일정하게 유지되므로 이자가 증가하지 않으므로 매월 또는 매년 지불해야 하는 이자는 항상 동일 합니다. 이것이 단리와 복리 의 주요 차이점입니다.
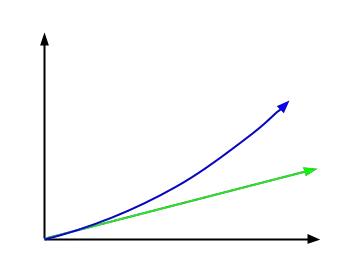
다음 이미지에서는 녹색으로 단리를 나타내는 함수와 파란색으로 표시된 복리 함수를 볼 수 있습니다. 이미지에서 볼 수 있듯이 훨씬 더 기하급수적인 모양을 가지고 있습니다.
단리 이자를 계산하는 공식
단리 계산 공식은 I = C xixt 이며 여기에는 다음 변수가 포함됩니다.
- 초기자본금(C): 투자 또는 대출한 금액으로 단리 이자가 계산됩니다.
- 이자율(i): 이 지표는 시간에 따른 이자 금액을 백분율로 알려줍니다. 수식에 1만큼 적는 것이 중요합니다(백분율 값을 100으로 나눕니다).
- 시간(t): 투자 기간의 길이로, 일반적으로 연 단위로 표시됩니다. 하지만 아래에서는 이를 월, 일과 같은 다른 시간 단위로 변환하는 방법을 설명합니다.
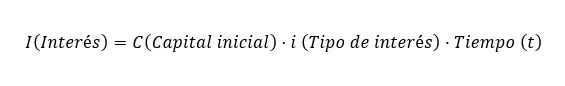
이 공식이 어떻게 사용되는지 보기 위해 다음 예를 고려해 볼 수 있습니다. 연간 4%의 이율로 €1000를 투자했는데, 3년 후에 얼마나 많은 이자를 창출하게 될까요? 생성된 이자를 찾으려면 다음 공식을 적용해야 합니다. I = C x (i ¼ 100) xt = 1000 x (4 ¼ 100) x 3 = €120.
그런 다음 기본 공식에서 다양한 변수를 분리할 수 있으므로 초기 자본금, 이자율, 시간 및 최종 자본을 계산할 수 있는 공식을 얻을 수 있습니다. 이는 다음 섹션에서 볼 수 있으며, 이미 본 공식과 또 다른 매우 간단한 공식에서 이러한 변수를 계산하는 방법을 알려줄 것입니다.
최종 자본금은 어떻게 계산되나요?
최종 자본금을 계산하려면 논리를 적용하면 됩니다. 그런 다음 최종 금액이 초기 금액과 동일하므로 이자를 적용하면 공식은 최종 자본금(Cf) = 초기 자본금(C) + 이자(I)입니다. 이 표현식은 두 번째로 중요한 단리 공식이며, 가장 중요한 것은 이전 공식입니다.
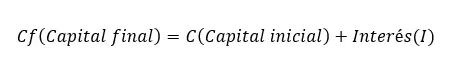
이제 공식을 알았으므로 다음 실제 예를 풀어 보십시오. 4년 동안 €50,000를 투자하고 €20,000의 이자를 얻을 경우 얻을 수 있는 최종 자본은 얼마입니까? 간단히 말해서 이전의 표현식을 적용합니다: 최종 자본(Cf) = 초기 자본(C) + 이자(I) = 50,000 + 20,000 = €70,000.
초기 자본금은 어떻게 계산되나요?
초기 자본금을 계산하려면 제공되는 데이터에 따라 두 가지 공식을 사용할 수 있습니다. 첫째, 최종 자본과 이자로 발생한 금액이 있는 경우 이전 섹션의 표현식을 적용할 수 있습니다. 초기 자본(C) = 최종 자본(Cf) – 이자(I).
둘째, 초기 자본의 가치를 단순 이자 공식(처음에 이야기한 것)으로 분리할 수 있습니다. 따라서 초기 자본금(C) = 이자(I) ¼(시간(t) x 이자율(i))이 남게 됩니다.

더 복잡한 두 번째 사례의 예를 살펴보겠습니다. 2년 동안 8%의 이율로 €30,000에 대한 이자를 얻으려면 얼마를 투자해야 합니까? 초기 자본 = I ¼ (tx (i ¼ 100)) 공식을 적용하면 초기 자본금은 30,000 ¼ (2 x (8 ¼ 100)) = €187,500이 됩니다.
이자율은 어떻게 계산되나요?
이자율을 계산하려면 간단한 이자 공식도 사용해야 하지만 i를 분리해야 합니다. 따라서 이자율(i) = 이자(I) ¼ (초기자본금(C) x 시간(t))이 남습니다. 보시다시피 모든 수식은 동일하지만 다른 변수를 분리합니다.
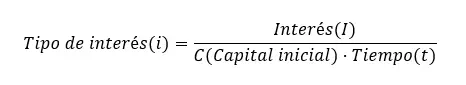
다음은 이자율을 계산하는 실제 사례입니다. €180,000를 5년 동안 €200,000로 전환하려면 어떤 이자율로 투자해야 합니까? 이 예에서는 먼저 이자를 찾아야 합니다. I = Cf – C = 200,000 – 180,000 = €20,000. 그런 다음 이자율 = 20,000 ¼ (180,000 x 5) = 0.022 x 100 = 2.2%를 해결합니다.
시간은 어떻게 계산되나요?
마지막으로 시간을 계산할 수 있는데, 이는 초기 공식인 시간(t) = 이자(I) ¼(초기 금액(C) x 이자율(i))에서도 얻을 수 있습니다. 공식에서는 시간 단위가 연도여야 한다는 점을 기억하는 것이 중요합니다. 그러나 다른 단위로 표현하려면 다음과 같은 공식 변형을 사용할 수 있습니다.
- I = C · (i / 100) · t가 연도인 경우 (일반식)
- I = C · (i / 1200) · t가 월인 경우 (결과는 월)
- I = C · (i / 36000) · t t가 일인 경우 (결과는 일수)
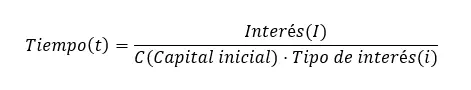
다음 예를 보십시오. 5%의 이율로 €5,000의 이자를 창출하기 위해 €40,000의 투자를 원한다면 얼마나 많은 시간이 지나야 합니까? 계산은 다음과 같습니다: 시간 = 5,000 ¼ (40,000 x 5 ¼ 100) = 2.5년. 그러나 이를 월 단위로 계산하려면 다음과 같이 하면 됩니다. 시간 = 5,000 ¼ (40,000 x 5 ¼ 1200) = 30개월.
단리 계산의 실제 예
이제 단리 공식을 구성하는 각 변수를 계산하는 예를 살펴보았습니다. 그러나 우리는 가장 일반적인 계산 , 즉 관심을 끄는 계산의 마지막 예를 보여드리고 싶습니다. 첫 번째 공식을 적용하면 남은 부분이 생깁니다. 계산을 검토하려는 경우 사례 연구는 다음과 같습니다.
우리는 투자하기 위해 €10,000를 빌렸고 그들이 우리에게 연 3%의 이자를 요구할 경우 5년 후에 얼마나 많은 돈을 갚아야 하는지 계산하려고 합니다. 계산은 다음과 같습니다.
10,000 x 0.03 = 300
300 x 5년 = €1,500
CF = €10,000 + €1,500 = €11,500
따라서 5년 후 이자는 €1,500가 되고 최종 지불 자본금은 €11,500가 됩니다 .
결론
정리하자면, 단리를 계산 하려면 대출금액, 이자율, 기간 등을 고려해야 합니다. 거기에서 이 세 숫자를 곱하면 총 지불 이자 금액을 얻을 수 있습니다. 그리고 이자 대신 다른 변수 중 하나를 계산하려면 일반 공식에서 해당 값을 분리하면 됩니다.