이 페이지에서는 다항식의 추가가 수행되는 방법에 대한 설명을 찾을 수 있습니다. 또한, 다항식의 합 예시와 단계별로 풀어보는 연습문제도 볼 수 있습니다. 마지막으로 다항식을 사용한 이러한 유형의 연산의 속성이 무엇인지 설명합니다.
다항식을 추가하는 방법은 무엇입니까?
수학에서 두 개 이상의 다항식을 더하려면, 유사한 다항식의 항을 함께 더해야 합니다. 즉, 다항식을 추가하는 것은 동일한 리터럴 부분(동일한 변수 및 동일한 지수)을 갖는 항을 추가하는 것으로 구성됩니다.
따라서 다항식의 합은 두 가지 다른 방법, 즉 수직 방법과 수평 방법으로 수행될 수 있습니다. 아래에는 두 절차에 대한 설명이 나와 있지만 다항식을 수직으로 더하는 방법을 먼저 배우고 수평 방법으로 넘어가는 것이 좋습니다. 분명히 당신이 선호하는 것을 고수하십시오.
수직 다항식 추가하기
다음으로 예제를 사용하여 두 개의 다항식을 수직으로 추가하는 방법을 살펴보겠습니다.
- 다음 두 다항식을 추가합니다.
![]()
![]()
가장 먼저 해야 할 일은 하나의 다항식을 다른 다항식 아래에 배치하여 두 다항식의 동일한 항이 열별로 정렬되도록 하는 것입니다.
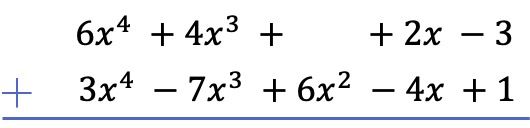
경고: 다항식에 특정 차수의 항이 없으면 공간을 비워 두어야 합니다. 예를 들어
![]()
2차 단항식이 없기 때문에 사이트에 빈 공간이 있습니다.
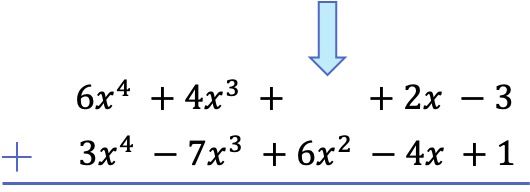
모든 항을 가장 높은 차수에서 가장 낮은 차수까지 순서대로 배열한 후 리터럴 부분을 동일하게 유지하면서 각 열에 계수를 추가합니다.
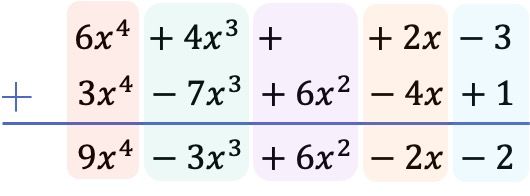
결과적으로 2개의 다항식의 합으로 얻은 결과는 다음과 같습니다.
![]()
이제 다항식의 덧셈을 이해했으므로 다항식으로 구성된 분수를 덧셈할 수도 있다는 것을 알아두십시오. 이러한 유형의 연산을 대수 분수 덧셈 이라고 합니다. 이 링크를 클릭하면 대수 분수의 합을 계산하는 방법뿐만 아니라 대수 분수를 사용한 모든 연산을 해결하는 방법도 알아볼 수 있습니다.
다항식의 수평 덧셈
방금 다항식을 세로로 더하는 방법을 살펴봤지만 이제 다항식을 더하는 또 다른 방법, 즉 가로로 다항식을 더하는 방법을 살펴보겠습니다. 확실히 이 절차는 이전 절차보다 빠르지만 다항식의 개념을 더 잘 숙지하는 것이 필요합니다.
그럼 예를 통해 다항식을 추가하는 이 방법이 무엇으로 구성되어 있는지 살펴보겠습니다. 두 방법의 차이점을 확인할 수 있도록 이전 예제와 동일한 다항식을 추가하겠습니다.
- 다음 두 다항식의 합을 계산합니다.
![]()
![]()
먼저 동일한 작업에서 두 다항식을 차례로 배치해야 합니다.
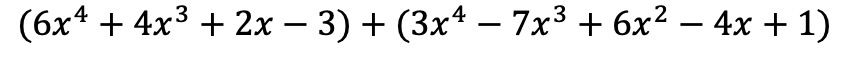
그리고 이제 동일한 문자 부분을 갖는 용어, 즉 동일한 변수(문자)와 동일한 지수를 갖는 용어를 추가합니다. 유사하지 않은 용어는 추가할 수 없습니다.
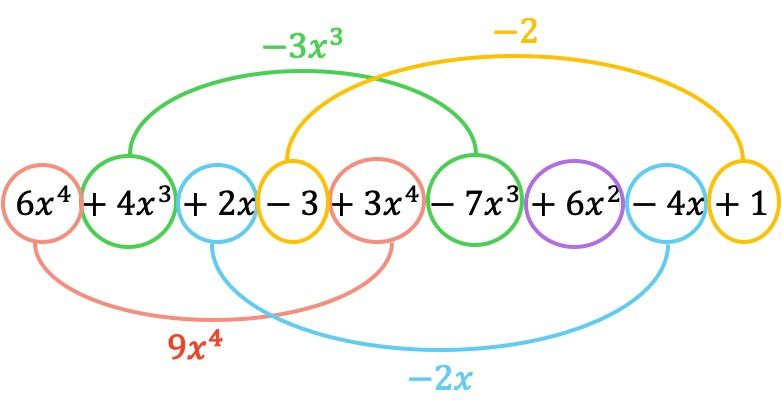
따라서 덧셈으로 인한 다항식은 다음과 같습니다.

보시다시피 두 방법 모두에서 동일한 결과를 얻었으므로 다항식을 추가할 때 가장 적합한 방법을 사용할 수 있습니다.
다항식 추가 문제 해결
연습할 수 있도록 다항식 합의 몇 가지 문제를 풀어보겠습니다. 궁금하신 점은 페이지 댓글로 질문해주시면 최대한 빨리 답변해드리겠습니다.
연습 1
다음 두 다항식을 추가합니다.
![]()
![]()
이 경우 두 개의 다항식을 수직으로 추가하겠습니다. 이를 위해 다항식을 차수별로 정렬하고 동일한 열에 있는 단항식을 추가합니다.
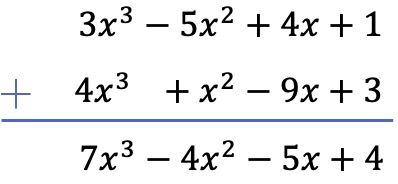
연습 2
다음 두 다항식의 합을 푼다:
![]()
![]()
수직법을 사용하여 두 다항식의 합을 계산합니다. 따라서 우리는 다항식을 차수별로 정렬하고 동일한 열에 있는 항을 추가합니다.
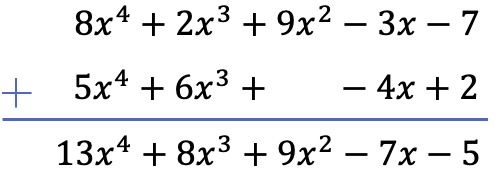
이 특별한 경우에는 2차 항이 없기 때문에 두 번째 다항식의 2차 열에 공백을 남겨 두어야 합니다.
연습 3
다음 두 다항식의 합은 얼마입니까?
![]()
![]()
수직법을 사용하여 두 다항식의 덧셈을 수행하겠습니다. 그래서:
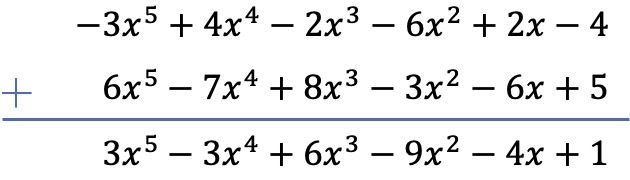
연습 4
다음 세 가지 다항식의 합을 계산합니다.
![]()
![]()
![]()
수직법을 사용하여 3개의 다항식의 합을 계산합니다. 따라서 다항식을 차수별로 정렬하고 같은 열에 있는 항을 추가합니다.
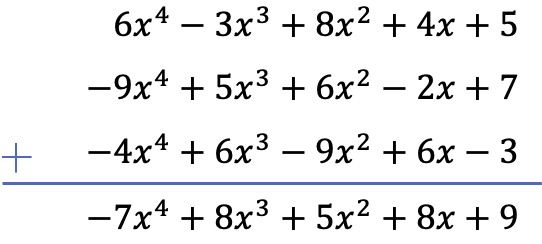
👉👉👉이제 두 개의 다항식이 어떻게 합해지는지 보았으므로 다항식의 또 다른 특징적인 연산인 공통 인수에 관심이 있을 것입니다. 다항식에서 공통인수를 추출하는 것은 매우 복잡하고 이해하기 어렵습니다. 실제로 이 작업을 수행할 때 많은 실수가 발생합니다. 그렇기 때문에 공약수 추출 방법을 단계별로 설명하는 가이드를 준비했습니다. 이를 통해 완벽하게 이해하고 이 작업을 수행할 때 실수하지 않도록 하세요. 링크를 클릭하여 다항식에서 공통인수를 추출하는 팁이 무엇인지 알아보세요.
다항식 덧셈의 속성
다항식의 합은 다음과 같은 특징을 갖습니다.
- 결합 속성 : 3개 이상의 다항식을 더할 때 결과는 항상 동일하므로 다항식을 어떻게 그룹화해도 상관 없습니다. 즉, 다음과 같은 동등성이 확인됩니다.
![]()
- 교환 특성 : 다항식의 덧셈에서 덧셈의 순서는 덧셈의 결과를 수정하지 않습니다.
![]()
- 중립 요소 : 분명히 다항식과 숫자 값이 0인 다른 다항식을 더하는 것은 첫 번째 다항식과 동일합니다.
![]()
- 반대 요소 : 다항식과 그 반대 다항식을 더한 결과는 항상 0입니다.
![]()
설명에 대해 어떻게 생각하시나요? 이 정보가 도움이 되었나요? 다항식을 추가하는 방법 중 수직 또는 수평 중 어떤 방법을 선호합니까? 댓글에서 여러분의 의견을 읽었습니다! 🙌