이 페이지에서는 다항식을 뺄셈하는 방법을 설명합니다. 또한 다항식 뺄셈에 대한 몇 가지 예와 해결된 단계별 연습을 찾을 수 있습니다.
다항식을 빼는 방법은 무엇입니까?
두 다항식을 빼려면, 비슷한 다항식의 항을 빼야 합니다. 즉, 다항식의 뺄셈은 동일한 리터럴 부분(동일한 변수 및 동일한 지수)을 갖는 항의 뺄셈으로 구성됩니다.
수학에서는 수직법과 수평법이라는 두 가지 방법으로 다항식의 뺄셈을 계산할 수 있습니다. 아래에는 두 절차에 대한 설명이 나와 있지만 먼저 수직으로 다항식을 뺀 다음 수평 방법으로 넘어가는 방법을 배우는 것이 좋습니다. 분명히 당신이 선호하는 것을 고수하십시오.
수직 다항식의 뺄셈
다음으로, 예제를 사용하여 두 다항식을 수직으로 뺄셈하는 방법을 살펴보겠습니다.
- 뺄셈을 해라
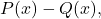
두 개의 다항식이 되는 것:
![]()
![]()
다항식 뺄셈을 찾기 위해 가장 먼저 해야 할 일은 하나의 다항식을 다른 다항식 아래에 배치하여 두 다항식의 동일한 항이 열에 정렬되도록 하는 것입니다.
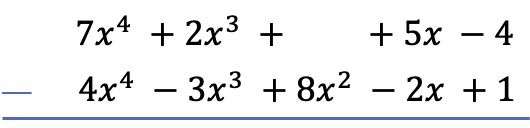
경고: 다항식에 특정 차수의 항이 없으면 공간을 비워 두어야 합니다. 예를 들어, 다항식
![]()
2차 단항식이 없으므로 그 자리에 빈 공간이 있습니다.
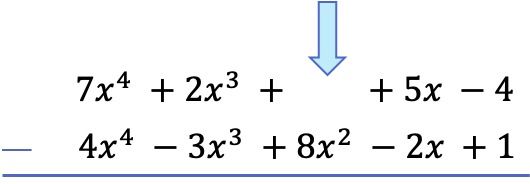
이제 다항식을 직접 뺄 수 있지만 이런 식으로 하면 부호가 잘못되기가 매우 쉽습니다. 따라서 다항식의 뺄셈을 하려면 뺄셈 다항식(뺄셈 다항식)에 있는 모든 항의 부호를 변경한 다음 덧셈을 하는 것이 가장 좋습니다. 다항식을 빼는 것은 반대 다항식을 더하는 것과 같기 때문입니다.
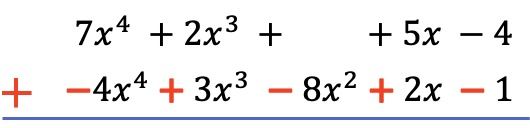
그리고 모든 항을 가장 높은 차수에서 가장 낮은 차수까지 순서대로 정렬하고 아래 다항식의 항을 부정한 후에 리터럴 부분을 동일하게 유지하면서 각 열의 계수를 추가합니다.
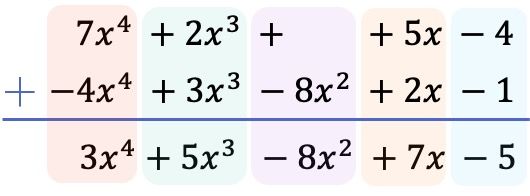
따라서 2개의 다항식을 빼서 얻은 결과는 다음과 같습니다.
![]()
마지막 단계가 명확하지 않은 경우, 다항식의 덧셈이 어떻게 수행되는지에 대한 설명을 남깁니다. 실제로 다항식을 성공적으로 뺄 수 있으려면 다항식의 덧셈을 마스터하는 것이 중요합니다. 링크된 페이지에서는 다항식 덧셈의 예와 해결 연습 문제도 찾을 수 있으며, 또한 다항식 덧셈과 뺄셈의 차이점도 볼 수 있습니다.
수평 다항식의 뺄셈
우리는 방금 다항식을 수직으로 뺄셈하는 방법을 살펴보았지만 이제 다항식을 뺄셈하는 또 다른 방법인 다항식을 수평으로 뺄셈하는 방법을 살펴보겠습니다. 이 과정은 확실히 이전 과정보다 빠르지만, 다항식의 개념에 대한 뛰어난 숙달이 필요합니다.
그러면 이 다항식을 뺄셈하는 방법이 무엇으로 구성되어 있는지 예를 통해 살펴보겠습니다. 두 방법의 차이점을 확인할 수 있도록 이전 예와 동일한 다항식을 뺍니다.
- 나머지 계산
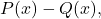
두 개의 다항식이 되는 것:
![]()
![]()
먼저 두 개의 다항식을 대수 연산의 형태로, 즉 차례로 놓아야 합니다.
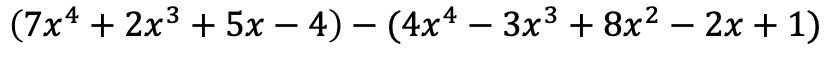
첫 번째 괄호의 단항식은 동일하게 유지되지만 두 번째 괄호의 항은 앞에 음수가 있으므로 부호를 변경해야 합니다.
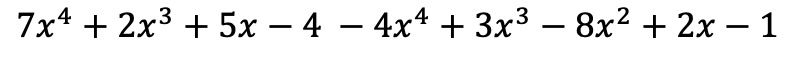
이제 문자 부분이 동일한 용어, 즉 변수(문자)와 지수가 동일한 용어를 그룹화합니다. 유사하지 않은 용어는 더하거나 뺄 수 없습니다.
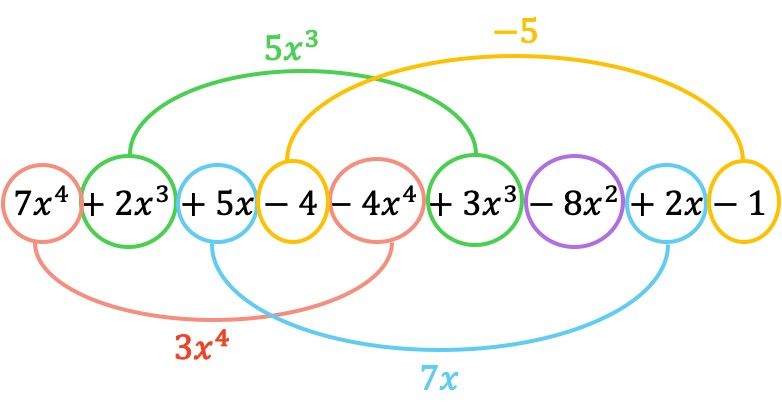
따라서 뺄셈으로 인한 다항식은 다음과 같습니다.
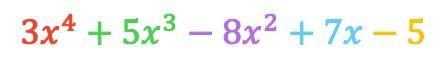
보시다시피 두 방법 모두에서 동일한 결과를 얻었으므로 가장 적합한 방법을 사용하면 됩니다.
이제 다항식 뺄셈을 푸는 두 가지 방법을 살펴보았 으므로 다항식을 사용하여 분수를 뺄 수도 있다는 것을 알고 계셨습니까? 뺄셈뿐만 아니라 모든 종류의 연산이 가능합니다. 이 링크를 클릭하여 대수 분수를 사용하여 연산을 수행하는 방법을 알아보세요.
다항식 빼기 문제 해결
연습할 수 있도록 몇 가지 다항식 뺄셈 문제를 해결해 보겠습니다. 운동에 관해 궁금한 점이 있으면 페이지 댓글로 문의하시면 최대한 빨리 답변해 드리겠습니다.
연습 1
다항식 빼기
![]()
다항식 빼기
![]()
![]()
![]()
이 경우 두 다항식을 수직으로 뺄 것입니다. 이를 위해 먼저 다항식을 차수별로 정렬한 다음 나머지 다항식 항의 부호를 변경하고 마지막으로 동일한 열에 있는 단항식을 추가합니다.
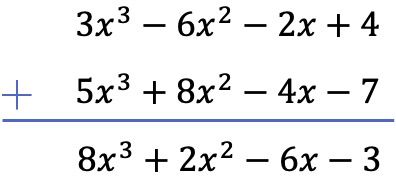
연습 2
뺄셈 다항식을 해결
![]()
다항식 빼기
![]()
![]()
![]()
두 다항식을 빼는 것은 뺄셈 다항식의 반대를 소다항식에 더하는 것과 같습니다. 따라서 하도급 다항식(나머지 하나)의 조건 부호를 변경하고 다항식을 추가합니다.
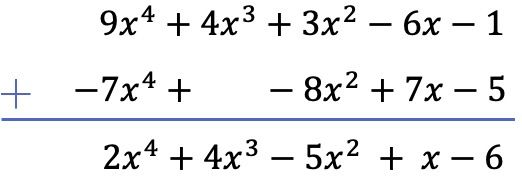
이 특별한 경우에는 두 번째 다항식의 3차 열에 3차 항이 없기 때문에 빈 공간이 남아 있어야 합니다.
연습 3
다항식을 뺀 결과 찾기
![]()
다항식 빼기
![]()
![]()
![]()
이 경우 두 다항식의 뺄셈을 수직으로 풀어보겠습니다. 따라서 먼저 다항식을 가장 큰 차수에서 가장 작은 차수까지 순서대로 놓은 다음 나머지 다항식 항의 부호를 변경하고 마지막으로 같은 항을 추가합니다.
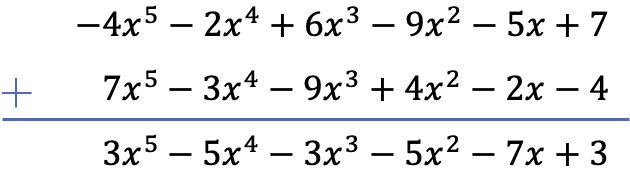
연습 4
다항식을 사용하여 다음 연산을 계산합니다.
![]()
![]()
![]()
![]()
이 경우 연산에는 3개의 다항식이 포함되며 그 중 2개는 뺄셈입니다. 따라서 연산을 풀기 위해 나머지 두 다항식의 모든 항의 부호를 변경한 다음 다항식을 추가하겠습니다.
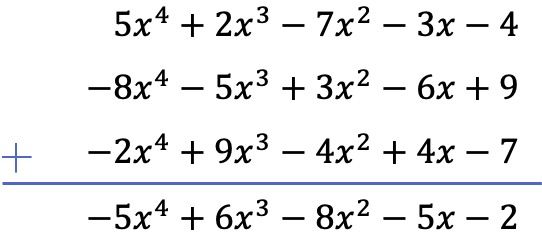
설명에 대해 어떻게 생각하시나요? 유용하다고 생각하셨나요? 다항식을 뺄 때 수직 또는 수평 중 어떤 방법을 선호합니까? 댓글에서 여러분의 의견을 읽었습니다! 🙌