루트에서 파생

여기에서는 근(또는 근호 함수)의 도함수를 취하는 방법을 설명합니다. 근을 나누는 공식과 근의 파생어에 대해 단계별로 풀어내는 연습문제를 찾을 수 있습니다.

근의 도함수에 대한 공식

근의 도함수 또는 무리함수는 근수의 도함수(근수 아래 표현)를 근의 지수 곱하기 동일한 근의 곱으로 나눈 후, 근의 지수에서 1을 뺀 것과 같습니다.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

그러나 근근수가 단지 x이면 공식이 단순화됩니다. 따라서 x의 근 도함수는 다음과 같습니다:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

간단히 말해서, 근을 도출하는 공식에는 두 가지가 있습니다. 첫 번째는 항상 사용할 수 있고 두 번째는 근호가 x일 때만 사용할 수 있습니다.

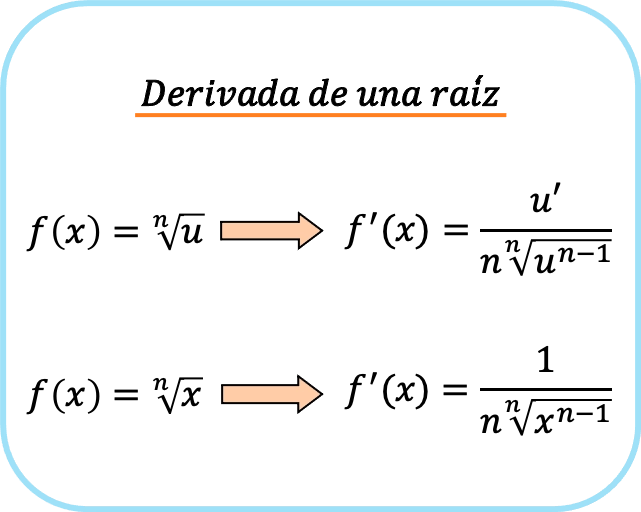
자세히 살펴보면 분수의 분자에 있는 항은 근의 도함수를 구할 때 연쇄 법칙을 적용한 결과입니다. 이것이 근수가 x일 때 x의 도함수이므로 분모에 1이 나타나는 이유입니다.

근 파생물의 예

근호 함수의 도함수에 대한 공식이 주어지면, 근의 도함수를 구하는 방법을 이해할 수 있도록 이러한 유형의 도함수에 대한 몇 가지 예를 아래에서 설명합니다.

예 1: 제곱근의 미분

그런 다음 제곱근의 미분이 무엇인지 살펴보겠습니다.

$f(x)=\sqrt{x}$

이 경우 루트 내부의 표현식은 단지 x이므로 다음 공식을 사용할 수 있습니다.

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

따라서 제곱근의 도함수는 1을 x의 제곱근에 2를 곱한 곱으로 나눈 것과 같습니다.

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

예 2: 세제곱근의 파생

$f(x)=\sqrt[3]{x}$

이 예에서 루트 아래의 표현식은 x이므로 다음 공식을 적용할 수 있습니다.

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

따라서 세제곱근의 도함수는 1을 x 제곱의 세제곱근에 3을 곱한 값으로 나눈 것과 같습니다.

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

예 3: 네 번째 근의 도함수

$f(x)=\sqrt[4]{7x-2}$

이제 근호 아래에 x가 없지만 더 복잡한 대수 표현이 있습니다. 따라서 근의 도함수에 대한 일반 공식을 사용해야 합니다.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

근호 아래의 표현식은 1차 함수이므로 그 도함수는 7입니다. 따라서 전체 함수의 도함수는 다음과 같습니다.

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

예 4: 한 뿌리에서 다른 뿌리로의 파생

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

다른 근으로 구성된 이 근의 도함수를 풀려면 다음 공식을 적용해야 합니다.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

이 경우 도함수를 계산하려면 동일한 수식을 두 번 연속 사용해야 합니다.

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

루트 파생 문제 해결

다음 근의 도함수를 계산합니다.

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

해결책 보기

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

루트에서 파생됨

근의 도함수에 대한 공식

근 파생물의 예

예 1: 제곱근의 미분

예 2: 세제곱근의 파생

예 3: 네 번째 근의 도함수

예 4: 한 뿌리에서 다른 뿌리로의 파생

루트 파생 문제 해결

댓글 달기 댓글 취소