공간에서 두 선 사이의 거리(r3)

이 페이지에서는 유형(평행선, 할선, 일치, 할선, 수직선 등)에 관계없이 공간에서 두 선 사이의 거리가 R3에서 어떻게 계산되는지 확인할 수 있습니다. 또한 단계별로 해결되는 예제와 연습문제도 볼 수 있습니다.

두 선 사이의 거리를 계산하는 방법

두 선 사이의 거리는 한 선의 모든 점과 다른 선의 모든 점 사이의 최소 거리입니다. 이 거리는 한 선에서 다른 선으로 이동하는 동시에 두 선에 수직인 세그먼트의 길이에 해당합니다.

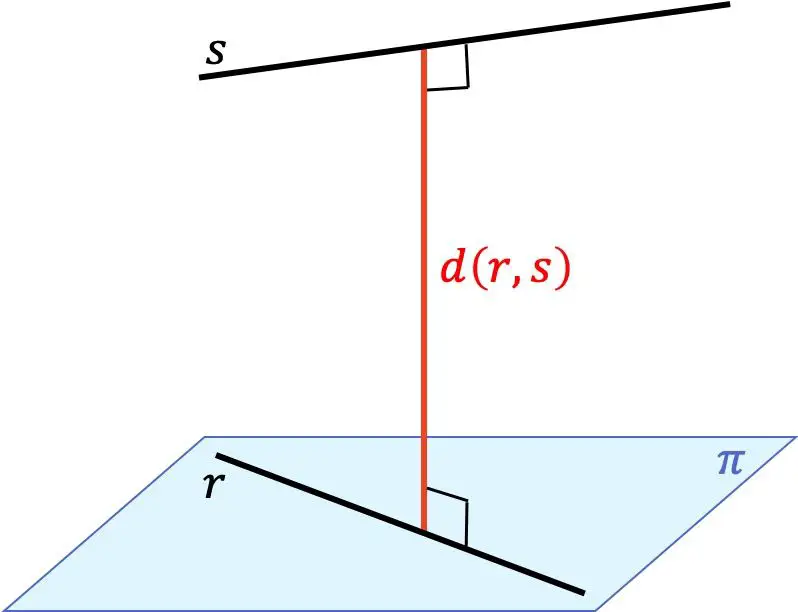
따라서 3차원(3D) 공간에서 서로 다른 두 선 사이의 거리를 찾는 것은 두 선 사이의 상대적인 위치에 따라 달라집니다.

• 두 선이 일치 하거나 교차하는 경우 두 선 사이의 거리는 (적어도) 한 지점에서 교차하기 때문에 0입니다.
• 두 선이 평행 할 때 선 중 하나의 점을 선택하고 해당 점과 다른 선 사이의 거리를 계산해야 합니다(아래에 이를 수행하는 방법에 대한 예가 있음).
• 두 선이 공간에서 교차하는 경우 교차하는 두 선 사이의 거리에 대한 공식을 적용해야 합니다(자세한 설명은 아래 참조).

따라서 두 선 사이의 거리를 계산하려면 먼저 선의 유형을 알아야 하며, 그런 다음 경우에 따라 하나 또는 다른 공식을 사용해야 합니다. 따라서 계속하기 전에 공간에서 두 선의 상대적 위치를 찾는 방법을 이미 익히는 것이 중요합니다. 그러나 링크에서 어떻게 수행되었는지 기억하지 못하는 경우 매우 완전한 설명과 예제 및 해결된 연습 문제를 볼 수 있습니다. 단계별로.

공간에서 두 평행선 사이의 거리를 찾는 방법

공간(R3)에서 두 평행선 사이의 거리를 계산하는 것은 평면(R2)에서와 동일한 방식으로 수행됩니다. 두 선 중 하나에서 점을 선택하고 다른 선에서 이 점의 거리를 찾아야 합니다. 선.

예를 들어, 공간에 있는 두 개의 평행선 사이의 거리 문제를 해결해 보겠습니다.

• 다음 두 평행선 사이의 거리는 얼마입니까?

두 선 모두 벡터 방정식의 형태로 표현되므로 방향 벡터와 각 선의 점을 쉽게 찾을 수 있습니다.

방향 벡터와 선의 점을 결정하는 방법에 대해 의문이 있는 경우 선의 방정식 에 대한 설명을 살펴보는 것이 좋습니다. 여기서는 선의 모든 방정식에 대해 설명했습니다. 선이 표현되는 방정식의 종류에 따라 방향 벡터와 선에 속하는 점을 찾는 것이 달라지기 때문입니다.

이제 두 평행선 사이의 거리를 찾으려면 점에서 선까지의 거리 공식을 적용해야 합니다.

그래서 한편으로 우리는 벡터 곱으로부터 생성된 벡터의 모듈을 계산합니다. 계산 방법에 대해 의문이 있는 경우 벡터 곱 공식을 참조할 수 있으며, 여기에서 벡터 간 이 연산의 예와 해결된 연습도 볼 수 있습니다.

그리고 다른 한편으로, 우리는 선의 벡터의 크기를 찾습니다.

마지막으로 각 항의 값을 공식에 대입하고 선 사이의 거리를 계산합니다.

따라서 두 선 사이의 거리는 3.60 단위입니다.

공간에서 교차하는 두 선 사이의 거리를 결정하는 방법

처음에 살펴본 것처럼 교차하는 두 선 사이의 거리를 결정하는 방법은 평행선 사이의 거리를 결정하는 절차와 다릅니다.

따라서 공간에서 교차하는 두 선 사이의 거리를 결정하는 방법에는 여러 가지가 있습니다. 이 페이지에서는 가장 간단한 절차 중 하나에 대해서만 설명합니다. 다른 두 가지 방법은 더 길고 복잡하기 때문에 실제로는 실제로 사용되지 않습니다.

두 개의 교차 선 사이의 거리를 결정하는 방법을 볼 수 있도록 예를 들어 문제를 해결하겠습니다.

• 다음 두 교차선 사이의 거리는 얼마입니까?

먼저 방향 벡터와 각 선의 점을 식별해야 합니다. 따라서 두 선은 연속 방정식의 형태로 표현됩니다.

이제 교차하는 두 선 사이의 거리에 대한 공식을 적용합니다.

한편으로는 혼합 곱(또는 삼중 스칼라 곱)을 해결합니다.

그리고 다른 한편으로는 교차곱(또는 교차곱) 모듈을 찾습니다.

마지막으로 교차된 두 선 사이의 거리를 공식의 각 항 값으로 대체합니다.