공간에서 두 선의 상대적 위치

여기서는 공간(R3)에서 두 선의 모든 상대적 위치를 찾을 수 있습니다. 또한 범위 또는 각 선의 점과 벡터라는 두 가지 가능한 방법을 사용하여 두 선 사이의 상대 위치를 찾는 방법을 설명합니다. 단계별로 해결되는 예제와 연습문제도 볼 수 있습니다.

공간에서 두 선의 상대적인 위치는 무엇입니까?

분석 기하학에서 3차원 공간(R3)에서 작업할 때 두 선 사이에는 4가지 상대 위치가 있을 수 있습니다. 두 선은 병합 선 , 평행선 , 할선 또는 할선 일 수 있습니다.

평행선

방향이 동일하지만 공통점이 없으면 두 선은 평행합니다. 또한 평행선은 항상 서로 같은 거리에 있습니다.

일치하는 선

두 선이 동일한 방향을 갖고 더구나 두 선의 모든 점이 공통이면 일치합니다.

교차선

교차하는 두 선은 방향이 다르지만 한 지점에서 만납니다.

교차선

교차하는 두 선은 방향이 다르며 어떤 지점에서도 교차하지 않습니다. 따라서 두 개의 교차된 선은 동일한 평면에 있지 않습니다. 예를 들어, 선 위의 그래픽 표현에서

$s$

항상 앞서 있다

$r$

, 그래서 그들은 결코 서로 접촉하지 않을 것입니다.

두 선 사이의 상대 위치를 알 수 있는 두 가지 방법이 있습니다. 두 선의 방정식이 표현되는 방식에 따라 달라지기 때문입니다.

선이 벡터, 파라메트릭 또는 연속 방정식 형식인 경우 점과 각 선의 벡터로부터 상대 위치를 계산하는 것이 가장 좋습니다(이 방법에 대한 설명은 아래에 제공됩니다).
반면, 암시적(또는 일반) 방정식의 형태로 선을 정의하면 두 행렬의 순위를 계산하여 두 선 사이의 상대적인 위치를 쉽게 알 수 있습니다 (아래 설명 참조).

점과 벡터에서 두 선의 상대적 위치 결정

각 선의 점과 벡터를 사용하여 두 선 사이에 어떤 상대 위치가 있는지 확인할 수 있습니다. 이 방법은 벡터방정식, 매개변수방정식, 연속방정식 등의 형태로 선을 정의할 때 사용하기에 적합하다.

따라서 방향 벡터와 두 선 각각의 점을 다음과 같이 설정합니다.

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

따라서 두 선의 상대적 위치를 찾으려면 다음 절차를 따라야 합니다.

▸ 가장 먼저 해야 할 일은 두 선의 벡터가 비례하는지 여부를 확인하는 것이며, 경우에 따라 다음을 수행합니다.

두 벡터가 비례하는 경우 선은 평행하거나 일치할 수 있습니다. 따라서 한 선의 점이 다른 선의 방정식을 만족하는지 확인해야 합니다.
- 한 선의 점이 다른 선의 방정식을 만족하면 두 선이 일치한다는 의미입니다.
- 그렇지 않으면 두 선이 평행하다는 것을 의미합니다.
두 벡터가 비례하지 않으면 선이 교차하거나 교차할 수 있습니다. 이 경우 다음과 같은 3×3 행렬식을 풀어야 합니다.

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- 이전 행렬식이 0이면 두 선은 한 점에서 교차합니다(교차합니다).
- 이전 행렬식이 0과 다르면 두 선이 교차합니다.

다음 그래픽은 전체 절차를 요약합니다.

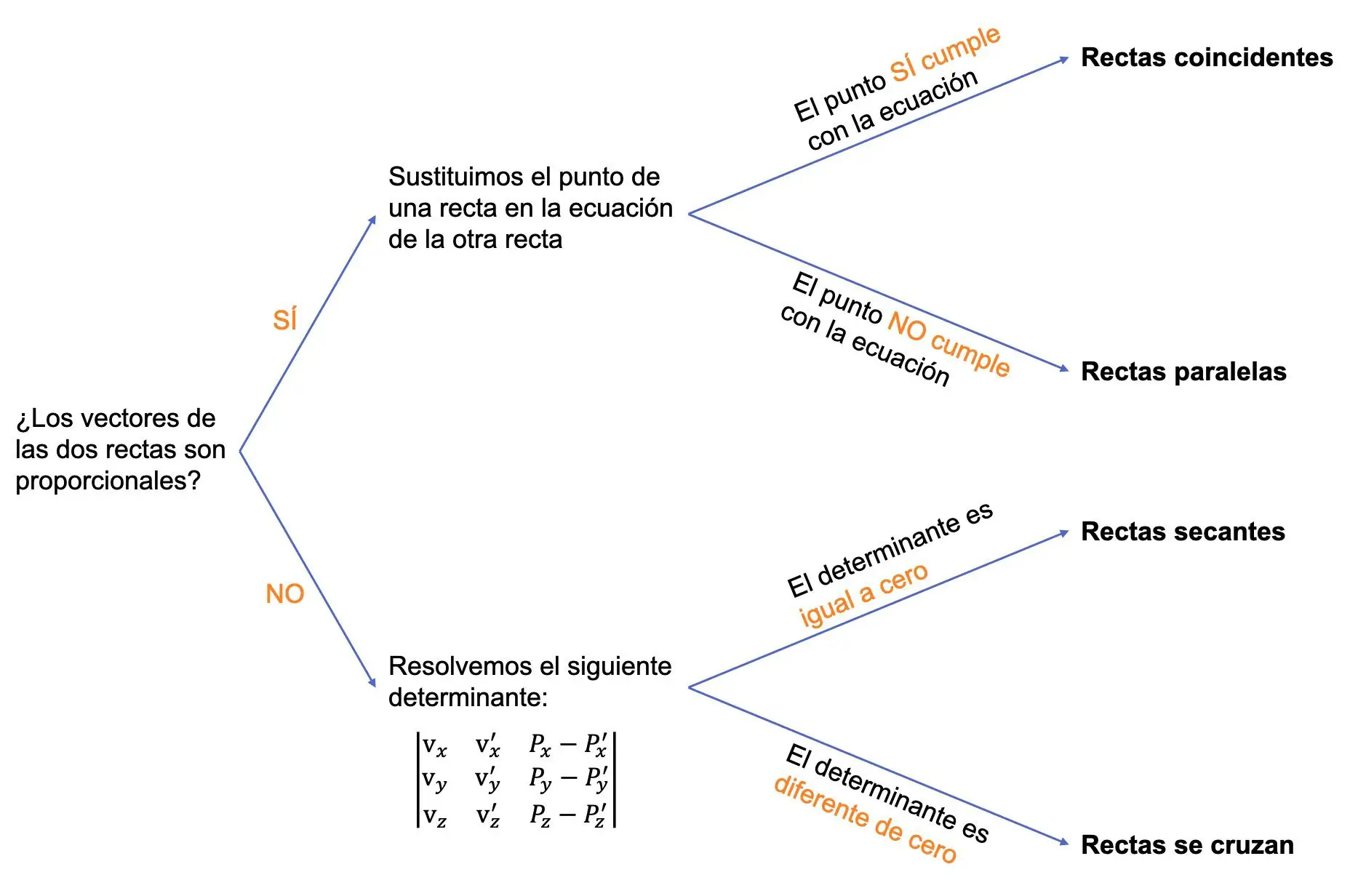
두 선 사이의 상대 위치를 결정하는 예

이전 절차는 다소 복잡해 보일 수 있지만 반대임을 알 수 있도록 예를 들어 문제를 해결하겠습니다.

다음 두 줄 사이의 상대 위치를 결정합니다.

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

두 선은 벡터 방정식으로 표현되며, 각 선의 방향 벡터는 다음과 같습니다.

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

그리고 각 선이 통과하는 지점은 다음과 같습니다.

$R(2,0,1)\qquad \qquad S(1,-3,1)$

점과 각 선의 방향 벡터를 알고 나면 위에서 본 방법을 적용합니다. 우선 벡터의 좌표가 비례하는지 확인해야 합니다.

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

두 벡터는 서로 비례하지 않으므로 선은 서로 닿거나 교차할 수만 있습니다. 따라서 이제 방향 벡터와 각 선의 점으로 구성된 다음 행렬식을 풀어야 합니다.

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

값을 공식으로 대체합니다.

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

그리고 우리는 행렬식을 계산합니다. 이를 위해 모든 방법(Sarrus 규칙, 보완 방법 또는 보조 인자 방법 등)을 사용할 수 있습니다.

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

판정 결과가 0인 경우 이는 선이 교차(접촉)한다는 의미입니다. 그러나 행렬식이 0과 다르므로 선이 교차합니다 .

행별로 두 줄의 상대 위치 찾기

두 행의 상대적 위치를 찾는 또 다른 방법은 다음에 살펴보겠지만 두 구체적인 행렬의 순위를 계산하는 것입니다. 이 방법은 두 직선이 암시적(또는 일반) 방정식 형식일 때 매우 유용합니다.

따라서 3차원 공간(R3)에서 암시적(또는 일반) 방정식으로 표현된 두 개의 선이 있는 경우:

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

A를 두 선의 계수로 구성된 행렬로 설정합니다.

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

그리고 두 직선의 모든 매개변수로 구성된 행렬인 확장 행렬 A’가 주어지면:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

그런 다음 두 행의 상대적 위치는 다음 표에 따라 이전 두 행렬의 범위에 의해 결정될 수 있습니다.

따라서 두 행 사이의 상대 위치를 찾으려면 두 행렬의 순위를 계산해야 하며 각 행렬의 순위에 따라 두 가지 경우가 됩니다.

이 정리는 Rouché-Frobenius 정리(선형 방정식 시스템을 해결하는 데 사용되는 방법)를 사용하여 증명할 수 있지만, 이 정리는 매우 번거롭고 많은 것을 추가하지 않기 때문에 증명을 수행하지 않습니다.

범위별로 두 선의 상대 위치를 찾는 방법의 예

두 줄 사이의 상대적 위치에 대한 이론을 행 단위로 살펴본 후 예제를 통해 실제로 어떻게 적용되는지 살펴보겠습니다.

다음 두 줄의 상대적 위치를 찾으세요.

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

두 선은 일반(또는 암시적) 방정식의 형태이므로 순위 방법을 사용하여 두 선 사이의 상대적 위치를 찾습니다. 따라서 우리는 선의 계수를 사용하여 행렬 A와 확장 행렬 A’를 구성합니다.

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

두 행렬이 모두 있으면 각 행렬의 순위를 계산해야 합니다. 먼저 행렬식에 따라 행렬 A의 순위를 계산합니다.

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

행렬 A는 0이 아닌 3×3 부분행렬의 행렬식을 포함하므로 행렬 A의 순위는 3입니다 .

이제 확장 행렬 A’의 범위를 계산합니다. 행렬 A’는 항상 적어도 행렬 A의 순위에 있을 것입니다. 이 경우 행렬 A의 순위는 3이므로 순위 4인지 순위 3인지 확인하는 것으로 충분합니다. 이를 위해 우리는 행렬식을 해결합니다. 덧셈(또는 보조인자)에 의한 4× 행렬 4:

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

전체 확장 행렬의 행렬식은 0이므로 행렬 A’도 랭크 3입니다 .

따라서 행렬 A와 행렬 A’는 랭크 3이므로 결과적으로 두 선이 교차합니다 . 즉, 둘 사이의 교차점은 단 하나뿐입니다.

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

행렬 A와 A’의 범위에 따라 두 선 사이의 가능한 모든 상대 위치 사례를 요약한 표가 위에 있다는 것을 기억하십시오.

공간에서 두 선 사이의 상대적 위치 문제 해결

연습 1

다음 두 줄 사이의 상대 위치를 찾으세요.

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

해결책 보기

두 선 모두 벡터 방정식으로 표현되므로 각 선의 한 점과 한 벡터 방법으로 두 선 사이의 상대적인 위치를 구해보겠습니다.

각 선의 방향 벡터는 다음과 같습니다.

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

그리고 각 선에 속하는 점은 다음과 같습니다.

$R(3,4,0)\qquad \qquad S(1,-2,2)$

따라서 이 절차를 적용하려면 먼저 방향 벡터의 구성 요소가 비례하는지 확인해야 합니다.

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

두 벡터는 서로 비례하지 않으므로 선은 교차하거나 교차할 수만 있습니다. 따라서 이제 방향 벡터와 각 선의 점으로 구성된 다음 행렬식을 풀어야 합니다.

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

값을 공식으로 대체합니다.

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

그리고 우리는 행렬식을 계산합니다:

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

결정자의 결과는 0과 동일하므로 선이 교차합니다 .

연습 2

다음 두 줄의 상대 위치를 계산합니다.

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

해결책 보기

첫 번째 선은 매개변수 방정식의 형태이고 두 번째 선은 연속 방정식의 형태로, 이를 통해 각 선의 1점 벡터 방법을 통해 두 선 사이의 상대 위치를 결정하게 됩니다.

오른쪽 방향 벡터의 좌표

$r$

매개변수 앞의 계수는 다음과 같습니다.

$t,$

그리고 선의 방향 벡터의 좌표

$s$

분모의 숫자는 다음과 같습니다.

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

그리고 각 선에 속하는 점은 다음과 같습니다.

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

따라서 이 절차를 적용하려면 먼저 방향 벡터의 구성 요소가 비례하는지 확인해야 합니다.

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

두 벡터는 서로 비례하므로 선은 평행하거나 일치할 수만 있습니다. 이 의심을 제거하려면 선의 점을 대체해야 합니다.

$r$

직선의 방정식에서

$s$

(또는 그 반대로) 상기 방정식을 만족하는지 확인하려면 다음을 수행하십시오.

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

선의 점을 대체함으로써 우리는 동일성을 얻습니다. 따라서 한 선의 점이 다른 선의 방정식을 충족하고 더욱이 방향 벡터가 비례합니다. 따라서 두 선이 일치합니다.

연습 3

다음 두 줄의 상대적 위치를 찾으세요.

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

해결책 보기

두 선은 일반(또는 암시적) 방정식 형식이므로 순위 방법을 사용하여 두 선 사이의 상대적 위치를 찾습니다. 따라서 우리는 선의 계수를 사용하여 행렬 A와 확장된 행렬 A’를 만듭니다.

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

두 행렬이 모두 있으면 각 행렬의 순위를 계산해야 합니다. 먼저 행렬식에 따라 행렬 A의 순위를 계산합니다.

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

행렬 A의 모든 3×3 행렬식은 0이지만 행렬 내부에는 0이 아닌 2×2 행렬식이 있으므로 행렬 A의 순위는 2 입니다 .

이제 확장 행렬 A’의 범위를 계산합니다. 행렬 A’는 항상 적어도 행렬 A의 범위(이 경우 2)가 됩니다. 따라서 취소되지 않는 3×3 행렬식이 있는지 확인하고 행렬식의 행렬식은 얼마인지 확인해야 합니다. 전체 매트릭스:

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

확장된 행렬 A’는 실제로 0이 아닌 3×3 하위 행렬식을 포함하며, 게다가 전체 확장 행렬의 행렬식은 0과 동일하므로 행렬 A’의 순위는 3입니다 .

따라서 행렬 A는 랭크 2이고 행렬 A’는 랭크 3이므로 두 선은 평행합니다 . 즉, 공통점이 하나도 없습니다.

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

위의 방법에 대한 설명에는 행렬 A와 A’의 순위에 따라 두 선 사이의 가능한 모든 상대 위치 사례를 요약하는 표가 있다는 것을 기억하십시오.

연습 4

다음 두 줄의 상대적 위치를 찾으세요.

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

해결책 보기

이 경우 두 선은 데카르트(또는 암시적) 방정식 형식이므로 순서 지정 방법을 사용하여 두 선 사이의 상대적 위치를 찾습니다. 따라서 우리는 선의 계수를 사용하여 행렬 A와 확장 행렬 A’를 구성합니다.

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

두 행렬을 알고 나면 각각의 순위를 계산해야 합니다. 먼저 행렬식에 따라 행렬 A의 순위를 계산합니다.

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

행렬 A에는 행렬식이 0이 아닌 3×3 부분 행렬이 포함되어 있으므로 행렬 A의 순위는 3입니다 .

이제 확장 행렬 A’의 범위를 계산합니다. 행렬 A’는 항상 최소한 행렬 A의 순위에 속하며 이 경우에는 3의 가치가 있으므로 순위 4인지 순위 3인지 확인하는 것으로 충분합니다. 이를 위해 다음의 행렬식을 해결합니다. 덧셈(또는 보조 인자)에 의한 4×4 행렬 세트:

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$