곱의 파생(또는 곱셈)

이 글에서는 두 함수(공식)의 곱을 도출하는 방법을 설명합니다. 또한, 함수곱의 도함수에 대한 몇 가지 예를 볼 수 있으며 곱셈 도함수에 대한 연습 문제도 연습할 수 있습니다.

제품 파생 공식

두 개의 서로 다른 함수의 곱의 도함수는 두 번째 미분 함수에 의한 첫 번째 함수의 도함수와 두 번째 함수의 도함수에 의한 첫 번째 미분 함수의 곱의 곱과 같습니다.

즉, f(x) 와 g(x) 가 서로 다른 두 함수인 경우 두 함수 간의 곱셈의 도함수 공식은 다음과 같습니다.

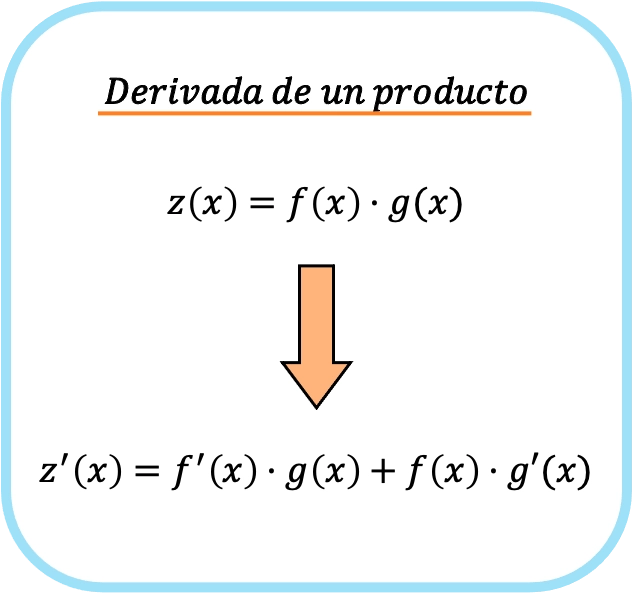
따라서 곱의 도함수 규칙을 적용하여 단순한 곱셈에서 두 개의 서로 다른 곱으로 이동합니다.

제품 파생물의 예

곱셈(또는 곱셈)의 도함수 공식이 무엇인지 알게 되면 이러한 유형의 도함수에 대한 몇 가지 예를 풀 것입니다. 이렇게 하면 두 함수의 곱이 어떻게 파생되는지 이해하기가 훨씬 쉬워집니다.

실시예 1

이 예에서는 다음을 곱하여 두 가지 잠재적 함수의 미분을 해결합니다.

이전 섹션에서 살펴본 것처럼 곱셈의 미분 공식은 다음과 같습니다.

따라서 먼저 각 함수의 도함수를 개별적으로 계산해야 합니다.

그리고 각 함수의 도함수를 알면 두 함수의 곱의 도함수에 대한 공식을 적용할 수 있습니다. 즉, 첫 번째 요소의 도함수에 미분하지 않고 두 번째 요소를 곱한 다음 두 번째 요소의 도함수로 미분하지 않고 첫 번째 요소의 곱을 더합니다.

마지막으로 얻은 결과를 단순화하기 위한 작업을 수행합니다.

실시예 2

이 경우 우리는 함수에 의해 상수의 곱을 유도할 것입니다:

제품의 미분 규칙은 다음과 같습니다.

따라서 우리는 제품의 일부인 각 기능을 별도로 파생합니다.

그런 다음 곱셈의 도함수에 대한 규칙을 적용합니다.

상수의 미분은 항상 0이므로 상수에 함수를 곱한 미분은 상수와 함수의 미분의 곱과 같다고 추론할 수 있습니다.

실시예 3

지수함수와 자연로그 사이의 곱을 풀어보겠습니다.

두 함수의 곱셈의 미분 공식은 다음과 같습니다.

따라서 먼저 곱을 구성하는 각 함수의 도함수를 별도로 만들어야 하며, 이는 다음과 같습니다.

따라서 함수의 파생 제품은 다음과 같습니다.

제품 파생물에 대한 해결 연습

다음과 같은 기능 제품을 파생합니다.

3가지 기능을 갖춘 제품에서 파생됨

다음으로, 3개 함수의 곱셈의 미분 공식을 알려드리겠습니다. 이는 2개 함수의 공식과 매우 유사하고 경우에 따라 유용할 수 있기 때문입니다.

세 함수의 곱의 도함수는 첫 번째 함수와 다른 두 함수의 도함수, 두 번째 함수와 다른 두 함수의 도함수의 곱, 그리고 다음 함수의 도함수의 곱과 같습니다. 세 번째 function.function은 다른 두 함수에 의해 수행됩니다.

예를 들어, 세 가지 다른 함수의 다음과 같은 곱셈을 도출하려는 경우:

도함수를 풀려면 세 함수의 곱의 도함수 규칙을 적용해야 합니다. 따라서:

제품 파생물에 대한 공식 시연

마지막으로 곱셈의 미분 공식을 보여드리겠습니다. 외울 필요는 없지만 공식이 어디에서 왔는지 이해하는 것이 항상 좋습니다. 🙂

미분의 수학적 정의에서:

함수 z를 두 가지 다른 함수의 곱으로 둡니다.

그러면 정의에 따라 z 의 미분은 다음과 같습니다.

우리가 알고 있듯이 항을 덧셈과 뺄셈으로 더하면 둘 다 같은 항이면 결과에 영향을 주지 않습니다. 따라서 다음 단계로 넘어갈 수 있습니다.

이제 경계 속성을 사용하여 이전 경계를 두 개의 서로 다른 경계로 분리합니다.

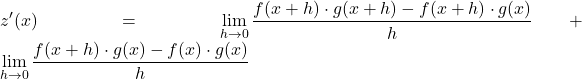
두 분수의 분자에서 공통 인수를 추출합니다.

반면에 우리는 다음 극한의 결과를 알고 있습니다.

따라서 제한을 단순화할 수 있습니다.

마지막으로 나머지 두 극한을 살펴보면 각각은 함수의 도함수의 정의에 해당합니다. 따라서 평등은 다음과 같이 단순화될 수 있습니다.

또는 이에 상응하는 것: