이 페이지에서는 2×2 행렬의 행렬식이 무엇인지 배우게 됩니다. 또한 2차 행렬식을 푸는 방법에 대한 단계별 풀이 예시와 연습문제도 함께 제공되므로 완벽하게 연습하고 이해할 수 있습니다.
2×2 행렬식이란 무엇입니까?
2차 행렬식은 행렬의 양쪽에 세로 막대로 표시되는 2×2 차원의 행렬입니다. 예를 들어 다음과 같은 행렬이 있다고 가정해 보겠습니다.
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50ff006696d04e4eee005e245ba217e4_l3.png)
행렬 A의 행렬식은 다음과 같이 표현됩니다.
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dc95ca8f173419691852fd137d67154_l3.png)
보시다시피 2×2 정사각 행렬의 행렬식을 작성하는 것은 쉽습니다. 이제 계산 방법을 살펴보겠습니다.
2차 행렬식을 어떻게 푸나요?
2×2 행렬의 행렬식을 계산 하려면 주대각선의 요소를 곱하고 보조대각선의 곱을 빼야 합니다.
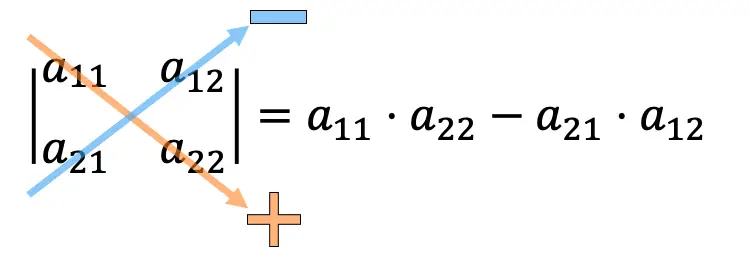
2×2 행렬식 계산의 예:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-228cbdabc4e6d330b56fae20f5163e64_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e9aed81d00e74873a5e797746861a51_l3.png)
2 × 2 행렬의 행렬식 문제 해결
연습 1
다음 2×2 행렬식을 계산합니다.
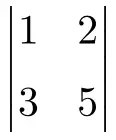
2×2 행렬식을 만들려면 주대각선의 요소를 곱하고 보조 대각선의 곱을 빼야 합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d03764083647c0b05f9a5d7266c8915_l3.png)
연습 2
차원 2×2의 다음 행렬식을 풉니다.
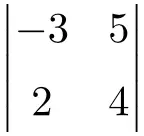
2차 행렬식의 해를 찾으려면 주대각선의 요소를 곱하고 보조 대각선의 곱을 빼야 합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56c917d70b8c6ec3697612d44f84e522_l3.png)
연습 3
다음 차수 2의 행렬식에 대한 해를 구합니다.
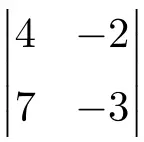
차원 2의 행렬식에 대한 해를 찾으려면 주대각선의 요소를 곱하고 보조 대각선의 곱을 빼야 합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cbd06fd83283d3e82105c24eaf95af9f_l3.png)
연습 4
다음 2×2 행렬식을 계산합니다.
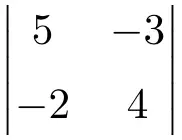
2×2 행렬의 행렬식을 계산하려면 주대각선의 요소를 곱하고 보조대각선의 곱을 빼야 합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}](https://mathority.org/wp-content/ql-cache/quicklatex.com-34915d9aff298587a13346c6fc30bfcd_l3.png)
연습 5
다음 2×2 행렬식의 결과를 결정합니다.
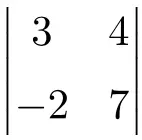
2×2 행렬식의 해를 찾으려면 주대각선의 요소를 곱하고 두 번째 대각선의 곱을 빼야 합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c6e4a7fdc04f0458d95c1d62b12d7ac_l3.png)
밝은! 이제 2×2 차원의 행렬식을 만드는 방법을 알았습니다! 이제 여러분은 3×3 행렬식이 어떻게 계산되는지, 그리고 4×4 행렬의 행렬식이 어떻게 해결되는지 이미 이해할 수 있을 것입니다.