평면의 매개변수 방정식

이 페이지에서는 계획의 매개변수 방정식이 무엇인지, 어떻게 계산되는지(공식)를 확인할 수 있습니다. 또한 단계별로 예제를 보고 연습문제를 풀어볼 수 있습니다.

평면의 매개변수 방정식은 무엇입니까?

분석 기하학에서 평면의 매개변수 방정식은 모든 평면을 수학적으로 표현할 수 있는 방정식입니다. 평면의 매개변수 방정식을 찾으려면 점과 해당 평면에 속하는 두 개의 선형 독립 벡터만 필요합니다.

계획의 매개변수 방정식 공식화

평면의 점과 두 방향 벡터를 고려하십시오.

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

평면의 매개변수 방정식에 대한 공식은 다음과 같습니다.

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

금

$\lambda$

그리고

$\mu$

는 두 개의 스칼라, 즉 두 개의 실수를 의미합니다.

평면 방정식의 두 방향 벡터가 선형적으로 독립적이라는 것, 즉 서로 다른(비평행) 방향을 갖는 것이 중요합니다. 그렇지 않으면 위의 방정식은 계획이 없음을 나타냅니다.

한편, 파라메트릭 방정식 외에도 일반 평면 방정식 과 같이 공간(R3)에서 평면을 분석적으로 표현하는 다른 방법이 있다는 점을 명심하세요. 이 링크에서는 공식, 계획의 매개변수 방정식, 예제 및 해결된 연습에서 계산되는 방법을 찾을 수 있습니다.

평면의 매개변수 방정식을 찾는 방법의 예

평면의 매개변수 방정식이 무엇인지 확인한 후에는 예를 사용하여 이것이 어떻게 계산되는지 살펴보겠습니다.

점을 통과하는 평면의 매개변수 방정식을 구합니다.
$P(1,3,2)$

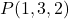
그리고 벡터를 포함합니다

$\vv{\text{u}}=(2,0,-1)$

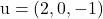
그리고

$\vv{\text{v}}=(4,2,3)$

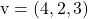
계획의 매개변수 방정식을 결정하려면 해당 공식을 적용하면 됩니다.

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

이제 점과 각 방향 벡터를 방정식으로 대체합니다.

$\displaystyle \begin{cases}x=1 + \lambda \cdot 2 + \mu \cdot 4 \\[1.7ex] y=3+ \lambda \cdot 0 + \mu \cdot 2\\[1.7ex] z=2 + \lambda\cdot (-1)+ \mu \cdot 3\end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + 2\lambda + 4\mu } \\[1.7ex] \bm{y=3 + 2\mu}\\[1.7ex] \bm{z=2 -\lambda+ 3\mu} \end{cases}$

평면의 벡터 방정식에서 파라메트릭 방정식으로 이동하는 방법

평면의 매개변수 방정식을 결정하는 또 다른 방법은 평면의 벡터 방정식을 이용하는 것입니다. 아래에서 데모를 볼 수 있습니다.

모든 평면의 벡터 방정식은 다음과 같습니다.

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

우리는 스칼라에 의한 벡터의 곱을 연산하고 먼저 수행합니다.

$(x,y,z)=(P_x,P_y,P_z)+ (\lambda\text{u}_x,\lambda\text{u}_y,\lambda\text{u}_z) +(\mu\text{v}_x,\mu\text{v}_y,\mu\text{v}_z)$

다음으로 구성 요소를 추가합니다.

$(x,y,z)=(P_x+\lambda \text{u}_x + \mu \text{v}_x,P_y+\lambda \text{u}_y + \mu \text{v}_y,P_z+\lambda \text{u}_z + \mu \text{v}_z)$

그리고 마지막으로 각 변수에 해당하는 좌표를 개별적으로 동화하여 평면의 매개변수 방정식을 얻습니다.

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

위의 두 예에서 볼 수 있듯이 평면의 매개변수 방정식을 찾는 것은 비교적 쉽습니다. 그러나 문제가 약간 복잡해질 수 있으므로 아래에는 연습할 수 있도록 다양한 난이도의 몇 가지 해결된 연습 문제가 있습니다.

평면의 매개변수 방정식 문제 해결

연습 1

벡터가 포함된 평면의 매개변수 방정식을 결정합니다.

$\vv{\text{u}}=(2,1,5)$

다음 두 가지 사항을 살펴봅니다.

$A(3,2,-1)$

그리고

$B(-2,-1,1).$

해결책 보기

평면의 방정식을 알려면 점 하나와 벡터 두 개가 필요합니다. 이 경우 벡터는 하나뿐이므로 평면의 또 다른 방향 벡터를 찾아야 합니다. 이를 위해 평면의 두 점을 정의하는 벡터를 계산할 수 있습니다.

$\vv{AB} = B - A = (-2,-1,1) - (3,2,-1) = (-5,-3,2)$

이제 우리는 평면과 점의 두 방향 벡터를 이미 알고 있으므로 평면의 매개변수 방정식에 대한 공식을 사용합니다.

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

그리고 두 벡터와 평면의 두 점 중 하나를 방정식으로 대체합니다.

$\displaystyle \begin{cases}x=3 + \lambda \cdot 2+ \mu \cdot (-5) \\[1.7ex] y=2 + \lambda \cdot 1 + \mu \cdot (-3) \\[1.7ex] z=(-1) + \lambda\cdot 5 + \mu \cdot 2 \end{cases}$

$\displaystyle \begin{cases}\bm{x=3 +2 \lambda-5\mu } \\[1.7ex] \bm{y=2 + \lambda-3 \mu } \\[1.7ex] \bm{z=-1 + 5\lambda + 2\mu } \end{cases}$

연습 2

다음 세 점을 포함하는 평면의 매개변수 방정식을 구합니다.

$A(4,1,0) \qquad B(2,-3,-1) \qquad C(1,5,3)$

해결책 보기

평면의 매개변수 방정식을 찾으려면 평면에서 연결되는 두 개의 선형 독립 벡터를 찾아야 합니다. 그리고 이를 위해 3개의 점으로 정의되는 두 개의 벡터를 계산할 수 있습니다.

$\vv{AB} = B - A = (2,-3,-1) - (4,1,0) = (-2,-4,-1)$

$\vv{AC} = C - A = (1,5,3) - (4,1,0) = (-3,4,3)$

발견된 두 벡터의 좌표는 비례하지 않으므로 서로 선형 독립입니다.

이제 우리는 이미 두 개의 방향 벡터와 평면의 한 점을 알고 있으므로 평면의 매개변수 방정식에 대한 공식을 적용합니다.

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

그리고 두 벡터와 평면의 세 점 중 하나를 방정식에 대체합니다.

$\displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}$

$\displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}$

연습 3

다음 벡터 방정식으로 정의된 평면의 매개변수 방정식을 계산합니다.

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

해결책 보기

평면의 벡터 방정식을 파라메트릭 방정식으로 변환하려면 좌표를 사용하여 작업한 다음 각 변수를 별도로 풀어야 합니다.

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

$(x,y,z)=(0,-1,5)+(6\lambda,\lambda,-2\lambda) + (\mu,-\mu,3\mu)$

$(x,y,z)=(6\lambda+\mu,-1+\lambda-\mu,5-2\lambda+3\mu)$

$\displaystyle \begin{cases}\bm{x=6\lambda+\mu } \\[1.7ex] \bm{y=-1+\lambda-\mu} \\[1.7ex] \bm{z=5-2\lambda+3\mu } \end{cases}$

연습 4

선을 포함하는 평면의 매개변수 방정식을 찾습니다.

$r$

그리고 오른쪽과 평행하다

$s.$

라인 :

$\displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}$

해결책 보기

평면의 매개변수 방정식을 찾으려면 두 개의 방향 벡터와 평면 위의 한 점을 알아야 합니다. 명령어는 다음 줄이 포함되어 있음을 알려줍니다.

$r$

따라서 방향 벡터와 이 선의 점을 사용하여 평면을 정의할 수 있습니다. 게다가 이 진술은 평면이 선과 평행하다는 것을 알려줍니다.

$s,$

따라서 평면 방정식에 이 선의 방향 벡터를 사용할 수도 있습니다.

권리

$r$

매개변수 방정식의 형태로 표현되므로 방향 벡터의 구성요소는 매개변수 항의 계수입니다.

$t:$

$\vv{r} =(1,-3,2)$

그리고 같은 선에 있는 점의 데카르트 좌표는 매개변수 방정식의 독립 항입니다.

$P(1,2,4)$

반면 직선은

$s$

방향 벡터의 구성 요소가 분수의 분모가 되는 연속 방정식의 형태입니다.

$\vv{s} =(2,2,-3)$

따라서 계획의 매개변수 방정식은 다음과 같습니다.

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

$\displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}$

평면의 매개변수 방정식은 무엇입니까?

계획의 매개변수 방정식 공식화

평면의 매개변수 방정식을 찾는 방법의 예

평면의 벡터 방정식에서 파라메트릭 방정식으로 이동하는 방법

평면의 매개변수 방정식 문제 해결

연습 1

연습 2

연습 3

연습 4

댓글 달기 댓글 취소