타원 방정식

여기에서는 원점이 중심인지 여부에 관계없이 타원 방정식(공식)이 계산되는 방법을 확인할 수 있습니다. 또한 타원의 요소가 무엇인지, 어떻게 계산하는지, 어떤 용도로 사용되는지 알아볼 수 있습니다. 또한 타원 방정식의 예와 해결 연습을 볼 수 있습니다.

타원 방정식 공식

데카르트 좌표의 타원 방정식 공식은 다음과 같습니다.

$\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1$

금:

$x_0$

그리고

$y_0$

타원 중심의 좌표는 다음과 같습니다.

$C(x_0,y_0)$
$a$

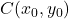
타원의 수평 반경입니다.
$b$

타원의 수직 반경입니다.

원점을 중심으로 하는 타원의 방정식

매우 일반적인 유형의 타원은 중심이 좌표의 원점, 즉 점 (0,0)에 있는 타원입니다. 이것이 우리가 원점을 중심으로 하는 타원의 방정식을 구하는 방법을 알아보는 이유입니다.

타원 방정식의 공식은 다음과 같습니다.

$\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1$

타원이 좌표 원점의 중심에 있으면 이는 다음을 의미합니다.

$x_0$

그리고

$y_0$

는 0과 같으므로 방정식은 다음과 같습니다.

$\cfrac{\bm{x^2}}{\bm{a^2}}+\cfrac{\bm{y^2}}{\bm{b^2}} \bm{= 1}$

이 표현을 표준 방정식 또는 타원의 축소 방정식이라고 부르는 수학자도 있습니다.

타원의 요소

타원의 방정식이 어떻게 생겼는지 확인한 후에는 그 요소가 무엇인지 살펴보겠습니다. 하지만 먼저 타원이 정확히 무엇인지 기억해 봅시다.

타원은 원주와 매우 유사한 평평하고 닫힌 곡선이지만 모양은 더 타원형입니다. 특히 타원은 다른 두 고정점(초점 F 및 F’라고 함)까지의 거리의 합이 일정한 평면의 모든 점의 자취입니다.

따라서 타원의 요소는 다음과 같습니다.

초점 : 고정점 F와 F'(아래 이미지에서 보라색 점)입니다. 타원의 한 점과 각 초점 사이의 거리의 합은 타원의 모든 점에 대해 일정합니다.
주축 또는 초점축 : 초점이 위치한 타원의 대칭축입니다. 장축이라고도 합니다.
보조축(Secondary axis) : 주축에 수직인 타원의 대칭축입니다. 단축이라고도 하며 초점을 연결하는 세그먼트의 수직 이등분선에 해당합니다.
중심 : 타원 축의 교차점입니다. 또한 타원의 대칭 중심(그래프의 주황색 점)입니다.
정점 : 타원과 대칭축(검은색 점)이 교차하는 지점입니다.
장반경축 또는 주축: 타원의 중심에서 주축의 꼭지점까지 가는 선분.
반단축 또는 보조 축: 타원의 중심과 보조 축의 정점 사이의 세그먼트입니다.
초점 거리 : 두 초점 사이의 거리입니다.
반초점거리 : 중심과 각 초점 사이의 거리에 해당합니다.
라디오 벡터 : 타원의 임의 지점을 각 초점에 연결하는 세그먼트입니다(그래프의 파란색 세그먼트).

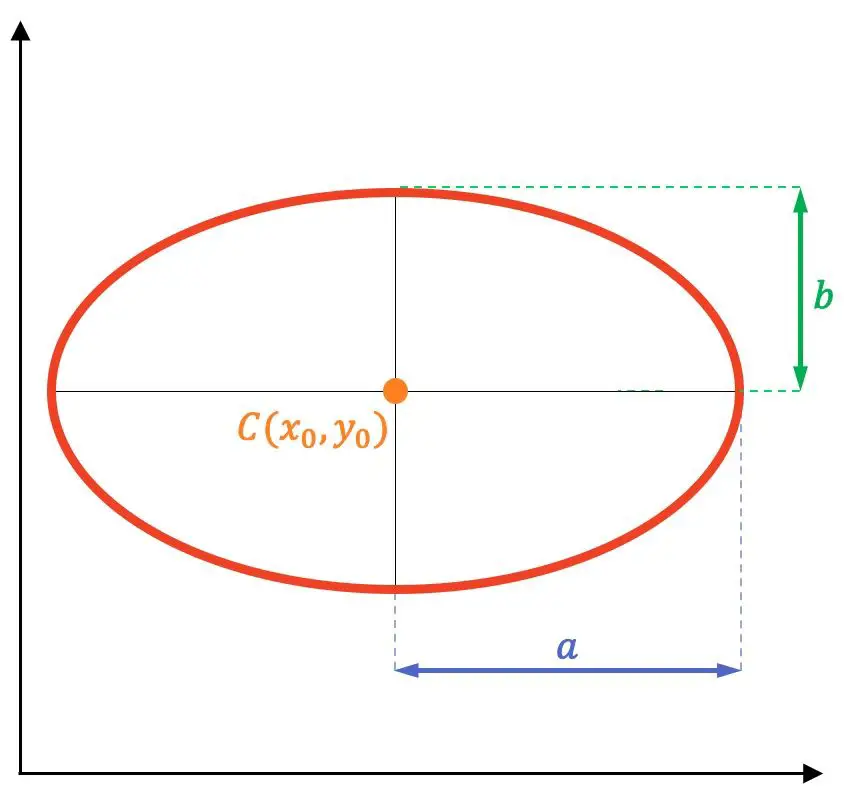
타원 요소 간의 관계

타원의 다양한 요소는 서로 연결되어 있습니다. 또한 이들 사이의 관계는 일반적으로 타원 문제를 해결하고 방정식을 결정하는 데 필요하기 때문에 타원 연습에 매우 중요합니다.

위의 타원 정의에서 본 것처럼 타원의 임의 지점에서 초점 F까지의 거리와 같은 지점에서 초점 F’까지의 거리를 합하면 일정합니다. 음, 이 상수 값은 반장축이 측정하는 값의 두 배와 같습니다. 즉, 타원 위의 모든 점에 대해 다음과 같은 등식이 적용됩니다.

$d(P,F) + d(P,F')= 2a$

금

$d(P,F)$

그리고

$d(P,F')$

는 점 P에서 각각 초점 F와 F’까지의 거리입니다.

$a$

반초점축의 길이입니다.

따라서 보조 축의 꼭지점은 초점 축의 중앙에 있으므로 초점 중 하나까지의 거리는 준주 축의 길이와 동일합니다(

$a$

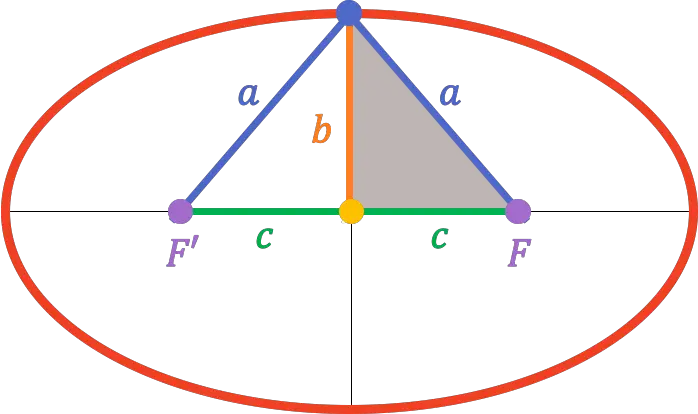
따라서 피타고라스 정리 에서 주 반축, 보조 반축 및 반 초점 거리 사이에 존재하는 관계를 찾는 것이 가능합니다.

$a^2=b^2+c^2$

이 공식은 타원을 사용한 연습 결과를 계산하는 데 매우 유용하므로 기억해 두십시오.

타원 이심률

분명히 모든 타원이 동일하지는 않지만 일부는 더 길고 다른 일부는 더 납작합니다. 따라서 주어진 타원이 얼마나 둥근지 측정하는 데 사용되는 계수가 있습니다. 이 계수를 이심률 이라고 하며 다음 공식으로 계산됩니다.

$e = \cfrac{c}{a}$

금

$c$

타원 중심에서 초점 중 하나까지의 거리입니다.

$a$

반장축의 길이.

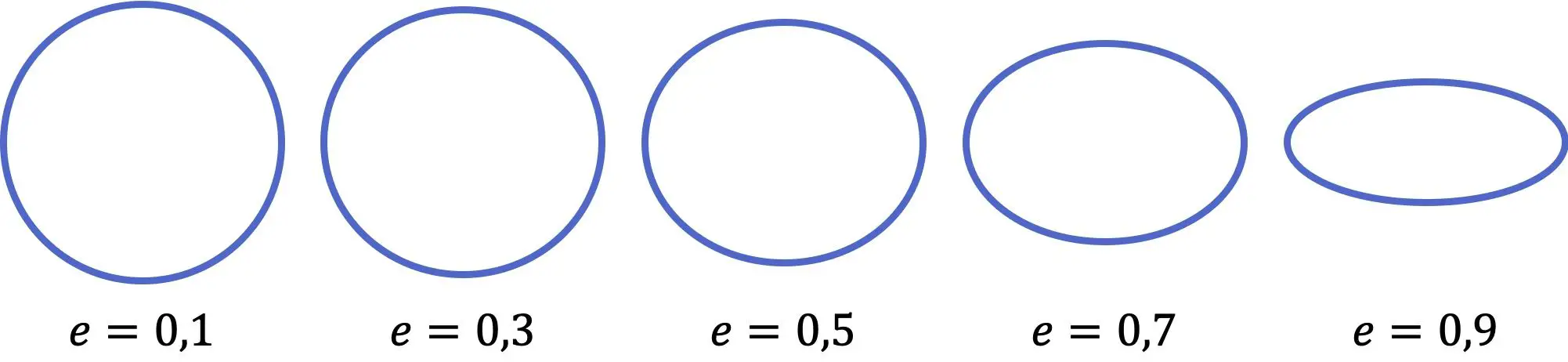
이전 표현에서 볼 수 있듯이 타원의 이심률 값이 작을수록 원에 더 가깝고, 계수가 클수록 타원이 더 평평해집니다. 또한 이심률 값의 범위는 0(완벽한 원)부터 1(수평선)까지이며 둘 다 포함되지 않습니다.

$0 <h2 class="wp-block-heading"><span class="ez-toc-section" id="ejemplo-de-como-calcular-la-ecuacion-de-la-elipse"></span> Exemple de calcul de l’équation de l’ellipse<span class="ez-toc-section-end"></span></h2> <p> Une fois que nous avons vu toutes les propriétés de l’ellipse, nous allons résoudre un problème d’ellipse à titre d’exemple :</p> <ul> <li> Trouver l’équation de l’ellipse dont le demi-axe principal mesure 5 unités (et est parallèle à l’axe OX), son centre est le point C(4,-1) et la distance de son centre à un foyer est de 4 unités.</li> </ul> <p> <strong>Pour déterminer l’équation d’une ellipse, nous avons besoin de la longueur du demi-axe principal, de la longueur du demi-axe secondaire et des coordonnées de son point.</strong> Par conséquent, dans ce cas, nous n’avons besoin de connaître que l’axe semi-secondaire. Ainsi, pour calculer la longueur mesurée par l’axe semi-secondaire, nous pouvons utiliser la relation entre l’axe semi-principal, l’axe semi-secondaire et la distance semi-focale : ” title=”Rendered by QuickLaTeX.com” height=”215″ width=”2133″ style=”vertical-align: -5px;”></p> <p> a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{5^2-4^2}=\sqrt {9} = 3</p> <p class=$ $Et une fois que l'on connaît la longueur des deux demi-axes et son centre, on peut trouver l'équation de l'ellipse à l'aide de sa formule :$

\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ bm{(y+1)^2}}{\bm{9}} \bm{= 1}

$<h2 class="wp-block-heading"><span class="ez-toc-section" id="ejercicios-resueltos-de-la-ecuacion-de-la-elipse"></span> Problèmes résolus de l’équation de l’ellipse<span class="ez-toc-section-end"></span></h2> <h3 class="wp-block-heading"> Exercice 1</h3> <p> Quelle est l’équation de l’ellipse centrée au point C(2,0) dont l’axe semi-principal (parallèle à l’axe X) et l’axe secondaire mesurent respectivement 6 et 3 unités ? Représenter graphiquement ladite ellipse. </p> <div class="wp-block-otfm-box-spoiler-start otfm-sp__wrapper otfm-sp__box js-otfm-sp-box__closed otfm-sp__E4F0FE" role="button" tabindex="0" aria-expanded="false" data-otfm-spc="#E4F0FE" style="text-align:center"> <div class="otfm-sp__title"> <strong>voir solution</strong></div> </div> <p> L’équation de l’ellipse est la suivante :” title=”Rendered by QuickLaTeX.com” height=”208″ width=”1595″ style=”vertical-align: -20px;”></p> <p> \cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1</p> <p class=$ $Par conséquent, à partir des données de l'énoncé, nous pouvons compléter l'équation de l'ellipse :$

\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}

$Et une fois que nous connaissons l'équation de l'ellipse, nous pouvons tracer la figure : <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="https://mathority.org/wp-content/uploads/2023/07/centre-de-lellipse-de-lequation-a-lexterieur-de-lorigine.webp" alt="équation de l'ellipse avec le centre hors de l'origine" class="wp-image-2106" width="524" height="368" srcset="" sizes=""></figure> </div> <div class="wp-block-otfm-box-spoiler-end otfm-sp_end"></div> <h3 class="wp-block-heading"> Exercice 2</h3> <p> Calculer l’équation de l’ellipse dont le demi-axe principal (parallèle à l’axe des abscisses) mesure 13 unités, son centre est l’origine des coordonnées et la distance de son centre à l’un de ses foyers est de 5 unités. </p> <div class="wp-block-otfm-box-spoiler-start otfm-sp__wrapper otfm-sp__box js-otfm-sp-box__closed otfm-sp__E4F0FE" role="button" tabindex="0" aria-expanded="false" data-otfm-spc="#E4F0FE" style="text-align:center"> <div class="otfm-sp__title"> <strong>voir solution</strong></div> </div> <p> Pour calculer l’équation de l’ellipse, nous devons savoir combien de temps mesure l’axe semi-secondaire. Et, pour cela, on peut utiliser la relation mathématique qui existe entre le demi-axe principal, le demi-axe secondaire et la demi-distance focale : ” title=”Rendered by QuickLaTeX.com” height=”299″ width=”2688″ style=”vertical-align: -20px;”></p> <p> a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{13^2-5^2}=\sqrt {144} = 12</p> <p class=$ $Et une fois que l'on connaît la longueur des deux demi-axes et son centre, on peut trouver l'équation de l'ellipse grâce à sa formule :$

\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\bm{144}} \bm{= 1}

$<div class="wp-block-otfm-box-spoiler-end otfm-sp_end"></div> <h3 class="wp-block-heading"> Exercice 3</h3> <p> Déterminer l’équation de l’ellipse suivante et les coordonnées de ses foyers : </p> <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="https://mathority.org/wp-content/uploads/2023/07/exercices-resolus-de-lequation-de-lellipse.webp" alt="exercices résolus pas à pas d'équations d'ellipses" class="wp-image-2111" width="533" height="404" srcset="" sizes=""></figure> </div> <div class="wp-block-otfm-box-spoiler-start otfm-sp__wrapper otfm-sp__box js-otfm-sp-box__closed otfm-sp__E4F0FE" role="button" tabindex="0" aria-expanded="false" data-otfm-spc="#E4F0FE" style="text-align:center"> <div class="otfm-sp__title"> <strong>voir solution</strong></div> </div> <p> Les sommets horizontaux de l’ellipse sont les points (-4,1) et (10,1). Par conséquent, son diamètre horizontal et son rayon sont : ” title=”Rendered by QuickLaTeX.com” height=”252″ width=”2047″ style=”vertical-align: -20px;”></p> <p> d_h=10-(-4) =14 a =\cfrac{14}{2} = 7</p> <p class=$ $De même, les sommets verticaux de l'ellipse sont les points (3,6) et (3,-4). Par conséquent, son diamètre vertical et son rayon sont :$

d_v=6-(-4) =10 b =\cfrac{10}{2} = 5

$Il suffit donc de trouver les coordonnées du centre de l'ellipse, qui correspondent aux milieux des extrémités de l'ellipse :$

C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1C(3.1)

$Enfin, l'équation de l'ellipse est :$

\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( y-1)^2}}{\bm{25}} \bm{= 1}

$D'autre part, la distance semi-focale vaut :$

a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}

$Cela signifie que les foyers de l'ellipse sont situés à une distance horizontale de$

\sqrt{24}

$unités du centre de l'ellipse, donc les coordonnées des foyers sont :$

C(3,1) \bm{F\left(3+\sqrt{24},1}\right)} \bm{F\left(3-\sqrt{24},1}\right)}

$<div class="wp-block-otfm-box-spoiler-end otfm-sp_end"></div> <h3 class="wp-block-heading"> Exercice 4</h3> <p> Calculez l’équation de l’ellipse qui répond aux caractéristiques suivantes :</p> <ul> <li> Son centre est l’origine des coordonnées du plan cartésien.</li> <li> Sa distance focale est égale à 6 unités.</li> <li> Un point de l’ellipse est à 3 et 5 unités de ses foyers. </li> </ul> <div class="wp-block-otfm-box-spoiler-start otfm-sp__wrapper otfm-sp__box js-otfm-sp-box__closed otfm-sp__E4F0FE" role="button" tabindex="0" aria-expanded="false" data-otfm-spc="#E4F0FE" style="text-align:center"> <div class="otfm-sp__title"> <strong>voir solution</strong></div> </div> <p> On peut calculer la demi-focale à partir de la focale : ” title=”Rendered by QuickLaTeX.com” height=”185″ width=”1667″ style=”vertical-align: -19px;”></p> <p> 2c = 6 c=\cfrac{6}{2} c=3</p> <p class=$ $D'autre part, on sait par la définition de l'ellipse que la somme des distances de chacun de ses points à ses foyers est équivalente à la longueur de son axe principal, donc :$

d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a

$Par conséquent, la longueur du demi-axe secondaire de l'ellipse vaut :$

a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}

$Et, en conclusion, l'équation de l'ellipse est :$

\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$

마지막으로, 이 기사가 도움이 되었다면 쌍곡선 공식 및 포물선 공식 에 대한 페이지에도 관심이 있으실 것입니다. 쌍곡선과 포물선이 무엇인지, 방정식, 특성, 예, 풀이 문제 등에 대한 자세한 설명을 찾을 수 있습니다.