여기에서는 함수 최적화 문제를 단계별로 해결하는 방법을 설명합니다. 또한 최적화 문제를 해결하는 연습문제도 연습할 수 있습니다.
최적화 문제란 무엇입니까?
최적화 문제는 함수의 최대값이나 최소값을 찾아야 하는 문제입니다. 예를 들어, 최적화 문제에는 회사의 이익을 정의하는 함수의 최대값을 계산하는 것이 포함됩니다.
최적화 문제를 해결하는 방법
함수 최적화 문제를 해결하는 단계:
- 최적화가 필요한 기능을 설정합니다 .
- 최적화할 함수를 도출합니다.
- 최적화할 함수의 임계점을 찾습니다. 이렇게 하려면 함수의 도함수를 0으로 설정하고 결과 방정식을 풀어야 합니다.
- 함수의 단조성을 연구하고 함수의 최대값 또는 최소값을 결정합니다.
최적화 문제의 예
최적화 문제 이론을 고려하여 이러한 유형의 문제를 단계별로 해결하여 어떻게 수행되는지 확인할 것입니다.
- 다리의 길이가 10cm인 직각삼각형 중에서 겉넓이가 가장 큰 직각삼각형의 크기를 구하여라.
문제를 해결하기 위해 삼각형의 한 가지를 x , 다른 가지를 y 라고 부릅니다.

1단계: 최적화할 기능을 설정합니다.
우리는 삼각형의 면적이 최대가 되길 원하며 삼각형의 면적에 대한 공식은 다음과 같습니다.
![]()
우리의 경우 삼각형의 밑변은 x 이고 높이는 y 입니다 . 아직:
![]()
우리는 이미 최적화할 함수를 가지고 있지만 두 개의 변수에 의존하지만 하나만 의존할 수 있습니다. 그러나 성명서에는 두 다리의 합이 10cm가 되어야 한다고 나와 있습니다. 아직:
![]()
다음 방정식에서 y를 구합니다.
![]()
그리고 표현식을 함수로 대체합니다.
![]()
![]()
이제 계획된 최적화 기능이 있고 하나의 변수에만 의존하므로 다음 단계로 넘어갈 수 있습니다.
2단계: 최적화할 함수의 도함수를 계산합니다.
이는 유리함수이므로 나눗셈의 도함수 공식을 적용하여 유도합니다.
![]()
![]()
3단계: 중요한 점을 찾으세요.
함수의 임계점을 찾으려면 도함수를 0으로 설정하고 결과 방정식을 풀어야 합니다.
![]()
![]()
4는 전체 왼쪽을 나누기 때문에 전체 오른쪽을 곱하여 곱할 수 있습니다.
![]()
![]()
![]()
![]()
![]()
4단계: 함수의 단조성을 연구하고 함수의 최대값 또는 최소값을 결정합니다.
함수의 단조로움을 연구하기 위해 오른쪽에 있는 임계점을 나타냅니다.
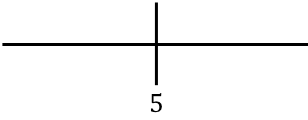
이제 각 간격에서 도함수의 부호를 평가하여 함수가 증가하는지 감소하는지 확인합니다. 이를 위해 우리는 각 구간에서 한 점(임계점은 아님)을 취하고 해당 점에서 도함수가 어떤 부호를 갖는지 살펴봅니다.
![]()
![]()
![]()
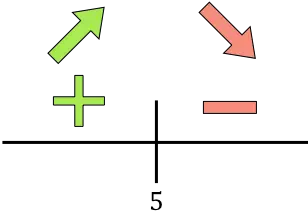
도함수가 양수이면 함수가 증가한다는 의미이고, 도함수가 음수이면 함수가 감소한다는 의미입니다. 따라서 함수의 증가 및 감소 간격은 다음과 같습니다.
성장:
![]()
감소하다:
![]()
x=5에서 함수는 증가에서 감소로 이동하므로 x=5는 최적화할 함수의 상대적 최대값입니다 .
따라서 x=5는 최대 면적을 갖는 삼각형 가지의 값입니다. 간단히 다른 쪽 다리의 값을 계산해 보세요.
![]()
결론적으로 삼각형의 최대 면적을 최대화하는 값은 다음과 같습니다.
![]()
![]()
최적화 문제가 해결되었습니다.
문제 1
아픈 사람에게 약을 주고,
![]()
몇 시간 후 활성 성분의 혈중 농도가 함수에 의해 제공됩니다.
![]()
밀리그램당 밀리그램. 최대값을 결정합니다.
![]()
해당 값에 도달하면 이를 나타냅니다.
1단계: 최적화할 기능을 설정합니다.
이 문제에서 그들은 이미 우리에게 제안된 함수를 제공했습니다.
![]()
2단계: 최적화할 함수의 도함수를 계산합니다.
함수는 2개의 함수의 곱으로 구성됩니다. 따라서 함수의 도함수를 계산하려면 곱의 도함수에 대한 규칙을 적용해야 합니다.
![]()
![]()
3단계: 중요한 점을 찾으세요.
함수의 임계점을 찾기 위해 다음을 해결합니다.
![]()
![]()
![]()
방정식을 풀기 위해 공통 요소를 사용합니다.
![]()
곱셈이 0이 되려면 곱셈의 두 요소 중 하나가 0이어야 합니다. 따라서 각 요소를 0으로 설정합니다.
![Rendered by QuickLaTeX.com \displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8390139724dbc4ad014db2a76e508290_l3.png)
따라서 다른 숫자로 승격된 숫자는 0이 될 수 없습니다.
![]()
해결책이 없습니다.
4단계: 함수의 단조성을 연구하고 함수의 최대값 또는 최소값을 결정합니다.
함수의 단조로움을 연구하기 위해 오른쪽에 있는 임계점을 나타냅니다.
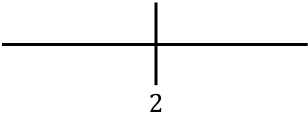
이제 각 간격에서 도함수의 부호를 평가하여 함수가 증가하는지 감소하는지 확인합니다. 따라서 우리는 각 구간에서 한 점(임계점은 아님)을 취하고 이 점에서 도함수가 어떤 부호를 갖는지 살펴봅니다.
![]()
![]()
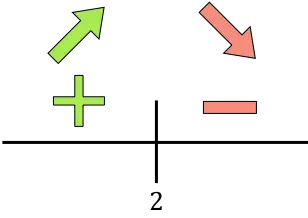
도함수가 양수이면 함수가 증가한다는 의미이고, 도함수가 음수이면 함수가 감소한다는 의미입니다. 따라서 최적화할 함수의 증가 및 감소 간격은 다음과 같습니다.
성장:
![]()
감소하다:
![]()
함수는 t=2에서 증가에서 감소로 이동하므로 t=2가 함수의 최대값입니다 . 따라서 최대 농도는 t=2시간 내에 도달합니다.
마지막으로 최대값이 발생하는 값을 원래 함수에 대입하여 최대 농도 값을 찾습니다.
![]()
문제 2
한 상점에서는 전기 스쿠터 40대를 스쿠터당 €1,000의 가격으로 판매하려고 합니다. 그러나 시장 조사에 따르면 스쿠터 가격이 50유로 인하될 때마다 상위 10대 베스트셀러 스쿠터의 판매가 증가할 것입니다.
먼저 스쿠터의 원래 가격인 $1,000가 $50만큼 감소한 횟수를 기반으로 매장의 수익 함수를 작성합니다. 다음으로, 최대 이익을 얻을 수 있는 스쿠터의 가격과 해당 가격에서 얻는 수익을 결정합니다.
1단계: 최적화할 기능을 설정합니다.
문제 진술은 초기 가격이 $50만큼 감소하는 횟수에 따라 함수가 달라져야 함을 알려주기 때문에 우리에게 단서를 제공합니다. 따라서 가격이 €50만큼 감소한 횟수를 x라고 하겠습니다.
![]()
€
수익 함수는 판매된 스쿠터 수에 각 스쿠터 가격을 곱한 값입니다.
![]()
판매되는 스쿠터 수는 40대 + 각 €50 가격 인하당 10대입니다. 아직:
![]()
각 스쿠터의 가격은 처음에는 €1000이며 가격이 인하될 때마다 €50씩 감소합니다. 아직:
![]()
따라서 문제를 최적화하는 기능은 다음과 같습니다.
![]()
![]()
![]()
![]()
2단계: 최적화할 함수의 도함수를 계산합니다.
다항식 함수이므로 도함수를 계산하기가 더 쉽습니다.
![]()
3단계: 함수의 임계점을 찾습니다.
함수의 임계점을 찾기 위해 다음을 해결합니다.
![]()
![]()
![]()
![]()
![]()
4단계: 함수의 단조성을 연구하고 함수의 최대값 또는 최소값을 결정합니다.
함수의 단조성을 연구하기 위해 수직선에 계산된 임계점을 나타냅니다.
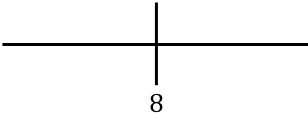
이제 각 간격에서 도함수의 부호를 평가하여 함수가 증가하는지 감소하는지 확인합니다. 따라서 우리는 각 구간에서 한 점(임계점은 아님)을 취하고 이 점에서 도함수가 어떤 부호를 갖는지 살펴봅니다.
![]()
![]()
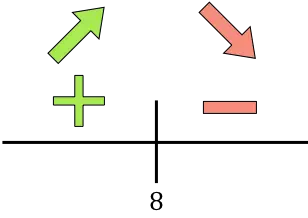
도함수가 양수이면 함수가 증가한다는 의미이고, 도함수가 음수이면 함수가 감소한다는 의미입니다. 따라서 성장 및 쇠퇴 간격은 다음과 같습니다.
성장:
![]()
감소하다:
![]()
함수는 x=8에서 증가에서 감소로 진행되므로 x=8은 함수의 최대값입니다 . 따라서 최대 수입은 €50 감소의 8배를 달성함으로써 얻을 수 있습니다.
이제 최대 소득이 나타나는 값을 원래 함수에 대입하여 최대 소득의 값을 찾습니다.
![]()
![]()
€
50유로 할인을 8회 수행한 후 각 스쿠터의 가격은 다음과 같습니다.
![]()
![]()
€
문제 3
회사의 비용 함수(천 유로 단위)는 다음 표현식을 사용하여 결정할 수 있습니다.
![]()
금
![]()
특정 품목이 생산된 수천 단위를 나타냅니다.
비용을 최소화하기 위해 얼마나 생산해야 하는지, 그 비용은 얼마인지, 이러한 품목 중 어느 것도 생산되지 않을 경우의 비용은 얼마인지 결정하십시오.
1단계: 최적화할 기능을 설정합니다.
문제 설명은 이미 최적화할 함수를 제공합니다.
![]()
2단계: 최적화할 함수의 도함수를 계산합니다.
![]()
3단계: 중요한 점을 찾으세요.
함수의 임계점을 찾기 위해 다음을 해결합니다.
![]()
![]()
![]()
![]()
![]()
4단계: 함수의 단조성을 연구하고 함수의 최대값 또는 최소값을 결정합니다.
우리는 오른쪽에 있는 중요한 점을 나타냅니다.
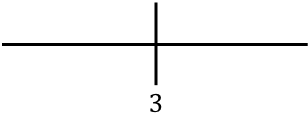
이제 각 간격에서 도함수의 부호를 평가하여 함수가 증가하는지 감소하는지 확인합니다. 따라서 우리는 각 구간에서 한 점(임계점은 아님)을 취하고 이 점에서 도함수가 어떤 부호를 갖는지 살펴봅니다.
![]()
![]()
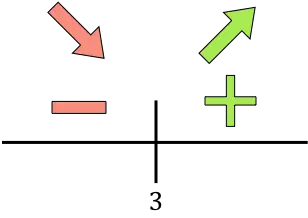
도함수가 0보다 크면 이 구간에 걸쳐 함수가 증가합니다. 반면에 도함수가 0보다 작으면 이 구간에서 함수가 감소합니다. 따라서 함수의 증가 및 감소 간격은 다음과 같습니다.
성장:
![]()
감소하다:
![]()
함수는 x=3에서 감소에서 증가로 이동하므로 x=3은 함수의 최소값입니다 . 따라서 최소비용은 3,000개 생산으로 달성하게 된다.
이제 최소 비용에 도달한 값을 원래 함수에 대체하여 최소 비용 값을 찾습니다.
![]()
수백만 유로.
반면에 그들은 아무것도 생산되지 않으면 비용이 얼마인지 묻습니다.
![]()
그러므로 계산이 필요하다.
![]()
![]()
수백만 유로.
문제 4
우리는 2m 2 의 면적을 제한하는 직사각형 나무 프레임을 만들고 싶습니다. 우리는 목재 가격이 수평면의 경우 €7.5/m, 수직면의 경우 €12.5/m라는 것을 알고 있습니다. 프레임의 총 비용이 가능한 최소가 되고 해당 비용도 최소가 되도록 직사각형이 가져야 하는 치수를 결정합니다.
1단계: 최적화할 기능을 설정합니다.
문제를 해결하기 위해 가로 변을 x , 세로 변을 y 라고 합니다.

가로면 구매 비용은 7.5유로, 세로면 구매 비용은 12.5유로입니다. 또한 각 프레임에는 수평 측면 2개와 수직 측면 2개가 필요합니다. 따라서 프레임 비용은 다음 기능을 사용하여 결정할 수 있습니다.
![]()
우리는 이미 최적화 기능을 갖고 있습니다. 그러나 하나의 변수에만 의존할 수 있는 경우에는 두 개의 변수에 의존합니다. 그러나 성명서는 프레임의 표면적이 2m 2 여야 함을 알려줍니다. 아직:
![]()
변수 y를 삭제합니다.
![]()
그리고 최적화할 함수에서 찾은 표현식을 다음과 같이 대체합니다.
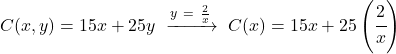
![]()
2단계: 최적화할 함수의 도함수를 계산합니다.
![]()
3단계: 중요한 점을 찾으세요.
함수의 임계점을 찾기 위해 다음을 해결합니다.
![]()
![]()
![]()
![]()
![]()
![]()
분수로 방정식을 풀기 위해 가로로 곱합니다.
![]()
![]()
![]()
![]()
![]()
4단계: 함수의 단조성을 연구하고 함수의 최대값 또는 최소값을 결정합니다.
우리는 라인에서 함수의 단조로움을 분석하기 위해 발견된 임계점을 나타냅니다.
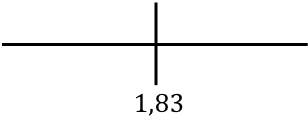
이제 각 간격에서 도함수의 부호를 평가하여 함수가 증가하는지 감소하는지 확인합니다. 따라서 우리는 각 구간에서 한 점(임계점은 아님)을 취하고 이 점에서 도함수가 어떤 부호를 갖는지 살펴봅니다.
![]()
![]()
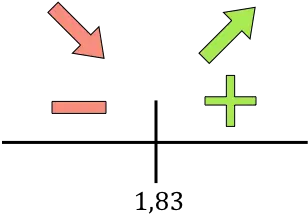
도함수가 양수이면 함수가 증가한다는 의미이고, 도함수가 음수이면 함수가 감소한다는 의미입니다. 따라서 성장 및 쇠퇴 간격은 다음과 같습니다.
성장:
![]()
감소하다:
![]()
함수는 x=1.83에서 감소에서 증가로 변경되므로 x=1.83은 함수의 최소값입니다 .
따라서 x=1.83은 최소비용을 나타내는 가로변의 값이다. 이제 수직 변의 값을 계산해 보겠습니다.
![]()
따라서 최소 프레임워크 비용을 구성하는 값은 다음과 같습니다.
수평면
![]()
수직면
![]()
이 값으로 도달한 최소 비용은 다음과 같습니다.
![]()
€
문제 5
대성당의 문은 다음 그림과 같이 두 개의 기둥으로 지지되는 반원형 아치로 구성됩니다.
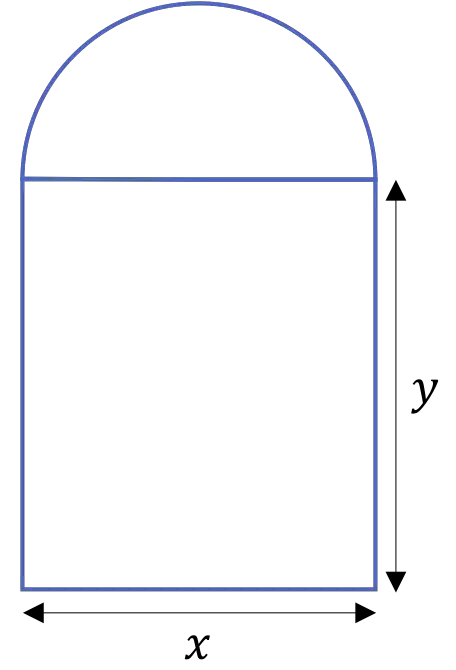
문의 둘레가 20m인 경우 측정값을 결정합니다.
![]()
그리고
![]()
도어 전체의 표면적을 극대화합니다.
1단계: 최적화할 기능을 설정합니다.
원의 면적은 다음 공식으로 계산됩니다.
![]()
따라서 전체 문의 면적은 직사각형 면적에 원주 면적의 절반을 더한 값이 됩니다.
![]()
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-baa2e14b061cf14a657782db8fe91b92_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9196d8284edebe6450d49aa5a0b6a3e1_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-b25e1d2c661585be998d1596d6650c01_l3.png)
![]()
우리는 이미 최적화 기능을 갖고 있습니다. 그러나 하나의 변수에만 의존할 수 있는 경우에는 두 개의 변수에 의존합니다.
하지만 공개된 내용에 따르면 전체 게이트의 둘레는 20m라고 합니다. 원의 둘레는 공식으로 계산됩니다.
![]()
따라서 전체 문의 둘레는 다음과 같습니다.
![Rendered by QuickLaTeX.com P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }](https://mathority.org/wp-content/ql-cache/quicklatex.com-7709d0c72bf84a17ac83bc46f5cce002_l3.png)
둘레는 20m 여야합니다. 따라서 우리는 이전 표현식을 20으로 설정하여 사이의 관계를 찾습니다.
![]()
그리고
![]()
![]()
분수를 제거하기 위해 모든 항에 2를 곱합니다.
![]()
![]()
클리어한다
![]()
![]()
![]()
그리고 최적화할 함수에서 찾은 표현식을 다음과 같이 대체합니다.
![]()
![]()
![]()
2단계: 최적화할 함수의 도함수를 계산합니다.
![]()
![]()
3단계: 중요한 점을 찾으세요.
함수의 임계점을 찾기 위해 다음을 해결합니다.
![]()
![]()
![]()
이것은 분수가 있는 방정식이므로 각 항에 분모의 lcm을 곱하여 분수를 제거합니다.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4단계: 함수의 단조성을 연구하고 함수의 최대값 또는 최소값을 결정합니다.
함수의 단조로움을 연구하기 위해 오른쪽에 있는 임계점을 나타냅니다.
이제 각 간격에서 도함수의 부호를 평가하여 함수가 증가하는지 감소하는지 확인합니다. 따라서 우리는 각 구간에서 한 점(임계점은 아님)을 취하고 이 점에서 도함수가 어떤 부호를 갖는지 살펴봅니다.
![]()
![]()
도함수가 양수이면 함수가 증가한다는 의미이고, 도함수가 음수이면 함수가 감소한다는 의미입니다. 따라서 성장 및 쇠퇴 간격은 다음과 같습니다.
성장:
![]()
감소하다:
![]()
함수는 x=5.6에서 증가에서 감소로 이동하므로 x=5.6은 함수의 최대값입니다 .
아직,
![]()
최대 표면을 이루는 값입니다. 이제 우리는
![]()
![]()
따라서 최대 표면을 구성하는 값은 다음과 같습니다.
![]()
![]()
문제 6
우리는 54 cm 2 면적의 원통형 탱크를 만들고 싶습니다. 부피가 최대가 되도록 밑면의 반경과 원통의 높이를 결정합니다.
1단계: 최적화할 기능을 설정합니다.
실린더의 부피는 다음 공식으로 계산됩니다.
![]()
밑면의 넓이는 원이므로 그 공식은 다음과 같습니다.
![]()
. 따라서 실린더의 부피 공식은 다음과 같습니다.
![]()
우리는 이미 최적화 기능을 갖고 있습니다. 그러나 이는 두 가지 변수에 따라 달라집니다(
![]()
그리고
![]()
) 단 하나에만 의존할 수 있습니다. 그러나 이 진술은 원통의 면적이 54 cm 2 여야 함을 말하므로 우리는 이 조건을 활용하여 두 사이의 관계를 찾을 것입니다.
![]()
그리고
![]()
원통의 면적을 계산하려면 두 밑면의 면적에 측면 면적을 더해야 합니다.
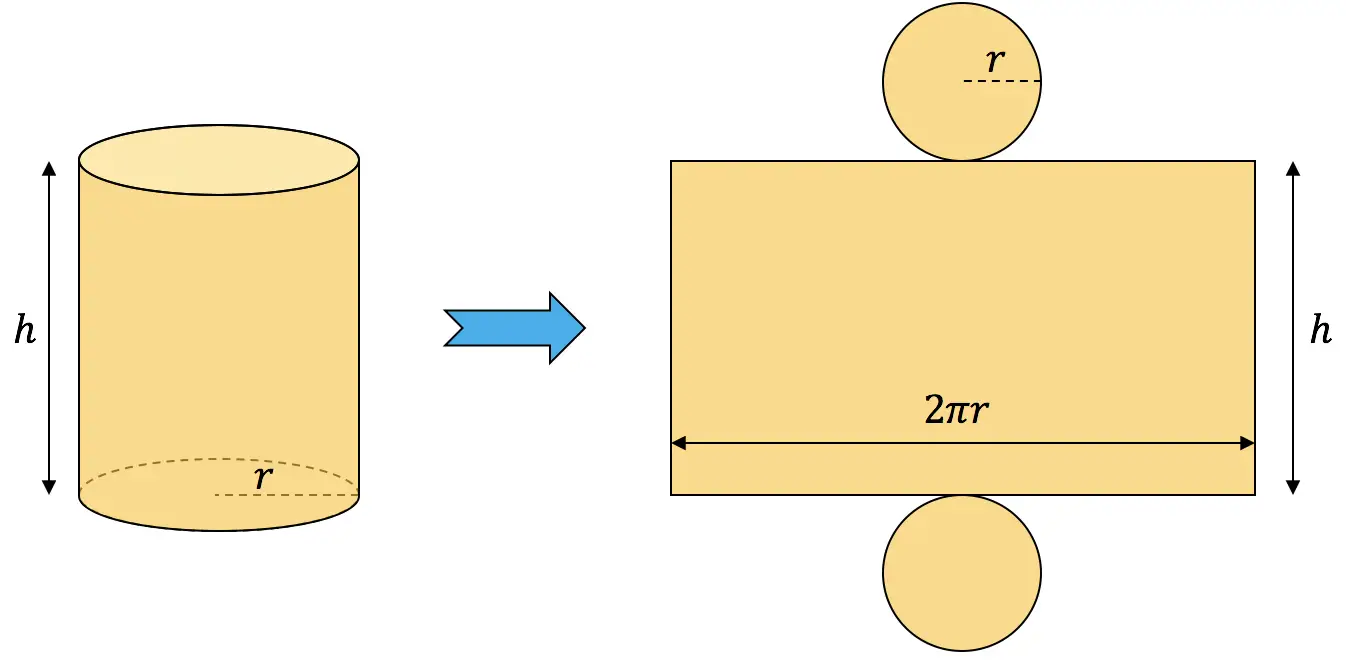
![]()
원통의 면적은 54 cm 2 여야 하므로 이전 식을 54로 설정하여 두 사이의 관계를 얻습니다.
![]()
그리고
![]()
![]()
클리어한다
![]()
![]()
![]()
그리고 최적화할 함수에서 찾은 표현식을 다음과 같이 대체합니다.
![]()
![]()
![]()
2단계: 최적화할 함수의 도함수를 계산합니다.
![]()
3단계: 중요한 점을 찾으세요.
함수의 임계점을 찾기 위해 다음을 해결합니다.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4단계: 함수의 단조성을 연구하고 함수의 최대값 또는 최소값을 결정합니다.
함수의 단조성을 연구하기 위해 수직선에 있는 임계점을 나타냅니다.
이제 각 간격에서 도함수의 부호를 평가하여 함수가 증가하는지 감소하는지 확인합니다. 따라서 우리는 각 구간에서 한 점(임계점은 아님)을 취하고 이 점에서 도함수가 어떤 부호를 갖는지 살펴봅니다.
![]()
![]()
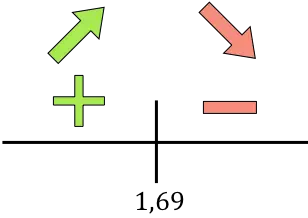
도함수가 양수이면 함수가 증가한다는 의미이고, 도함수가 음수이면 함수가 감소한다는 의미입니다. 따라서 성장 및 쇠퇴 간격은 다음과 같습니다.
성장:
![]()
감소하다:
![]()
함수는 r=1.69에서 증가에서 감소로 이동하므로 r=1.69cm가 함수의 최대값입니다 .
따라서 r=1.69는 부피가 최대가 되는 반경의 값이다. 이제 높이를 계산합니다.
![]()
따라서 최대 볼륨을 만드는 값은 다음과 같습니다.
라디오
![]()
키
![]()