여기에서는 쌍곡선 사인(공식)을 유도하는 방법을 찾을 수 있습니다. 또한 쌍곡사인 도함수에 대한 몇 가지 해결된 예를 볼 수 있습니다. 그리고 마지막으로 이러한 유형의 삼각 함수의 미분 공식을 증명합니다.
쌍곡사인에서 파생된 공식
x의 쌍곡선 사인의 도함수는 x의 쌍곡선 코사인입니다.
![]()
따라서 함수의 쌍곡선 사인의 도함수는 해당 함수의 쌍곡선 코사인과 해당 함수의 도함수의 곱과 같습니다.
![]()
실제로 위의 두 공식은 동일하며 유일한 차이점은 두 번째 공식에서는 체인 규칙을 적용한다는 것입니다. 그리고 x의 미분은 1이므로 함수는 변경되지 않습니다.
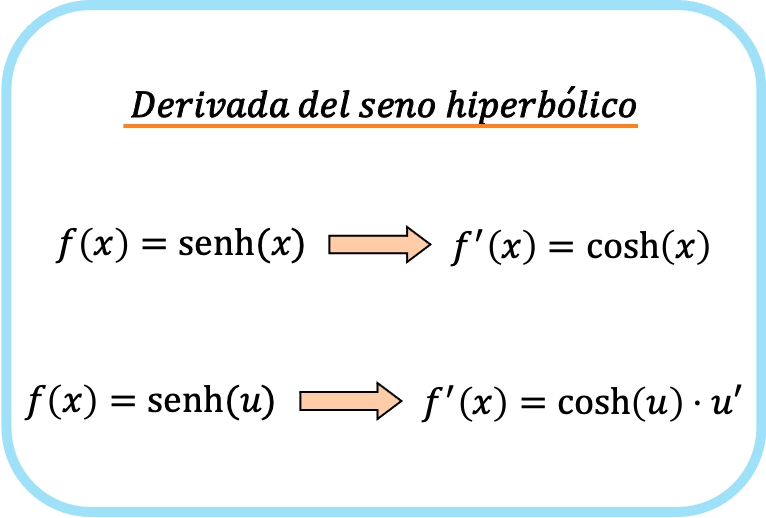
보시다시피, 쌍곡선 사인 도함수 공식은 사인 도함수 공식 과 매우 유사합니다.
쌍곡사인 파생물의 예
쌍곡선 사인 파생 공식이 무엇인지 이미 살펴보았으면 이제 쌍곡선 사인 파생의 몇 가지 예를 해결해 보겠습니다. 따라서 이것이 어떻게 수행되는지에 대해 의심의 여지가 없습니다.
예 1: 2x 쌍곡사인의 파생
![]()
이 경우, 쌍곡사인 인수에서는 x와 다른 함수를 가지므로, 도함수를 찾기 위해 연쇄 법칙과 함께 쌍곡선 사인 도함수 공식을 사용해야 합니다:
![]()
2x의 도함수는 2이므로, 2x의 쌍곡사인의 도함수는 2x 곱하기 2의 쌍곡코사인이 됩니다.
![]()
예 2: x 제곱의 쌍곡선 사인 파생
![]()
쌍곡사인 함수의 미분 공식은 다음과 같습니다.
![]()
반면에 이차 함수 x 2 의 미분은 2x입니다. 따라서 전체 함수의 미분은 다음과 같습니다.
![]()
쌍곡사인의 도함수에 대한 공식 증명
마지막으로 쌍곡사인 도함수에 대한 공식을 보여드리겠습니다. 이를 위해 쌍곡사인의 수학적 정의부터 시작하겠습니다.
![]()
이제 우리는 평등의 양면을 추론합니다.
![]()
방정식의 우변을 도출하기 위해 나눗셈의 미분 공식을 사용합니다.
![]()
➤ 참조: e를 밑으로 하는 지수 함수의 도함수
그리고 정확하게 우리는 쌍곡선 코사인을 정의하는 표현에 도달했습니다. 쌍곡사인의 미분은 다음과 같이 증명됩니다.
![]()