이 기사에서는 선형 함수의 도함수가 얼마인지 보여줍니다. 또한 선형 함수의 도함수에 대한 몇 가지 예를 풀고 이러한 유형의 도함수에 대한 공식을 보여줍니다. 선형 함수의 도함수에 대한 해결된 연습 문제도 찾을 수 있습니다.
선형 함수의 미분은 무엇입니까?
선형 함수의 도함수는 1차 항의 계수입니다 . 즉, 선형 함수 f(x)=Ax+B 의 도함수는 A 와 같습니다.
![]()
상수 의 도함수가 0이기 때문에 독립항은 도함수 에서 제거됩니다. 반면에 1차 항의 도함수는 해당 항의 계수입니다. 따라서 이 두 가지 유형의 함수의 합의 도함수는 선형 항의 계수입니다.
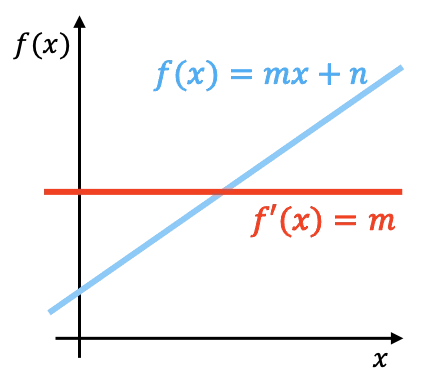
기하학적으로 선형 함수의 미분은 해당 함수의 기울기입니다. 위의 그래프에서는 도함수가 포함된 선형 함수가 표시되는 것을 볼 수 있습니다.
선형 함수의 도함수 예
선형 함수의 도함수 정의를 바탕으로 선형 함수의 몇 가지 예를 계산하여 개념 이해를 마무리하겠습니다.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b12cfa0a6432f8171149ec0139d259ce_l3.png)
선형 함수의 도함수는 함수에 독립 항이 없는 경우, 즉 1차 항이 하나만 있는 경우 항상 변수 x에 수반되는 숫자라는 점을 명심하세요. 예를 들어:
![]()
따라서 선형함수의 미분은 독립변수가 없는 단순한 숫자의 함수이다.
선형 함수의 미분 증명
다음으로 선형 함수의 미분 공식을 보여드리겠습니다.
f를 임의의 선형 함수로 둡니다.
![]()
한 점에서 함수의 도함수를 계산하는 공식은 다음과 같습니다.
![]()
따라서 선형 함수의 이전 극한을 계산하면 다음과 같은 결과를 얻습니다.
![]()
괄호를 해결합니다.
![]()
우리는 분자에서 작동합니다:
![]()
마지막으로 분수를 단순화합니다.
![]()
결론적으로, 선형 함수의 도함수는 임의의 점에서 1차 항의 계수와 같습니다. 따라서 선형 함수의 미분 공식이 도출됩니다.
선형 함수의 도함수 문제 해결
다음 선형 함수의 도함수를 계산합니다.
![]()
![]()
![]()
![]()
![]()
![]()
선형 함수를 도출하려면 함수에서 상수항과 변수를 제거하여 선형항의 계수만 남게 하면 됩니다. 아직:
![]()
![]()
![]()
![]()
![]()
![]()
함수의 계수는 분수나 근이지만 선형 함수의 유도도 같은 방식으로 수행됩니다.