이 페이지에서는 그래픽적으로나 수치적으로 두 벡터를 뺄셈하는 방법을 볼 수 있습니다. 이를 그래픽적으로 빼는 방법에는 평행사변형, 삼각형, 다각형의 세 가지 방법이 있습니다. 여기서 각 방법의 장점과 단점을 구분할 수 있습니다. 또한 단계별로 예제, 연습 문제 및 해결된 문제를 찾을 수 있습니다.
두 벡터를 그래픽적으로 빼는 방법은 무엇입니까?
벡터를 기하학적으로 빼는 방법에는 여러 가지가 있습니다. 분명히, 모두 동일한 결과를 얻지만, 귀하가 선호하는 방법을 선택할 수 있도록 모든 방법을 설명하겠습니다. 👌
2개의 벡터만 빼려면 평행사변형 방법 과 삼각형 방법 이라는 두 가지 그래픽 절차가 있습니다. 그러나 3개 이상의 벡터의 뺄셈을 풀고 싶다면 폴리곤 방법을 사용해야 합니다.
따라서 더 이상 고민하지 않고 아래에서 이러한 모든 방법에 대한 설명을 볼 수 있습니다.
평행사변형 방법 또는 규칙
평행사변형 규칙 또는 평행사변형 방법은 그래픽 표현을 통해 매우 간단한 방법으로 두 벡터의 뺄셈을 찾을 수 있는 절차입니다. 이 프로세스를 적용하기 위해 따라야 할 단계는 다음과 같습니다.
- 먼저, 그래프에 두 벡터를 나타내고 이를 동일한 적용 지점에 배치합니다. 즉, 두 벡터의 원점을 동일한 지점에 배치합니다.
- 둘째, 연산에서 빼는 벡터의 반대 벡터를 그린다. 즉, 빼는 벡터를 반전시킨다.
- 그런 다음 추가된 벡터의 끝에 부호가 변경된 벡터와 평행한 선을 그립니다. 그리고 우리는 다른 벡터로 이 과정을 반복합니다. 그래서 우리는 평행사변형의 그림을 얻을 것입니다(따라서 규칙의 이름).
- 마지막으로 뺄셈의 결과는 두 벡터의 공통 원점에서 두 평행선이 교차하는 지점까지 가는 벡터가 됩니다.
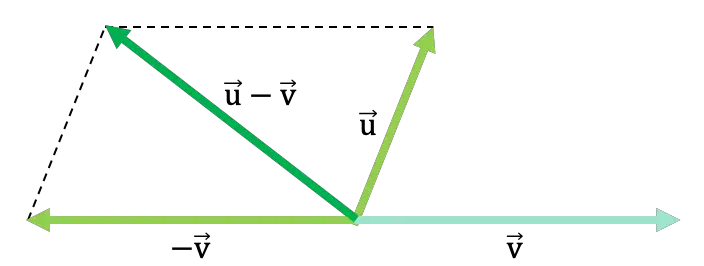
평행사변형 방법을 사용하여 두 벡터를 빼는 다음의 일반적인 예를 고려하십시오.
삼각형 방법 또는 규칙
삼각형 방법은 그래프에서 두 벡터를 뺄 수 있는 또 다른 절차입니다. 이 경우 따라야 할 단계는 다음과 같습니다.
- 두 벡터를 동일한 적용 지점에 배치합니다. 즉, 두 벡터가 원점과 동일한 지점을 갖도록 합니다.
- 벡터 뺄셈의 결과는 뺄셈 벡터의 끝에서 다른 벡터의 끝으로 가는 세그먼트입니다. 자세히 보면 두 벡터를 빼고 벡터를 빼서 삼각형이 완성됩니다.
다음은 삼각형 방법을 사용한 벡터 빼기의 예입니다.
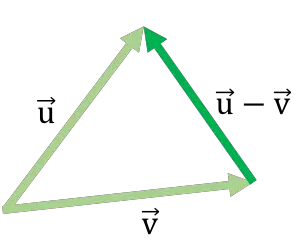
벡터를 빼는 이 방법은 벡터를 더하는 데 사용되는 머리 및 꼬리 방법 과 유사합니다.
다각형 방법
두 벡터의 뺄셈을 그래픽으로 해결하는 방법을 살펴본 후에는 두 개 이상의 벡터가 있을 때 어떻게 수행되는지 살펴보겠습니다.
3개 이상의 벡터를 빼고 싶을 때 계산 속도를 더 빠르게 하여 모든 벡터를 한꺼번에 빼는 기술이 있습니다. 이 기법을 폴리곤법 이라고 하며, 벡터 덧셈의 Head-to-Tail 방식을 연속적으로 적용하는 방식으로 구성됩니다.
이제 당신은 아마도 다음과 같이 생각하고 있을 것입니다: 벡터를 추가하는가 ? 잘못 수정됐네요… 글쎄요! 에 에
두 벡터를 빼는 것은 벡터에 빼는 벡터의 반대(또는 음의) 벡터를 더하는 것과 동일하다는 것이 밝혀졌습니다. 이는 벡터의 덧셈과 뺄셈 속성 때문입니다.
![]()
따라서 다각형 방법을 사용하여 3개 이상의 벡터를 빼기 위해 따라야 하는 단계는 다음과 같습니다.
- 먼저, 각 빼기 벡터의 역벡터를 찾아야 합니다. 빼는 모든 벡터의 방향과 방향을 반대로 바꾸는 것만 큼 간단합니다.
- 그런 다음 빼지 않는 벡터 옆에 각각 반대 벡터를 하나씩 배치합니다. 벡터의 원점은 다른 벡터의 끝과 일치합니다.
- 마지막으로 벡터 빼기의 결과는 첫 번째 벡터의 시작과 마지막 벡터의 끝을 결합한 벡터입니다.
4개의 벡터를 사용하여 뺄셈을 수행하는 다음 예를 살펴보십시오.
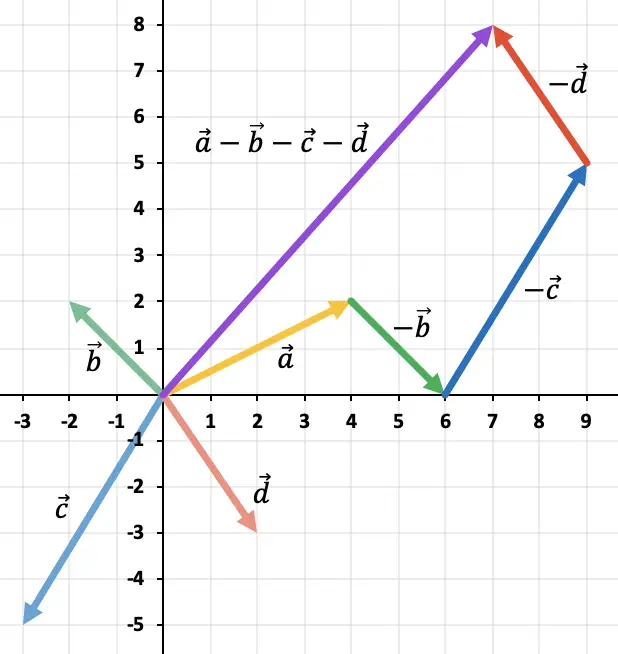
벡터의 반대 벡터를 찾으려면 해당 벡터의 두 구성 요소의 부호가 변경되어야 합니다.
두 벡터의 뺄셈을 수치적으로 계산하는 방법은 무엇입니까?
그래프에서 벡터를 뺄셈하는 방법을 이미 알고 나면 수치적 또는 대수적으로 벡터 뺄셈을 계산하는 방법을 살펴보겠습니다.
두 벡터를 수치적으로 빼려면 해당 구성요소를 빼야 합니다. 즉, 두 벡터의 X 좌표를 서로 빼는 것과 마찬가지로 Y 좌표도 마찬가지입니다.
![]()
![]()
예를 들어 벡터 사이의 뺄셈
![]()
그리고
![]()
동쪽:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(4,1) -(2, 3) \\[2ex] & = (4-2,1-3) \\[2ex] & = \bm{(2,-2)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5497555b19f5d230433a622a03704ee_l3.png)
벡터 빼기 문제 해결
연습 1
벡터 빼기를 그래픽으로 계산
![]()
더 적은
![]()
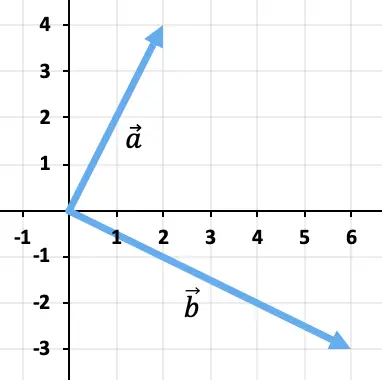
두 벡터를 빼기 위해 삼각형 방법을 사용합니다. 점은 이미 동일한 적용점(좌표의 원점)에 배치되어 있으므로 빼기 결과는 끝에서 이동하는 벡터가 됩니다.
![]()
끝에
![]()
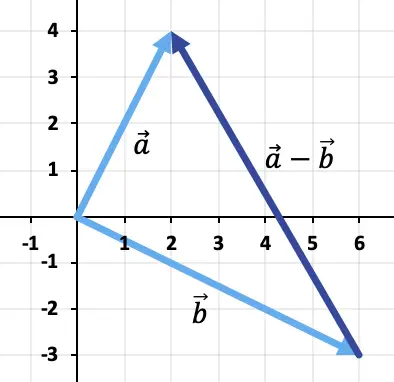
연습 2
그래픽을 통해 벡터의 뺄셈 찾기
![]()
더 적은
![]()
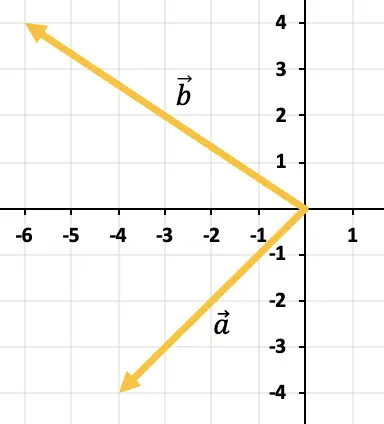
두 벡터를 빼기 위해 삼각형 규칙을 사용합니다. 점은 이미 동일한 적용점(X축과 Y축의 시작점)에 배치되어 있으므로 빼기 결과는 끝점에서 이동하는 벡터가 됩니다.
![]()
끝에
![]()
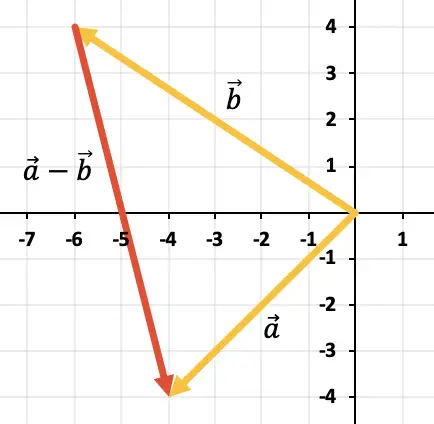
연습 3
다음 벡터 연산을 그래픽으로 풀어보세요.
![]()
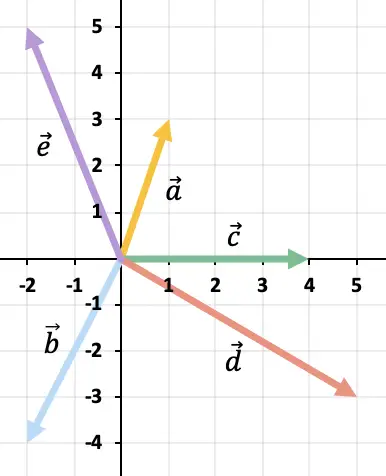
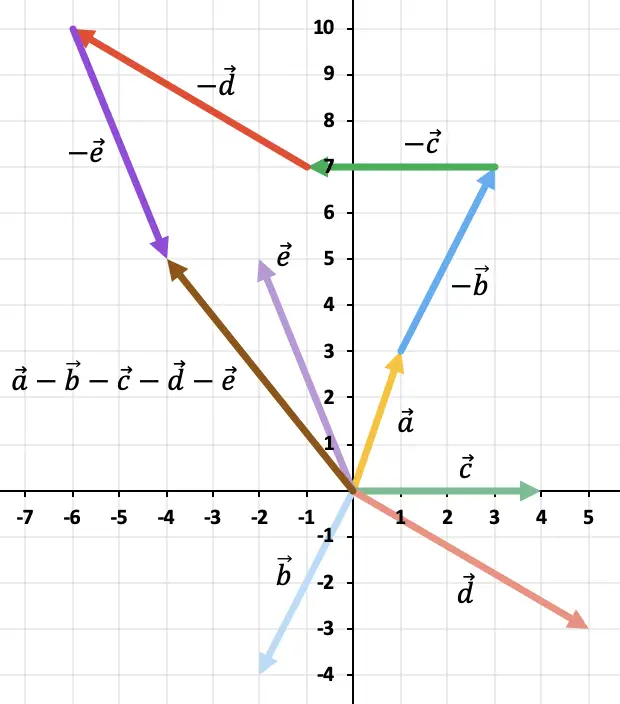
벡터가 2개 이상 있으므로 다각형 규칙을 사용하여 벡터 빼기를 해결하겠습니다. 이를 위해서는 나머지 벡터의 반대 벡터를 차례로 표현해야 합니다. 결과는 벡터의 원점에서 시작하는 벡터가 됩니다.
![]()
마지막 반대 벡터가 끝나는 곳으로.
연습 4
다음 벡터를 뺀 결과를 수치적으로 결정합니다.
![]()
![]()
두 벡터를 수치적으로 빼려면 해당 좌표를 빼야 합니다.
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}-\vv{b}& =(-1,5)-(3,-2) \\[2ex] & = (-1-3 ,5-(-2))\\[2ex] & = (-4 ,5+2)\\[2ex] & =\bm{(-4,7)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b64aac805c6565b57ac1d33977988013_l3.png)
연습 5
다음 벡터 연산을 분석적으로 풀어보세요.
![]()
![]()
수치적으로(또는 분석적으로) 벡터를 빼려면 해당 구성요소를 빼야 합니다.
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}-\vv{b}-\vv{d}-\vv{d}& =(2,4)-(-1,4)-(0,2)-(3,-7) \\[2ex] & =(3,0)-(0,2)-(3,-7) \\[2ex] & =(3,-2)-(3,-7) \\[2ex]& =\bm{(0,5)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fa640e47728e968a9626c295f237f93c_l3.png)