무한대 사이의 무한 불확정성(무한대/무한대)

이 기사에서는 무한대(무한대/무한대) 사이의 불확정성의 무한대를 계산하는 방법을 설명합니다. 다항식, 근호, 지수 함수 등 모든 종류의 함수에서 이러한 불확정의 예를 찾을 수 있습니다. 또한 무한 사이에 무한한 불확정을 제공하는 한계를 단계별로 해결하는 연습을 통해 훈련할 수 있습니다.

무한 사이의 무한 불확정성을 해결하는 방법

함수의 극한이 무한대를 무한대로 나눈다는 것은 그것이 불확정성(또는 불확정 형식)임을 의미합니다. 무한대 사이의 불확정성을 부여하는 함수의 극한을 풀려면 분자 다항식의 차수와 분모 다항식의 차수를 비교해야 합니다.

$\displaystyle\lim_{x\to +\infty}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\frac{+\infty}{+\infty}$

불확정성 무한대를 무한대로 나눈 결과는 분수의 분자 차수와 분모 차수에 따라 달라집니다.

분자 다항식의 차수가 분모 다항식의 차수보다 작은 경우, 불확정성의 무한대를 무한대로 나눈 값은 0과 같습니다.
분자 다항식의 차수가 분모 다항식의 차수와 동일하면 무한대에 대한 무한 불확정성은 두 다항식의 최고차 계수의 몫입니다.
분자 다항식의 차수가 분모 다항식의 차수보다 큰 경우, 무한대 사이의 불확정의 무한대는 다소 무한대를 제공합니다(부호는 두 다항식의 주요 항에 따라 다름).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> <h2 class=$ 무한대 사이의 무한 불결정의 예

각 경우의 몇 가지 예를 살펴봄으로써 무한 사이의 불확정 형태 무한이 어떻게 해결되는지 살펴보겠습니다.

분모의 차수보다 작은 분자의 차수

위에서 본 것처럼, 분자 다항식의 차수가 분모 다항식의 차수보다 작을 때, 무한대 사이의 무한 무한 극한은 항상 0을 제공합니다.

예시 1:

$\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

분자의 다항식은 2차이고 분모의 다항식은 3차이므로 극한의 해는 0입니다.

예 2:

$\displaystyle \lim_{x \to -\infty} \frac{-7x}{2x^4+3x^2}=\frac{-7\cdot (-\infty)}{2(-\infty)^4}=\frac{+\infty}{+\infty}= \bm{0}$

분자의 다항식 함수는 1차이지만 분모의 함수는 4차이므로 음의 무한대의 한계는 0입니다.

분자의 차수는 분모의 차수와 같습니다.

분자 다항식의 차수가 분모 다항식의 차수와 같을 때, 두 다항식의 최고차 계수(고차항의 계수)를 나누어 무한한계 무한대를 계산합니다.

예시 3:

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

이 경우 두 다항식은 2차이므로 양의 무한대에서 극한을 찾기 위해 더 높은 차수의 항의 계수를 나누어야 합니다.

예시 4:

$\displaystyle \lim_{x \to -\infty} \cfrac{2x+1}{5x+3} = \cfrac{2(-\infty)}{5(-\infty)}= \cfrac{-\infty}{-\infty} =\cfrac{\bm{2}}{\bm{5}}$

극한은 x가 음의 무한대에 가까워지는 경우이지만, 무한대 사이의 무한 불확정성은 같은 방식으로 해결됩니다.

분모의 차수보다 분자의 차수가 더 큽니다.

분자 다항식의 차수가 분모 다항식의 차수보다 큰 경우, 무한대 사이의 무한대의 부정형 형태는 항상 무한대를 제공하며, 무한대의 부호는 두 다항식의 더 높은 차수의 항에 의해 결정됩니다.

예시 5:

$\displaystyle \lim_{x \to +\infty} \cfrac{x^2+7}{x-2} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

분자의 함수는 분모의 함수보다 더 높은 차수를 가지므로 무한대에 대한 불확정성 무한대는 무한대를 제공합니다. 또한 이 경우 분자와 분모는 모두 양의 무한대를 가지므로 극한의 결과도 양수여야 합니다.

예시 6:

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

이 문제에서는 임의의 제곱항이 양수이기 때문에 분자로부터 양의 무한대를 얻는 반면, 분모에서는 음의 무한대를 얻습니다. 따라서 양수를 음수로 나눈 값은 음수이므로 결과 한계는 음수입니다.

근과 무한 사이의 무한 불확정성

우리는 다항식 함수가 있을 때 무한대 사이의 무한 불확정성을 계산하는 방법을 방금 살펴보았습니다. 그런데… 뿌리가 있다면 무한대를 무한대로 나누면 얼마나 될까요?

무리함수(근이 있는 함수)의 차수는 주항의 차수와 근호 지수 사이의 몫입니다.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

따라서 근이 있는 함수의 극한이 무한대 간의 불확정성을 제공하는 경우 분자와 분모의 차수에 대해 위에서 설명한 것과 동일한 규칙을 적용해야 합니다. 단, 근이 있는 다항식의 차수는 다르게 계산된다는 점을 고려해야 합니다.

근호가 있는 함수의 무한대 극한에 대한 다음 예를 살펴보십시오.

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

분자의 차수는 2이고 분모의 차수는 4(8/2=4)이므로 분자의 차수가 분모의 차수보다 작으므로 극한은 0입니다.

반면, 분자와 분모의 차수가 같은 경우, 불확정 극한을 계산하려면 근호를 사용하여 주 계수를 취해야 합니다.

$\displaystyle\lim_{x\to +\infty}\frac{6x-5}{\sqrt{9x^2+2x}}=\frac{6(+\infty)}{\sqrt{9(+\infty)^2}}=\frac{+\infty}{+\infty}=\frac{6}{\sqrt{9}}=\frac{6}{3}=\bm{2}$

지수 함수를 사용한 무한 사이의 무한 불확정성

마지막으로, 우리는 무한의 불확정성 지수의 사례만 연구하면 됩니다: 무한성과 지수 함수 사이의 무한 불확정성은 얼마나 됩니까?

지수 함수의 증가는 다항 함수의 증가보다 훨씬 크기 때문에 지수 함수의 차수는 다항 함수의 차수보다 크다는 점을 고려해야 합니다.

$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”> 그러므로, 무한 불확정성을 무한대로 나눈 것이 지수 함수의 극한에서 비롯된 경우 분자와 분모의 차수에 대해 설명된 동일한 규칙을 적용하는 것으로 충분하지만 지수 함수가 다항식보다 더 높은 차수라는 점을 고려하면 됩니다. . 또한 나눗셈의 분자와 분모에 지수 함수가 있는 경우 밑이 더 큰 지수 함수가 더 높은 차수가 됩니다. <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

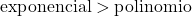
이 경우 분모는 지수함수로 구성되므로 분자보다 고차이다. 그러므로 무한 사이의 부정형 무한은 사라진다.

무한 사이의 무한 불확정 문제 해결

연습 1

다음 유리 함수의 극한을 계산합니다.

$\displaystyle\lim_{x \to +\infty} \cfrac{6x-5}{x^2-1}$

해결책 보기

극한을 계산할 때 무한대 사이의 무한 불확정성을 얻습니다. 그러나 분자의 차수가 분모의 차수보다 작으므로 불확정한 극한은 0과 같습니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{6x-5}{x^2-1} = \cfrac{6(+\infty)}{(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{0}$

연습 2

다음 불확정 극한을 해결합니다.

$\displaystyle\lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4}$

해결책 보기

극한을 계산하려고 시도하면 불확정성 무한대/무한대가 얻어집니다. 이 경우, 분자 다항식의 차수는 분모 다항식의 차수보다 크므로 부정한계는 플러스 무한대와 같습니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4} = \cfrac{(+\infty)^3}{5(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{+\infty}$

연습 3

무한대에서 다음 극한을 푼다:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

해결책 보기

극한은 플러스 무한대 사이에서 불확정성 마이너스 무한대를 제공합니다. 분자의 차수는 분모의 차수보다 크므로 부정한계는 플러스 무한대와 같습니다. 그러나 나눗셈은 양의 무한대로 음의 무한대이므로 결과는 음의 무한대가 됩니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

연습 4

다음 불확정 극한을 해결합니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

해결책 보기

이 문제에서 무한대에 대한 무한 불확정 형식은 동일한 차수의 두 다항식의 몫에서 얻어지므로 불확정 극한의 결과는 주요 계수의 나눗셈입니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

연습 5

다음 극한을 최소한 무한대로 계산합니다.

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

해결책 보기

분자의 대수적 표현의 차수는 분모의 표현의 차수보다 작으므로 불확정성 +무한대/+무한은 0을 제공합니다.

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

연습 6

근이 있는 함수의 다음 불확정 극한을 풉니다.

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

해결책 보기

분자 표현은 근호 아래에 있으므로 그 차수는 7/3입니다. 반면, 분모의 다항식은 2차입니다. 그리고 7/3>2이므로 극한은 플러스 무한대를 제공합니다.

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=+\infty$

연습 7

분수를 사용하여 다음 함수의 무한대 극한을 결정합니다.

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

해결책 보기

이 연습에서, 불확정성 마이너스 무한대를 마이너스 무한대로 나눈 값은 분모 차수보다 분자 차수가 더 큰 값으로 구해집니다. 따라서 다음과 같습니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

연습 8

다음 함수의 최소 무한대까지의 극한을 구합니다:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

해결책 보기

분모 다항식은 2차이고, 분자 다항식은 선형입니다. 따라서 불확정성의 무한대를 무한대로 나누면 0이 됩니다.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

연습 9

다음 함수의 최소 무한 극한을 푼다:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

해결책 보기

분자는 분모보다 차수가 더 크기 때문에 불확정 형식인 무한대/무한대의 결과는 무한대가 됩니다. 또한 양수를 음수로 나눈 값이 음수가 되기 때문에 무한대 기호는 음수가 됩니다.

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

연습 10

무한대 사이의 무한 불확정성을 사용하여 다음 극한을 해결합니다.

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

해결책 보기

지수 함수는 다항 함수보다 차수가 높으므로 극한은 무한대를 제공합니다. 그러나 양수를 음수로 나누면 무한대 기호는 음수가 됩니다.

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

연습 11

다음 한도를 계산합니다.

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2}$

해결책 보기

이 문제에서 무한대의 불확정성은 두 다항식의 주요 계수를 나눔으로써 해결됩니다. 두 다항식의 차수는 동일하기 때문입니다.

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2} = \cfrac{(-\infty)^3}{-(-\infty)^3} = \cfrac{-\infty}{-(-\infty)}= \cfrac{-\infty}{+\infty}=\cfrac{1}{-1}=\bm{-1}$

연습 12

x가 무한대에 접근할 때 다음 함수의 극한을 풉니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}$

해결책 보기

분자의 미지수는 직접 제곱되지 않지만, 주목할만한 항등식을 풀 때 분자의 차수가 분모의 차수보다 크다는 것을 분명히 알 수 있습니다. 아직:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}=\lim_{x \to +\infty} \cfrac{x^2+9+6x}{x} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

연습 13

세제곱근을 사용하여 다음 함수의 무한대 극한을 계산합니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}$

해결책 보기

분자는 세제곱근으로 구성되므로 차수는 3/3=1입니다. 그러면 분자의 차수는 분모의 차수와 같으므로 무한대 사이의 무한 불확정성은 다음과 같이 해결됩니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}= \cfrac{\sqrt[3]{8(+\infty)^3}}{-4(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt[3]{8}}{-4}=\cfrac{2}{-4}=\bm{-}\mathbf{\cfrac{1}{2}}$

연습 14

두 개의 근호를 사용하여 다음 함수의 무한대 극한을 푼다:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

해결책 보기

분자의 차수는 7/3 = 2.33이고 분모의 차수는 5/2 = 2.5입니다. 따라서 분자의 차수가 분모의 차수보다 작으므로 무한대 사이의 불확정 무한 극한은 0입니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

연습 15

다음 한도를 계산합니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

해결책 보기

분자의 차수에 관계없이 분모에 지수 함수가 있으므로 무한대에 대한 부정형 무한대 결과는 0입니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

무한 사이의 무한 불확정성을 해결하는 방법

분모의 차수보다 작은 분자의 차수

예시 1:

예 2:

분자의 차수는 분모의 차수와 같습니다.

예시 3:

예시 4:

분모의 차수보다 분자의 차수가 더 큽니다.

예시 5:

예시 6:

근과 무한 사이의 무한 불확정성

지수 함수를 사용한 무한 사이의 무한 불확정성

무한 사이의 무한 불확정 문제 해결

연습 1

연습 2

연습 3

연습 4

연습 5

연습 6

연습 7

연습 8

연습 9

연습 10

연습 11

연습 12

연습 13

연습 14

연습 15

댓글 달기 댓글 취소