좌표계

7월 11, 2023

이 페이지에서는 좌표계가 무엇인지 설명하고 또한 데카르트 좌표계에 대한 모든 것을 찾을 수 있습니다. 또한 다른 유형의 좌표계(극좌표, 원통형, 구형 등)와 좌표계의 실제 적용도 볼 수 있습니다.

좌표계란 무엇입니까?

처음에는 이 개념을 이해하기가 다소 어렵지만 좌표계의 정의는 다음과 같습니다.

좌표계는 점의 위치를 식별할 수 있는 시스템입니다. 즉, 기하학적 객체의 위치를 정의하는 데 사용되는 값 집합입니다.

예를 들어, 다음 비행기가 날아가고 있는 위치는 좌표계로 설명할 수 있습니다.

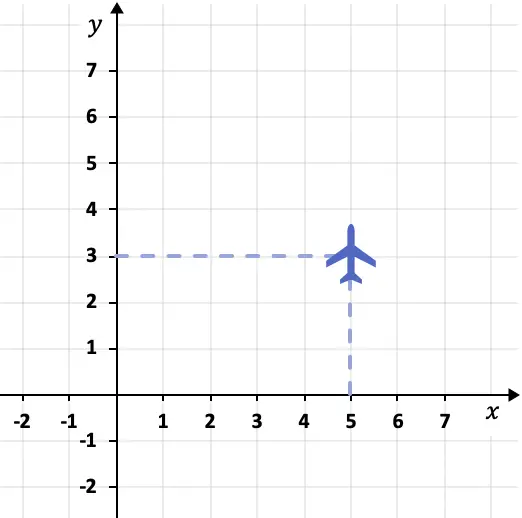
좌표계란 무엇인가

이 경우 평면은 지점 (5.3)에 있습니다. X 좌표가 5이고 Y 좌표가 3이기 때문입니다.

$(5,3)$

한편, 점 (0,0)은 좌표축이 시작되는 곳이자 좌표계의 기준점이므로 좌표 원점 이라고 합니다.

호기심에서 좌표계를 발명한 수학자 역시 프랑스인 르네 데카르트였던 것으로 추정된다. 이것이 바로 데카르트 좌표계라고도 불리는 이유입니다.

평면의 데카르트 좌표계

이전 섹션에서 본 그래프는 평면의 직교 좌표계에 속합니다. 2차원 시스템이기 때문에 평면에 있다고 말합니다. 즉 X축과 Y축이라는 두 개의 축만 있기 때문입니다.

X축은 가로 좌표를 나타내고 Y축은 세로 좌표를 나타냅니다. 아래에서는 좌표와 함께 그래픽으로 표현된 여러 점을 볼 수 있습니다.

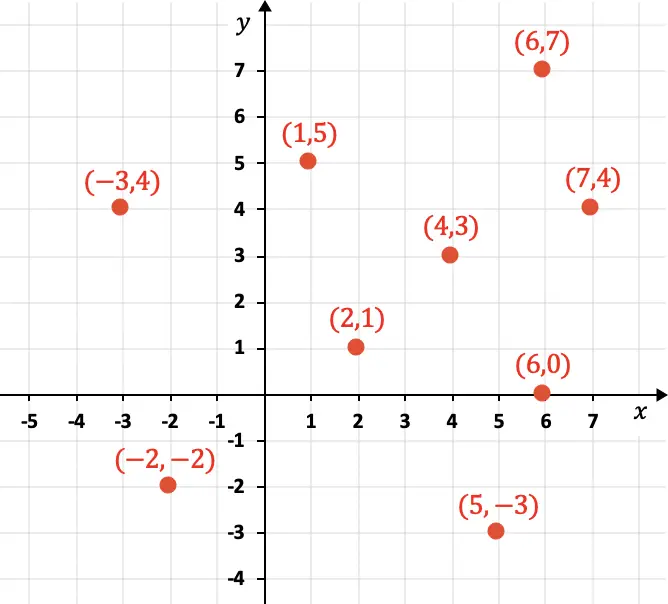
평면의 데카르트 좌표계

그래프에서 볼 수 있듯이 좌표는 괄호 안에 숫자로 표시되어 있으며, 추가적으로 X 구성 요소가 먼저 배치되고 Y 구성 요소가 다음으로 배치됩니다: (4,3). 또한 좌표는 양수, 음수 또는 0일 수 있습니다.

한편, 이러한 유형의 좌표계를 데카르트 평면이라고도 합니다.

마지막으로, 좌표축은 모두 같은 의미이지만 여러 가지 방식으로 말할 수 있다는 점을 알아야 합니다.

X축은 가로축 또는 OX축이라고도 합니다.
Y축은 y축 또는 OY축이라고도 합니다.

공간의 직교 좌표계

우리는 평면, 즉 두 개의 축(2차원)이 있는 좌표계에서 점을 표현하는 방법을 살펴보았습니다. 그러나 현실은 3차원(높이, 너비, 깊이)으로 구성됩니다.

따라서 유클리드 기하학에서 3차원 공간은 일반적으로 서로 수직인 세 개의 축을 가진 좌표계로 표현됩니다.

X축은 깊이를 나타냅니다.
Y축은 너비를 나타냅니다.
Z축은 높이에 해당합니다.

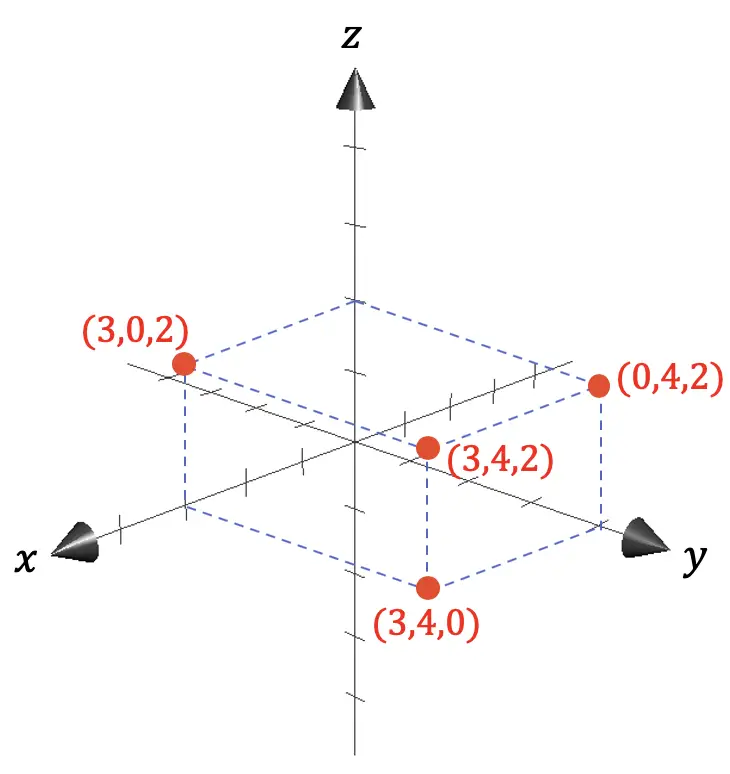
3D 공간의 직교 좌표계

이전 그래픽 표현에서 볼 수 있듯이 모든 점의 좌표는 해당 점과 원점(0,0,0) 사이의 거리 축에 대한 투영에 의해 제공됩니다.

극좌표계

2D 또는 3D 직교 좌표계가 가장 널리 사용됩니다. 그러나 어떤 경우에는 다른 유형의 좌표계를 사용하는 것이 편리할 수도 있습니다.

극좌표계는 좌표가 다음과 같은 2차원 참조 시스템입니다.

$\bm{r}$

좌표 원점과 점 사이의 거리입니다. 이것을 방사형 좌표라고 합니다.
$\bm{\theta}$

X축이 점과 원점을 통과하는 선과 이루는 각도입니다. 이를 각도 또는 방위각 좌표라고 합니다.

극좌표계

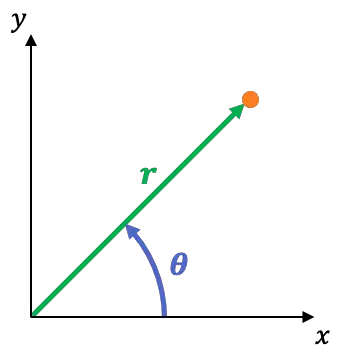
다음 방정식을 사용하여 직각 좌표계에서 극좌표계로 쉽게 전환할 수 있습니다.

극좌표를 데카르트 좌표로 변환

$x=r\cdot\text{cos}(\theta)$

$y=r\cdot\text{sen}(\theta)$

데카르트 좌표에서 극좌표로 전환

$r= \sqrt{x^2+y^2}$

$\displaystyle \theta = \text{arctan}\left(\frac{y}{x}\right)$

원통형 좌표계

원통형 좌표계는 극좌표계와 매우 유사합니다. 사실, 그것은 똑같지만 높이라는 좌표가 하나 더 있습니다.

따라서 원통형 프레임은 3차원 프레임, 즉 3개의 좌표를 갖는 프레임입니다.

$\bm{r}$

는 XY 평면에 있는 점의 직교 투영, 즉 Z축에서 점까지의 거리입니다.
$\bm{\theta}$

양의 반축이 이루는 각도

$r.$
$\bm{z}$

는 점의 높이이며 공간의 데카르트 좌표계와 동일한 좌표입니다.

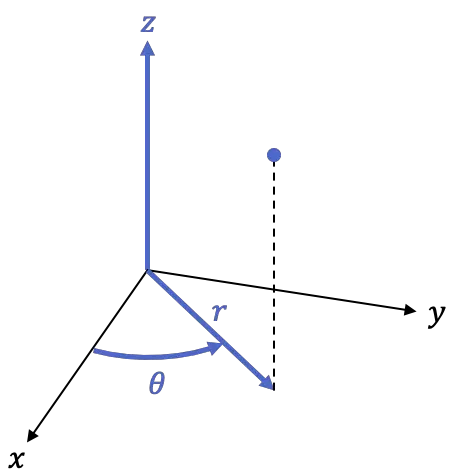
원통형 좌표계

다음 공식은 데카르트 좌표계를 원통형 좌표계로 변환하는 데 사용됩니다.

원통형 좌표를 데카르트 좌표로 변환

$x=r\cdot\text{cos}(\theta)$

$y=r\cdot\text{sen}(\theta)$

$z = z$

데카르트 좌표를 원통형 좌표로 변환

$r= \sqrt{x^2+y^2}$

$\displaystyle \theta = \text{arctan}\left(\frac{y}{x}\right)$

$z = z$

구형 좌표계

마지막으로 구면 좌표계가 있습니다. 이 유형의 좌표계는 극좌표 및 원통형 좌표계와도 매우 유사하지만 분명히 약간의 차이점이 있습니다.

구면 좌표계는 3차원 유클리드 공간을 설명하는 시스템이므로 다음과 같은 세 가지 좌표를 갖습니다.

$\bm{r}$

는 원점에서 점까지의 거리(R3)입니다.
$\bm{\theta}$

X축의 양의 부분이 선과 이루는 각도입니다.

$r$

XY 평면에 투영됩니다.
$\bm{\phi}$

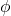
Z축의 양의 부분과 선 사이의 각도입니다.

$r.$

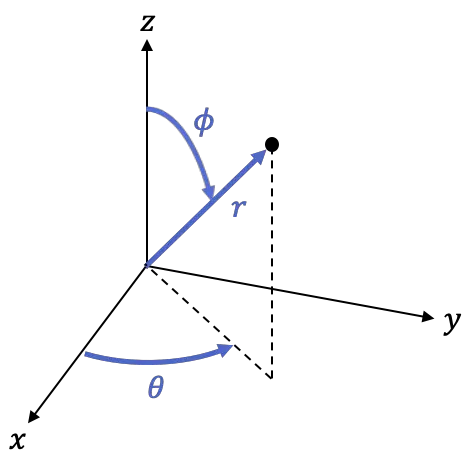
구형 좌표계

다음 공식을 사용하여 구면 좌표와 직교 좌표 간을 전환할 수 있습니다.

구면 좌표를 데카르트 좌표로 변환

$x=r\cdot\text{cos}(\theta)\cdot\text{sen}(\phi)$

$y=r\cdot \text{sen}(\theta)\cdot\text{sen}(\phi)$

$z = r\cdot\text{cos}(\phi)$

직교 좌표를 구면 좌표로 변환

$r= \sqrt{x^2+y^2+z^2}$

$\displaystyle \theta = \text{arctan}\left(\frac{y}{x}\right)$

$\displaystyle \phi = \text{arctan}\left(\frac{\sqrt{x^2+y^2}}{z}\right)$

좌표계의 실제 응용

좌표계는 실제 생활에서도 사용되기 때문에 수학에서 매우 중요합니다. 예를 들어, 지도에서 사물, 사람 또는 장소를 찾는 데 유용합니다. 실제로 GPS는 좌표계 때문에 존재합니다. 좌표계는 지구상에서 사용자의 위치를 아는 데 사용되기 때문입니다.

보다 정확하게는 GPS 지리 좌표는 위도와 경도라는 두 가지 요소로 구성됩니다. 위도(북쪽 또는 남쪽)와 경도(동쪽 또는 서쪽)는 지구 중심과 현재 위치 사이의 각도를 측정하는 두 개의 각도 좌표입니다. 둘 다 십진수 또는 60진수 좌표로 각도로 표시됩니다.

댓글 달기 댓글 취소