この記事では、2 つの関数から商 (または除算) を求める方法を説明します。関数の商の導関数の例があり、さらに、割り算の導関数について段階的な演習を行うことができます。
商の導関数の公式
関数の係数 (または除算) の導関数は、分母関数の導関数を高い分母関数の 2 乗で割った分子関数よりも小さい、分母関数による分子関数の導関数と同じです。

ご覧のとおり、商 (または割り算) の導関数にルールを適用すると、微分後も分数が残ります。ただし、分子には 2 つの乗算と 1 つの減算があり、分母は 2 乗されます。
商の導関数の例
2 つの関数の商の導関数の公式を説明しました。次に、このタイプの演算の導関数の例をいくつか解いていきます。関数商の導出方法がわからない場合は、コメントセクションで質問してください。
例1
この例では、三角関数で割ったポテンシャル関数を導出します。
![]()
2 つの異なる関数の除算の導関数の公式は次のとおりです。
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
したがって、最初に各関数の導関数を個別に計算する必要があります。
![]()
![]()
したがって、関数全体の導関数は次のようになります。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-65ce4673f3ad5a4c09a9b2e7c611821d_l3.png)
例 2
この場合、定数を関数で割った導関数を求めます。
![]()
上で見たように、2 つの異なる関数の除算の導関数のルールは次のとおりです。
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
したがって、分子と分母の導関数を別々に計算します。
![]()
![]()
そして最後に、整数の除算の導関数を求めます。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f8bdea77dc91b1aff40695511593e86_l3.png)
実際、分子に定数を関数で割った場合、定数の導関数は常に 0 になるため、直接微分する公式を導出できます。したがって、次の公式は常に true になります。
![]()
例 3
この演習では、2 つの多項式の商を導出します。
![]()
導関数を解くには、次のような 2 つの異なる関数の商の導関数のルールを適用する必要があります。
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
ここで、分子多項式と分母多項式の導関数を求めてみましょう。
![]()
![]()
したがって、多義語の除算の導関数は次のようになります。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-065ad49556f264b4cfb505522ad7566b_l3.png)
最後に、演算を実行して、可能な限り分数を単純化します。
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-af3f7cb513883d1fa5dadca23701c19d_l3.png)
商の微分に関する演習を解決しました
次の関数の分割を導き出します。
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-26b0af84dd46ca29727eee97380b4ca4_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-11f9c8fda61edb1ce51bd33e022a0a24_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ec87daa1a463bacd5a42a1b16e826449_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef2b22482e39cea7e82047c0d9911b0_l3.png)
商の導関数のデモンストレーション
最後に、除算の導関数の公式を示します。これを行うには、次のような導関数の一般的な定義を使用します。
![]()
z を2 つの異なる関数の除算とします。
![]()
次に、数学的定義を適用した関数zの導関数は次のようになります。
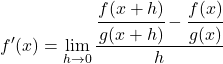
分数の分子から分数の引き算を解きます。
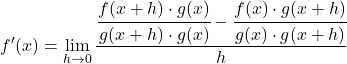
![]()
方程式に加算項と減算項を追加しても、方程式は変わりません。したがって、次のステップに進むことができます。
![]()
共通因数を抽出します。
![]()
ここで、分数の性質を使用して項hを分母から分子に移動してみましょう。
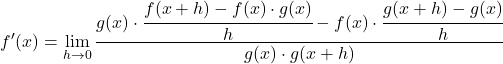
限界の特性を適用して方程式を変形します。
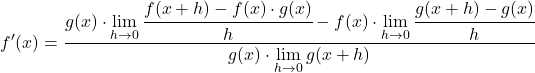
分子の極限は、各関数の導関数の数学的定義に正確に対応します。したがって、次のようになります。
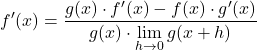
分数の分母の極限を解きます。
![]()
したがって、2 つの関数の商の導関数の公式が示されます。
![]()