このページでは、関数とデカルト軸の交点 (または交差) とは何か、およびその計算方法について説明します。さらに、それらがどのように見つけられるかを完全に理解するためのいくつかの例があり、段階的に解決された演習で練習することもできます。
関数と軸の交点 (または交点) は何ですか?
計算方法を確認する前に、関数と軸の交点が何であるかを覚えておきましょう。
交差または軸の交点は、関数の表現が座標軸と交差する点、つまり X 軸と l 軸を結ぶグラフ上の点です。 Y軸。
たとえば、次のグラフの放物線は点 (0,3) で Y 軸と交差し、点 (-1,0) および (3,0) で X 軸と交差します。
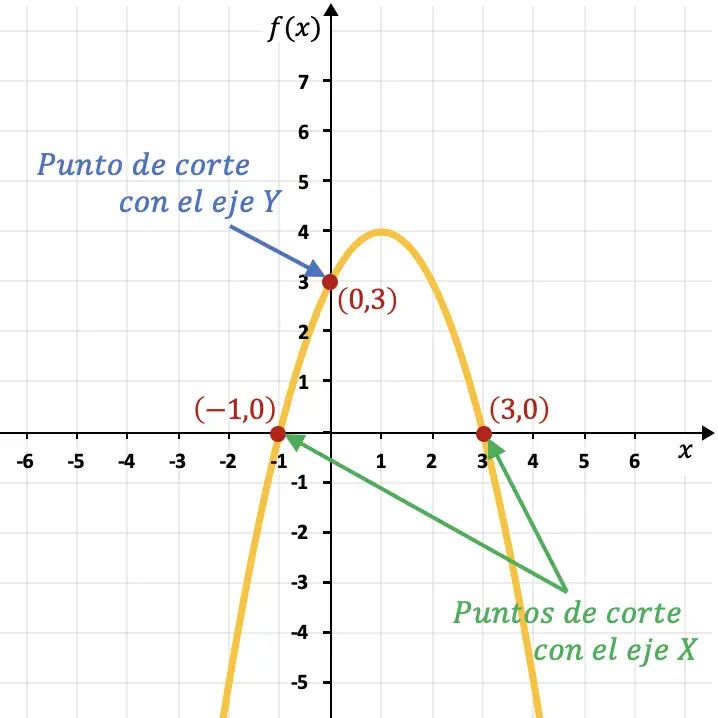
X軸による関数のカットポイント
したがって、関数と X 軸の交点の 2 番目の座標は常に 0 になります。
任意の x 軸関数 OX のカットオフ点は次の形式になります。
![]()
であり、次の方程式を解くことで計算できます。
![]()
この方程式を解くときに、2 つ (またはそれ以上) の解が得られることがあります。これは、関数が X 軸と 2 回 (またはそれ以上) 交差することを意味します。一方、方程式に解がない場合は、関数が X 軸と交差していないことを意味します。
Y軸による関数のカットポイント
したがって、関数と Y 軸の交点の最初の座標は常に 0 になります。
y 軸 OY を持つ関数のカットオフ点は次の形式になります。
![]()
、そして x=0 での関数のイメージを計算することで見つけることができます。
![]()
X 軸上のブレークポイントとは異なり、Y 軸上のブレークポイントは 1 つだけです。
軸を使用した関数のカットオフ点を計算する例
疑いのないように、デカルト軸を使用して関数のカットポイントを見つける方法の例を以下に示します。
- 次の関数のカットオフ点を数値的に求めます。
![]()
まず、x 軸を使用して関数のカットオフ ポイントを計算します。 X 軸との交点は常に 0 に等しい 2 番目のコンポーネントを持ちます。つまり、次のタイプになります。
![]()
。 f(x) は OX 軸上で常に 0 に等しいためです。したがって、点の他の成分を見つけるには、方程式を解く必要があります。
![]()
![]()
![]()
![]()
![]()
したがって、X 軸との交点は次のようになります。
![]()
次に、y 軸との交点を見つけます。 Y 軸との交点は常に 0 に等しい最初のコンポーネントを持ちます。つまり、点は次のタイプになります。
![]()
。独立変数xは常に Y 軸上でキャンセルされるため。したがって、点の他の座標を見つけるには、計算する必要があります
![]()
![]()
したがって、Y 軸との交点は次のようになります。
![]()
以下に関数の例をグラフで示します。見つかったしきい値がグラフ内のしきい値と一致していることがわかります。
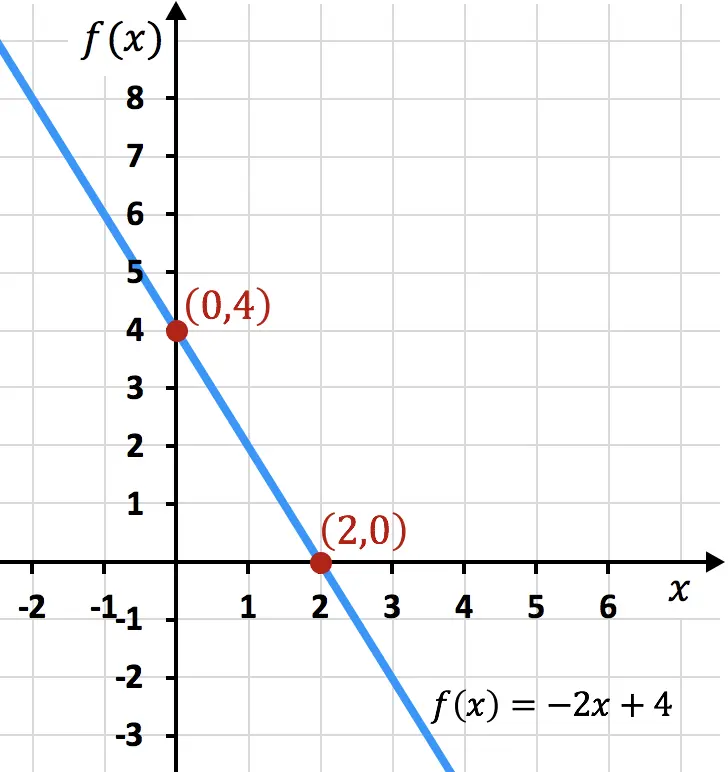
軸のある関数のカットポイントに関する演習を解決しました
演習 1
次の関数の座標軸を使用して切断点を決定します。
![]()
X軸を伴う切断点
関数と X 軸の交点を見つけるには、次を解く必要があります。
![]()
![]()
![]()
![]()
![]()
したがって、関数と X 軸の交点は次のようになります。
![]()
Y軸を伴う切断点
Y 軸との交点を見つけるには、計算する必要があります。
![]()
![]()
したがって、関数と Y 軸の交点は次のようになります。
![]()
演習 2
次のアフィン関数のデカルト軸との交点を見つけます。
![]()
X軸を伴う切断点
OX 軸を使用した関数の限界点を見つけるには、関数をゼロに設定し、結果として得られる方程式を解く必要があります。
![]()
![]()
![]()
![]()
したがって、関数と横軸の交点は次のようになります。
![]()
Y軸を伴う切断点
OY 軸でカットオフ ポイントを見つけるには、次のように計算する必要があります。
![]()
![]()
したがって、関数とコンピューター軸の交点は次のようになります。
![]()
演習 3
次の二次関数の軸を使用してカットオフ ポイントを計算します。
![]()
X軸を伴う切断点
関数と X 軸の交点を見つけるには、次を解く必要があります。
![]()
![]()
![]()
この場合、二次方程式を解く必要があるため、次の公式を適用します。
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-47048fdd48ce98ba99629edf5a379f76_l3.png)
二次方程式の 2 つの解が得られたため、関数は 2 つの点で X 軸と交差します。
![]()
Y軸を伴う切断点
一方、Y軸との交点を求めるには、次のように計算する必要があります。
![]()
![]()
したがって、関数と Y 軸の唯一の交点は次のとおりです。
![]()
演習 4
次の有理関数のデカルト平面の軸との交点を見つけます。
![]()
X軸を伴う切断点
関数と X 軸の交点を見つけるには、次を解く必要があります。
![]()
![]()
![]()
![]()
![]()
![]()
5 は 0 と等価ではないため、方程式には解がなく、したがって関数と X 軸の間に交点はありません。
Y軸を伴う切断点
Y 軸との交点を見つけるには、計算する必要があります。
![]()
![]()
ゼロで割った数値は無限大を与える不確定性です。したがって、関数はどの点でも Y 軸を越えることはありません。
つまり、運動関数には軸との交点がありません。つまり、そのグラフはどの点でも X 軸または Y 軸を通過しません。
演習 5
次の 3 次関数の軸を使用してカットオフ ポイントを計算します。
![]()
X軸を伴う切断点
関数と X 軸の交点を見つけるには、次を解く必要があります。
![]()
![]()
![]()
方程式の両方の項にはxがあり、これを使用して共通因数を抽出できます。
![]()
前述の等式が満たされるには、因子の 1 つが 0 でなければなりません。したがって、考えられるすべての解を取得するには、各因子を 0 に設定します。
![Rendered by QuickLaTeX.com \displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-37febaed85a502533604305b9009611d_l3.png)
したがって、3 次方程式の 3 つの解が得られたため、関数は X 軸を 3 つの点で切断します。
![]()
Y軸を伴う切断点
Y 軸でカットポイントを計算するには、次のように計算する必要があります。
![]()
![]()
したがって、関数と Y 軸の唯一の交点は座標原点 (0,0) です。
![]()
この関数は両方の軸で同時にこの点をカットするため、X 軸でのカット点の計算でこの点がすでに見つかっていることに注意してください。