▷ 関数が連続かどうかを知る方法 (解決された演習)

この記事では、連続関数とは何か、および関数がある点で連続であるかどうかを判断する方法について説明します。さらに、連続関数のプロパティと最も一般的な関数の連続性解析も見つかります。最後に、連続関数に関する解決済みの演習を使って練習し、概念を完全に理解することができます。

連続関数とは何ですか?

関数の連続性をグラフで調べることができます。連続関数とは、紙から鉛筆を落とさなくてもグラフ上に表現できる関数です。

連続機能

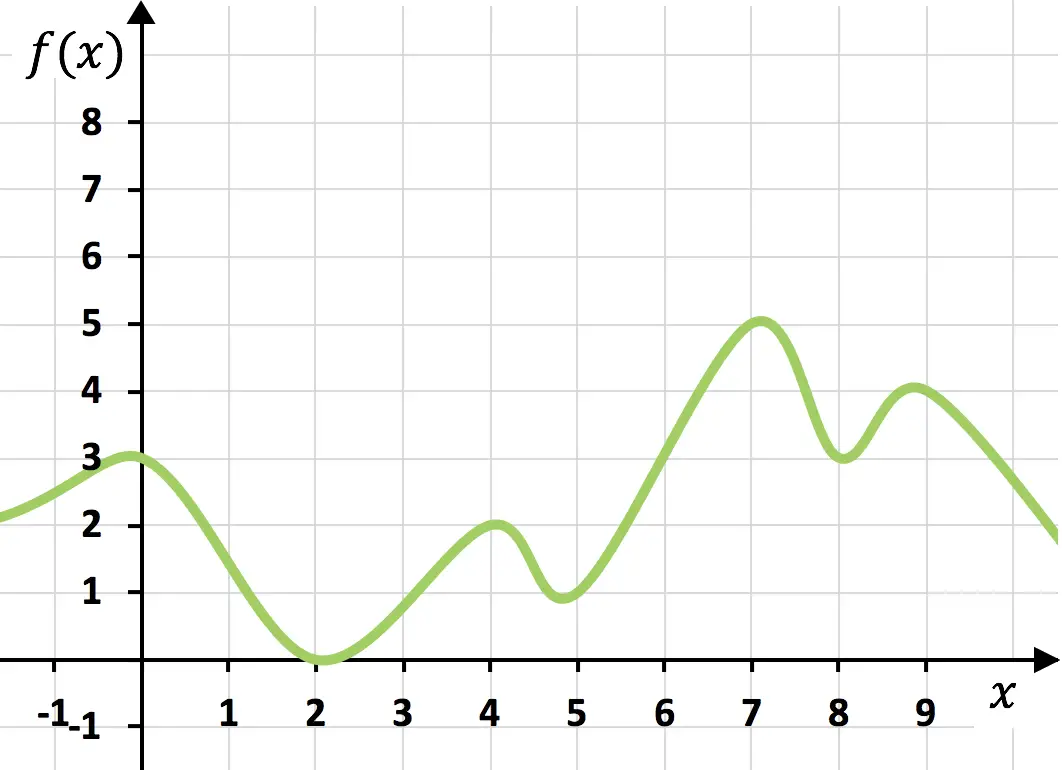
上記の機能は、紙から手を離さずに一筆書きできるため連続的です。

逆に、関数の中に前の連続条件が入っていない場合、その関数は不連続関数と言われます。

不連続関数

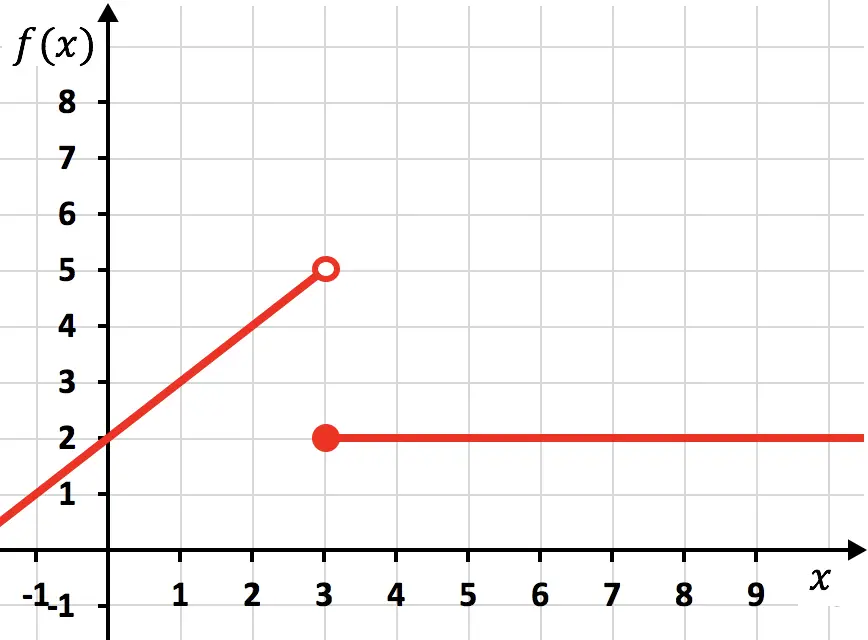
前の関数は、それを表すために鉛筆で 2 本の線を引く必要があるため、不連続です。この場合、関数は x=3 で連続でなくなります。したがって、x=3 は不連続点であると言います。

また、不連続には、回避可能な不連続、不可避の有限ジャンプ不連続、不可避の無限ジャンプ不連続の 3 種類があります。次のリンクでは、各タイプの不連続性がどのようなものであるか、またそれぞれの違いは何かを確認できます。

➤参照:不連続性の種類

ある点における関数の連続性

連続関数のグラフがどのように見えるかを確認したら、関数が連続かどうかを分析的に判断する方法を見ていきます。

数学的には、次の 3 つの条件が満たされる場合、関数はある点で連続です。

この点に関数が存在する、つまり点のイメージが存在する。

$\exists \ f(a)$

この時点では機能の限界があります。したがって、この時点での関数の左右の横方向の限界は等しくなります。

$\displaystyle \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \quad \color{orange}\bm{\longrightarrow}\color{black} \quad \exists \lim_{x \to a} f(x)$

点のイメージは、この点での関数の限界と一致します。

$\displaystyle f(a)=\lim_{x \to a} f(x)$

したがって、関数のすべての点で 3 つの連続条件が満たされる場合、その関数は連続です。

例として、次の区分関数の連続性を分析します。

セクションを変えてもその時点で

$x=-2$

この点での関数の横方向の限界は等しく、この点での関数の値と一致するため、関数は連続的です。

$\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3$

一方、関数は次の点では連続ではありません。

$x=4$

2 つの横方向の制限が異なるため、この時点では関数の制限は存在しません。

$\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2$

つまり、ピースによって定義される関数は、実数を除くすべての実数において連続です。

$x=4,$

断絶があるところ。

また、関数が不連続であることも確認できます。

$x=4$

それをグラフィカルに表現するには、この時点で紙から鉛筆を取り除く必要があるからです。

初等関数の連続性

特定の種類の関数は、その特性により連続的です。

定数関数はすべての実数において連続です。

$f(x)=k$

多項式関数はすべての実数に対して連続です。

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

有理（または分数）関数は、分数の分母を打ち消す値を除いてすべての実数で連続しており、これらの点で関数は不連続性を示します。

$f(x)=\cfrac{p(x)}{q(x)}$

指数関数はすべての実数にわたって連続です。

$f(x)=a^x$

対数関数は、引数を正にするすべての点で連続です。

$f(x)=\log_a (x)$

無理関数、またはルートを持つ関数の連続性は、根号 (n) のインデックスに依存します。インデックスが偶数の場合、これらはルート引数を 0 以上にするすべての点での連続関数です。しかし、インデックスが奇数の場合、それらはすべての実数に対する連続関数になります。

$f(x)=\sqrt[n]{x}$

三角関数の連続性は関数の種類によって異なります。サイン関数とコサイン関数は実数の集合にわたって連続ですが、タンジェント関数は点で不連続です。
$\displaystyle x=\frac{\pi}{2}+k\pi$

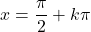
( kは整数です)。

$f(x)=sen(x)\qquad f(x)=cos(x)\qquad f(x)=tg(x)$

連続関数の性質

ショーン

$f(x)$

そして

$g(x)$

点における 2 つの連続関数

$x=a,$

次：

ある点における2 つの連続関数の合計は、その点における別の連続関数になります。

$f(x)+g(x)$

ある点における2 つの連続関数の積は、その点における別の連続関数と等しくなります。

$f(x)\cdot g(x)$

ある点で2 つの連続関数を除算すると、その点で除算関数がキャンセルされない限り、その点で別の連続関数が生成されます。

$\cfrac{f(x)}{g(x)}\qquad g(a)\neq 0$

ある点で2 つの連続関数を合成すると、同じ点で 1 つの連続関数が生じます。

$f(x)\circ g(x)$

➤ 「複合関数とは何ですか?」を参照してください。

関数の連続性に関する解決された演習

演習 1

次のグラフに示されている関数の不連続点を見つけます。また、それがどのようなタイプの不連続であるかを判断します。

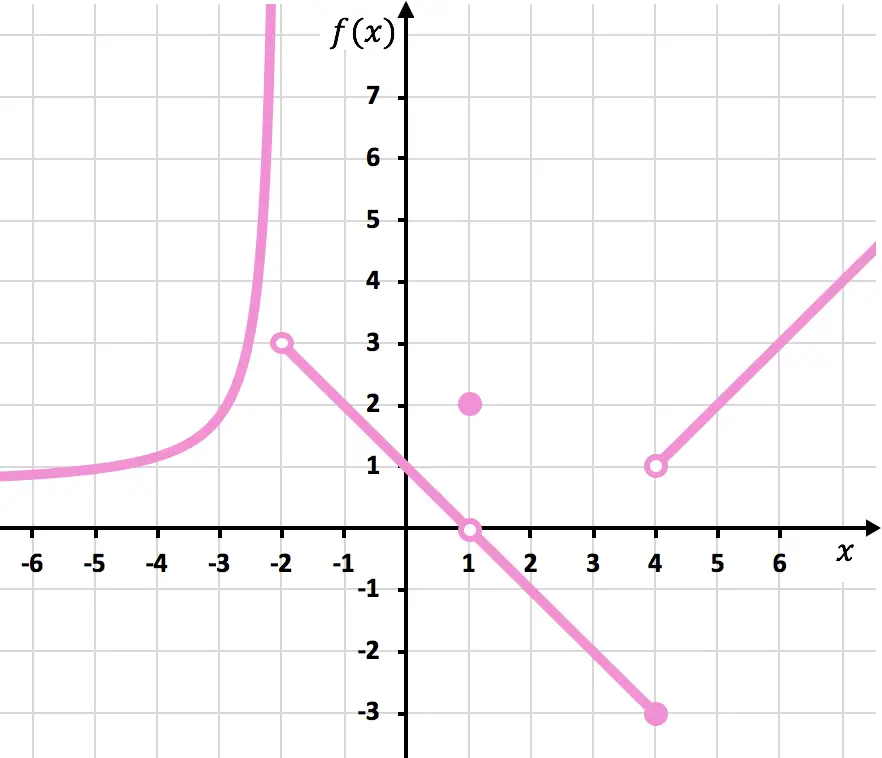
注:この演習を実行するには、まずさまざまな種類の不連続性が何であるか、またそれらがどのように識別されるかを確認することをお勧めします。不連続タイプの原理のリンクで説明を参照できます。

解決策を見る

関数を描くには、x=-2、x=1、x=4 の位置で鉛筆を持ち上げる必要があります。したがって、関数はこれら 3 つの点で不連続になります。

x=-2 では、左側の限界は +∞ で、右側の限界は 3 です。したがって、辺の限界の 1 つが無限であるため、関数には x=-2 で無限ジャンプの不連続性が避けられません。

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

x=1 での関数の限界は 0 であり、一方、x=1 での関数の値は 2 に等しい。したがって、この関数は x=1 で回避可能な不連続性を示します。

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(0) = 2$

x = 4 では、左側の限界は -3 で、右側の限界は 1 です。したがって、2 つの辺の限界は異なり、どちらも無限大を与えないため、関数には必然的に x =4 で有限ジャンプの不連続性が生じます。

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

演習 2

次のグラフに示されている関数が不連続になる点を特定します。

解決策を見る

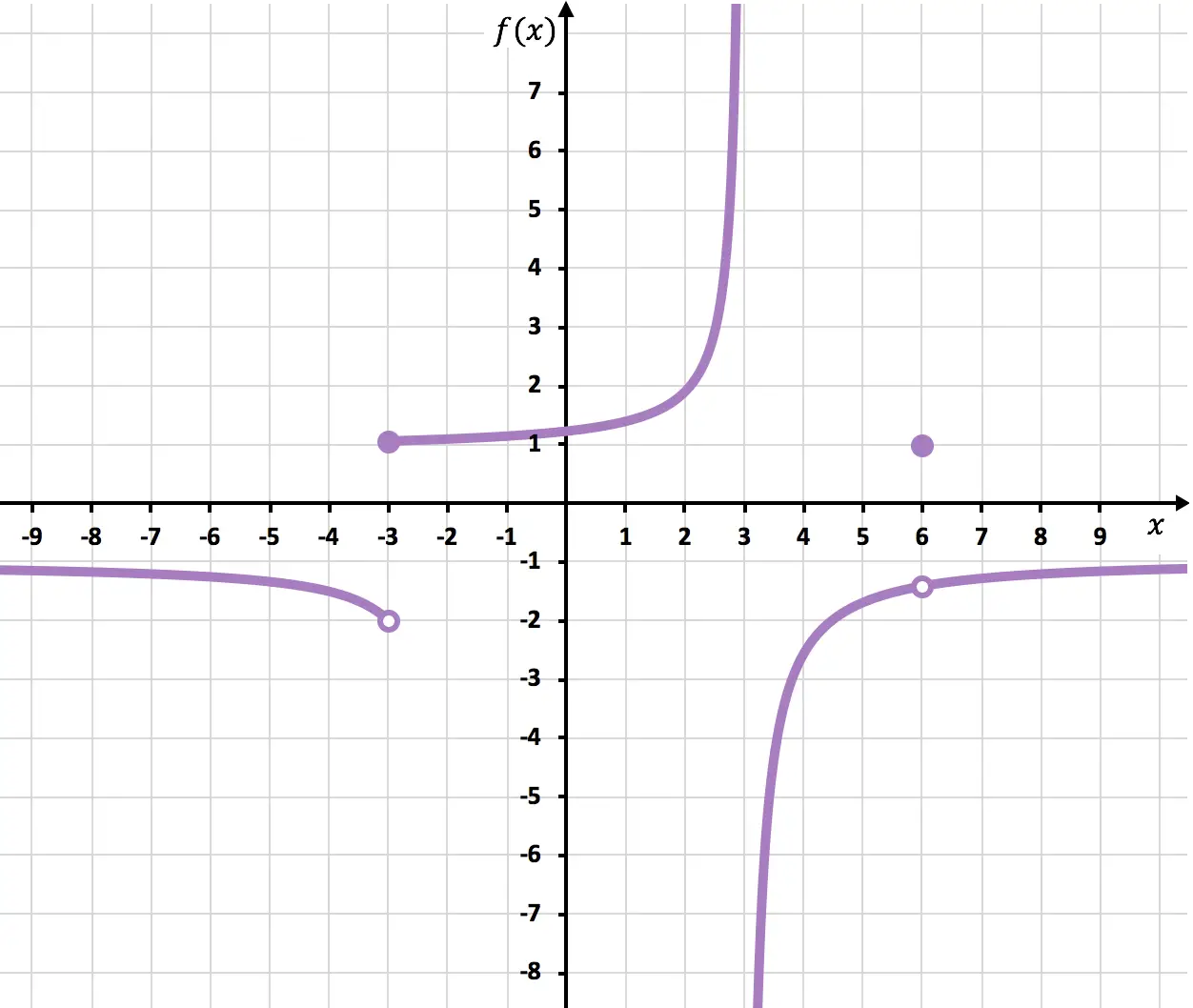
点 x=6 では、開いた点があるため、関数は中断されます。 x が 6 に近づくときの限界は -1.4 ですが、f(6)=1 になります。したがって、制限の値が関数の値と一致しないため、関数には x=6 で回避可能な不連続性があります。

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

x=-3 では、横方向の限界は一致せず、どれも無限大を与えません。したがって、関数には x=-3 で有限ジャンプの不連続性が避けられません。

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

そして最後に、この時点で少なくとも 1 つの横方向の限界が無限大になるため、この関数には x = 3 で無限ジャンプの不連続性が避けられません。

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

演習 3

次の有理関数の連続性を分析します。

$\displaystyle f(x)= \frac{2}{x-5}$

解決策を見る

有理関数はその領域全体、つまり分母を打ち消す値を除くすべての実数において連続です。したがって、どの点がドメインに属していないのかを確認するために、有理関数の分母をゼロに設定します。

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

したがって、関数は x=5 を除くすべての点で連続になります。

演習 4

次の区分関数の連続性を分析します。

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.$

解決策を見る

最初のセクションでも関数は連続しています。

$5x-2$

、2番目のセクションと同様に、

$x^2+2$

、これらは多項式関数であるためです。

したがって、関数が不連続である可能性がある唯一の点は、関数が区分的に分割される点です。この時点での横方向の制限を計算しましょう。

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1} (5x-2)=5\cdot 1-2=\bm{3}$

$\displaystyle \lim_{x \to 1^+} f(x) = \lim_{x \to 1} (x^2+2)=1^2+2=\bm{3}$

したがって、2 つの横方向の限界は一致し、x が 1 になる傾向があるときの関数の限界は 3 に等しくなります。

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 3 \ \bm{\longrightarrow} \ \exists \lim_{x \to 1} f(x) = 3$

さらに、x=1 の画像も 3 になります。

$f(1)=1^2+2=\bm{3}$

したがって、x=1 での関数の極限は前記点の画像に等しいため、関数は点 x=1 で連続です。したがって、それはすべての実数において連続です。

$\displaystyle f(1)=\lim_{x \to 1} f(x)$

演習 5

次の無理関数の連続性を調べてください。

$f(x)=\sqrt{2x+6}$

解決策を見る

これは偶数のインデックスを持つ根号関数であるため、根号の引数が 0 より大きい限り、関数は連続的になります (負の数の平方根は存在しないため)。

$2x+6\ge 0$

不等式を解きます。

$2x\ge -6$

$x\ge \cfrac{-6}{2}$

$x\ge -3$

解は、-3 以上のすべての数値で構成されます。したがって、関数はその定義域の区間で連続です。

$\mathbf{Dom } \ \bm{f = [-3,+\infty) }$

演習 6

次の対数関数の連続性を解析します。

$f(x)=\log_3 (-3x+6)$

解決策を見る

これは対数関数であり、負の数の対数も 0 の対数も存在しません。したがって、この関数は、対数の引数が正 (ゼロより大きい) である限り存在します。

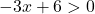$-3x+6>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ 不等式を解きます。

$-3x>-6″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”78″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{-6}{-3}$

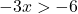
負の数を不等式の反対側で割るときは、不等式の符号を反転する必要があることに注意してください。

$x<2$

解は 2 未満のすべての数値で構成されます。したがって、関数の定義域は次のようになります。

$\mathbf{Dom } \ \bm{f = (-\infty,2) }$

したがって、関数はその領域内のすべての点で連続的です。

演習 7

次の関数の連続性を計算します。

$f(x)=\cfrac{4x-2}{\sqrt{-2x-8}}$

解決策を見る

分数の分母には偶数のインデックスを持つ根号があるため、根の内容が 0 以上である場合は常に関数が存在します。

$-2x-8\geq 0$

ただし、根は分数の分母にあり、分数の分母は決して 0 になることはありません。したがって、関数は根の内容が厳密に 0 より大きい場合にのみ存在します。

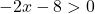$-2x-8> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ ここで不等式を解きます。

$-2x>8″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”64″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{8}{-2}$

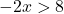
不等式を乗算または除算して負の数の辺を変更するときは、不等号も回転する必要があることに注意してください。

$x<-4$

結果はすべて -4 未満の数値になります。したがって、関数の定義域、したがってその連続性は、次の間隔によって定義されます。

$\mathbf{Dom } \ \bm{f = (-\infty,-4) }$

演習 8

関数が全体にわたって連続となるようにkの値を計算します。

$\mathbb{R} .$

$\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”225″ style=”vertical-align: 0px;”> <div class=$