この記事では、逆関数 (または逆関数) とは何か、および関数の逆関数を計算する方法について説明します。また、関数に逆関数があるかどうかを簡単に知る方法と、このタイプの関数のプロパティについても説明します。最後に、逆関数に関する段階的な演習で練習することができます。
逆関数とは何ですか?
逆関数は、逆関数とも呼ばれ、その定義域が別の関数 (元の関数) の範囲であり、その範囲が元の関数の定義域である関数です。関数fの逆関数は記号f -1で表される。
したがって、 f(x)の逆関数は、次の条件を満たす関数になります。
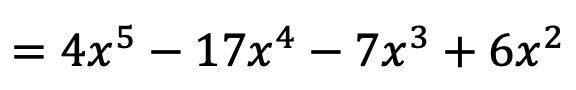
金
![]()
はの逆関数です
![]()
逆関数の概念は、関数合成を使用して定義することもできます。これは、逆関数で合成された関数は恒等関数と等しいためです。
![]()
➤ 「関数合成とは何ですか?」を参照してください。
したがって、前の式が満たされる場合、それは次のことを意味します。
![]()
は、の逆関数 (または逆関数) です。
![]()
逆関数の例
逆関数の定義を踏まえて、その意味をより深く理解するために例を解いてみましょう。
- 次の関数が互いに逆関数であるかどうかを判断します。
![]()
2 つの関数が互いに逆関数である場合、次の 2 つの条件が満たされます。
![]()
それでは、両方の方程式が満たされるかどうかを確認してみましょう。まず確認します
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36f7d5f4d815a58f808114ae471c31dd_l3.png)
➤ 先ほど行った計算が理解できない場合は、上のリンク「関数の構成とは何ですか?」にアクセスする必要があります。では、このような操作を関数で解決する方法を説明します。
となることによって
![]()
はい、達成されました。 ✅
今度は等価性を確認しましょう
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83423fe7deab472f1a7e9575ec7af8c4_l3.png)
そして可逆条件
![]()
それも達成されています。 ✅
結論として、両方の方程式が成り立つように、 2 つの関数は互いに逆関数です。
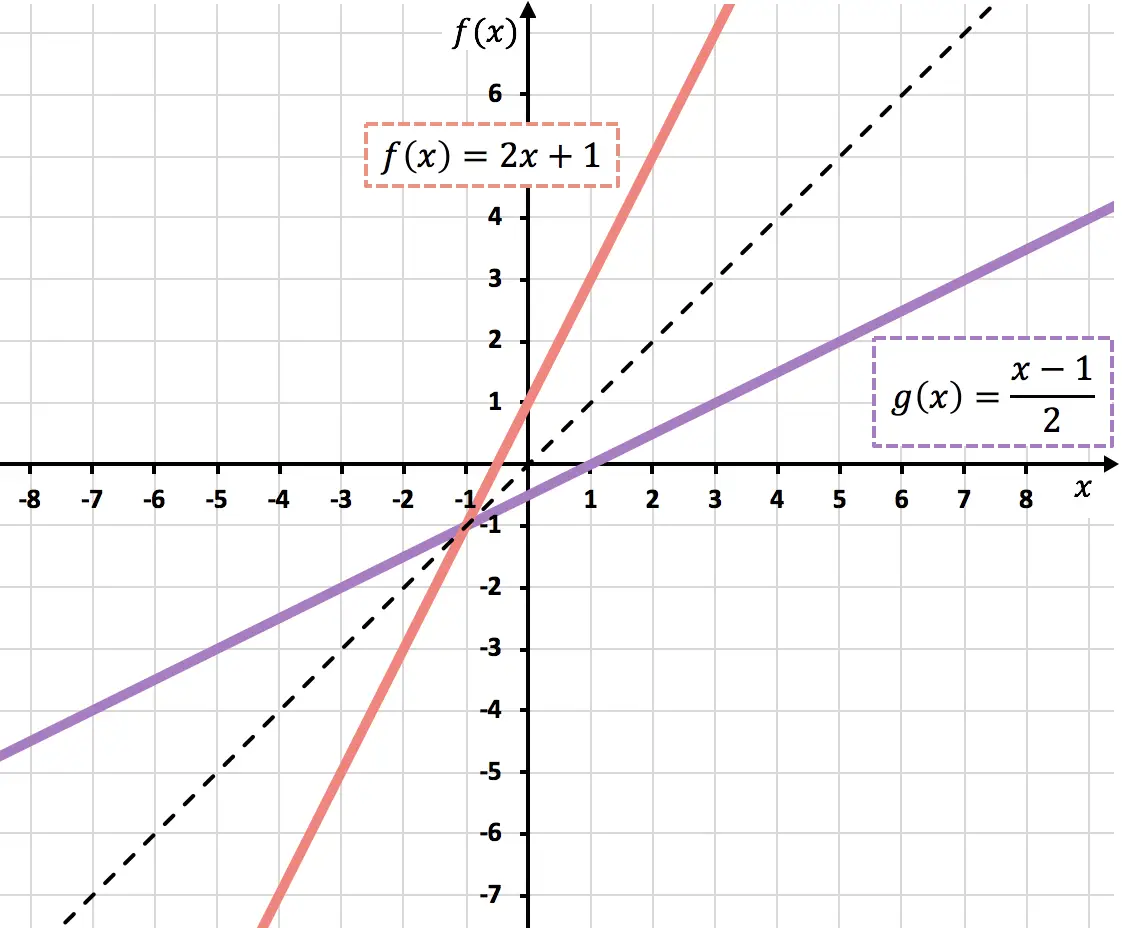
以下に、両方の関数をグラフ化して示します。 2 つの逆関数のグラフは、第 1 象限と第 3 象限の二等分線に関して対称であることに注意してください。
関数に逆関数があるかどうかを確認する方法
関数が単射関数である場合、つまり領域全体の各値が区間内の 1 つの値に対応する場合、関数は逆関数を持ちます。
逆関数を伴う指数関数

逆関数のない二次関数

たとえば、左の指数関数は、各x がf(x)の単一の値に対応するため、逆関数になります。一方、右二次関数には、画像が等しいxの値がいくつかあるため、逆関数はありません (たとえば、 f(1)=f(3)=2) 。
同様に、全単射関数は単射関数と全単射関数の両方から構成されているため、全単射関数には逆関数もあります。
一方、逆関数は関数の乗法逆関数と同じものではなく、2 つの異なる概念であることに留意する必要があります。関数の逆乗を求めるには、その関数によって単純に 1 つの対応関係を計算します。
![]()
次のセクションでは、逆関数を決定する方法を見ていきます。
逆関数の求め方
関数の逆関数を計算するには、次の手順を実行する必要があります。
- f(x)をyに置き換えます。
- すべてのxをyに変更し、その逆も同様です。
- y変数をクリアします。
- 変数y をf -1 (x)に置き換えます。逆関数は、 f -1 (x)で見つかった式です。
逆関数がどのように計算されるかを正確に理解できるように、例として次の関数の逆関数を決定します。
![]()
まず第一に、交換する必要があります
![]()
のために
![]()
:
![]()
今、私たちはすべてを変えます
![]()
による関数の
![]()
、 およびその逆:
![]()
次に変数をクリアします
![]()
![]()
![]()
![]()
![]()
そして最後に、の逆関数
![]()
を分離することによって得られた代数式です。
![]()
![]()
逆関数の演習問題を解いた
以下に、逆関数に関する段階的な演習をいくつか用意しましたので、練習していただけます。
👉 演習の解き方がわからない場合、または私たちに問題を解決してほしい場合は、コメント欄に書いてください。
演習 1
次の 2 つの関数が逆関数 (または逆関数) であるかどうかを確認します。
![]()
2 つの関数が互いに逆関数になるには、次の条件が満たされる必要があります。
![]()
したがって、2 つの条件が満たされているかどうかを確認する必要があります。まず確認します
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fbbdf5bb2c308a1973c5f2d99e822ad5_l3.png)
まだ、
![]()
はい、達成されました。 ✅
他の関数構成を確認してみましょう
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5819584c8358b812c8214a902e4f08_l3.png)
それによって
![]()
それも達成されています。 ✅
それはどうやって起こるのですか
![]()
そして
![]()
、2 つの関数は互いに逆関数です。
演習 2
次の 1 次多項式関数の逆関数 (または逆関数) を計算します。
![]()
関数を逆にするために最初に行うことは、次の項を置き換えることです。
![]()
のために
![]()
![]()
ここで、
![]()
による
![]()
、 およびその逆:
![]()
そしてリリースします
![]()
![]()
![]()
![]()
![]()
すでにリリースに成功しています
![]()
。したがって、の逆関数は、
![]()
東:
![]()
演習 3
次の二次多項式関数を反転します。
![]()
逆関数を見つけるには、上で見た手順に従います。それで、私たちは電話します
![]()
関数に
![]()
![]()
次に、
![]()
のために
![]()
、 およびその逆:
![]()
そして最後に変数を分離します
![]()
![]()
![]()
![]()
![]()
ただし、この場合、得られる関数には、その領域の要素ごとに 2 つのイメージ (ポジティブ イメージとネガティブ イメージ) が含まれます。したがって、問題関数の逆関数は存在しません。
演習 4
次の有理関数の逆関数 (または逆関数) を求めます。
![]()
まず、交換します
![]()
のために
![]()
![]()
ここで、
![]()
分子と分母
![]()
、 およびその逆:
![]()
そしてリリースします
![]()
![]()
表現
![]()
は方程式の右側全体を除算するので、方程式の左側全体を乗算することで乗算できます。
![]()
![]()
すべての条件を以下に示します
![]()
方程式の一方の側に、他の項がもう一方の側にあります。
![]()
クリアするには
![]()
、方程式の左側から共通因数を抽出します。
![]()
そして郵便配達員として
![]()
方程式の左側全体を乗算することですが、右側全体を除算することでこれを行うことができます。
![]()
すでにリリースに成功しています
![]()
。したがって、の逆関数は、
![]()
東:
![]()
逆関数の性質
逆関数には次のような特徴があります。
- 逆関数は一意です。つまり、関数が可逆である場合、この関数には逆関数が 1 つだけ存在します。
- 逆関数の定義域は、元の関数の範囲 (または範囲) です。
- 同様に、逆関数のパスは元の関数のドメインに相当します。
- 逆関数で構成される関数は恒等関数 (x) を与えます。
![]()
- 関数のグラフとその逆関数のグラフは、第 1 象限と第 3 象限の二等分線に関して対称です。
- 逆関数の逆関数は元の関数と同じです。
![]()
- 複合関数の逆変換は、各関数の逆関数を個別に計算して、逆関数を合成することと同じです。
![]()
- 関数はその逆関数と同時に連続です。つまり、関数が連続であれば、その逆関数も連続です。
- 関数が微分可能であり、導関数がいつでも消滅しない場合
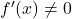
、その逆関数も微分可能です。
さらに、逆関数の導関数は、逆関数定理を適用することで計算できます。その式は次のとおりです。
![]()