▷ 逆正接の導関数（公式と例）

この記事では、関数の逆正接を導出する方法を学びます。さらに、このタイプの導関数の例を確認したり、逆正接の導関数に関する演習を解いて練習したりすることもできます。最後に、逆正接の導関数の公式の証明も示します。

逆正接の導関数は何ですか?

x の逆正接の導関数は、1 の 1 に x の 2 乗を加えたものです。

$f(x)=\text{arctan}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1+x^2}$

したがって、関数の逆正接の微分値は、その関数の微分値を 1 で割った商に、その関数の 2 乗を加えたものに等しくなります。

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

この場合、関数は au で表されるため、これは関数 u の逆正接の導関数の式になります。

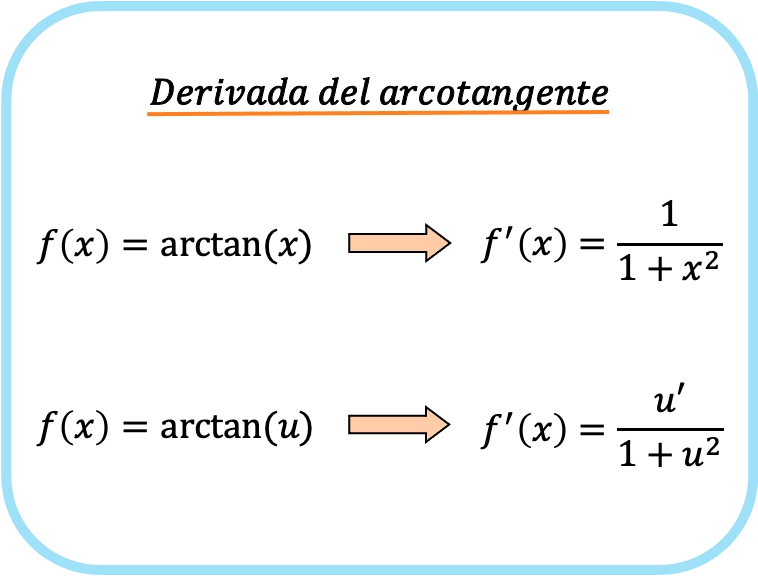
ご覧のとおり、逆正接の導関数の公式は、逆正弦および逆余弦の導関数の公式と非常によく似ています。

逆正接の導関数の例

逆正接の導関数の公式がわかったら、このタイプの三角関数導関数のいくつかの例の導出について説明します。こうすることで、関数の逆正接がどのように導出されるのかを理解しやすくなります。

例 1: 2x の逆正接の導関数

$f(x)=\text{arctan}(2x)$

次の式を適用して導関数を解きます。

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

2x の微分値は 2 なので、2x の逆正接微分値は 2 に 1 を加えたものに 2x の 2 乗を加えたものになります。

$f(x)=\text{arctan}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{1+(2x)^2}}=\cfrac{2}{1+ 4x^2}$

例 2: x の 2 乗の逆正接の導関数

$f(x)=\text{arctan}(x^2)$

この例の導関数の結果を求めるには、逆正接の導関数の公式を使用する必要があります。これは次のとおりです。

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

したがって、関数 x ²の導関数は 2x であるため、x の逆正接の 2 乗の導関数は次のようになります。

$f(x)=\text{arctan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{1+\left(x^2\right)^2}=\cfrac{2x}{1+x^4}$

例 3: x のサインの逆正接の導関数

$f(x)=\text{arctan}\bigl(\text{sen}(x)\bigr)$

論理的には、導関数を計算するには、対応する式を適用する必要があります。

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

この場合、合成関数があるため、逆正接の導関数を計算するには連鎖規則を適用する必要があります。

$f(x)=\text{arctan}\bigl(\text{sen}(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{\text{cos}(x)}{1+\text{sen}^2(x)}$

逆正接の微分に関する演習を解決しました

次の逆正接関数を導出します。

$\text{A) } f(x)=\text{arctan}(x^3)$

$\text{B) } f(x)=\cfrac{\text{arctan}(3x^4)}{2}$

$\text{C) } f(x)=\text{arctan}(x^5-3x^3+10)$

$\text{D) }f(x)=\text{arctan}^3(4x^2)$

$\text{E) }f(x)=\text{arctan}\bigl(\ln(x)\bigr)$

$\text{F) } f(x)=\text{arctan}\left(\sqrt{x^2+2x}\right)$

解決策を見る

$\text{A) } f'(x)=\cfrac{3x^2}{1+\left(x^3\right)^2}=\cfrac{3x^2}{1+x^6}$

$\text{B) } f'(x)=\cfrac{12x^3}{2\left(1+\left(3x^4\right)^2\right)}=\cfrac{6x^3}{1+9x^8}$

$\text{C) } f'(x)=\cfrac{5x^4-9x^2}{1+\left(x^5-3x^3+10\right)^2}$

$\text{D) } f'(x)=3\text{arctan}^2(4x^2)\cdot \cfrac{8x}{1+\left(4x^2\right)^2}=\cfrac{24x\cdot\text{arctan}^2(4x^2)}{1+16x^2}$

$\text{E) } f'(x)=\cfrac{\cfrac{1}{x}}{1+\bigl(\ln(x)\bigr)^2}=\cfrac{1}{x\left(1+\ln^2(x)\right)}$

$\text{F) } f'(x)=\cfrac{1}{1+\left(\sqrt{x^2+2x}\right)^2}\cdot \cfrac{2x+2}{2\sqrt{x^2+2x}}=\cfrac{x+1}{\left(1+x^2+2x\right)\sqrt{x^2+2x}}$

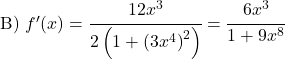
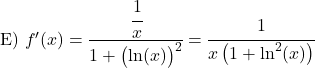
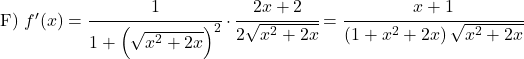
逆正接の導関数の公式のデモンストレーション

次に、逆正接の導関数の公式を証明します。

$y=\text{arctan}(x)$

まず、逆正接が正接の逆関数であるという事実を利用して、逆正接を正接に変換します。

$x=\text{tan}(y)$

方程式の両辺を微分します。

$1=\cfrac{1}{\text{cos}^2(y)}\cdot y'$

消去して、’:

$y'=\text{cos}^2(y)$

一方、基本的な三角関数の恒等式のおかげで、サインとコサインの二乗の和は 1 に等しいことがわかります。したがって、前の式を分数に変換できます。

$\text{sen}^2(y)+\text{cos}^2(y)=1$

$y'=\cfrac{\text{cos}^2(y)}{1}=\cfrac{\text{cos}^2(y)}{\text{sen}^2(y)+\text{cos}^2(y)}$

すべての項をコサインの二乗で割ります。

$y'=\cfrac{\cfrac{\text{cos}^2(y)}{\text{cos}^2(y)}}{\cfrac{\text{sen}^2(y)}{\text{cos}^2(y)}+\cfrac{\text{cos}^2(y)}{\text{cos}^2(y)}}$

$y'=\cfrac{1}{\cfrac{\text{sen}^2(y)}{\text{cos}^2(y)}+1}$

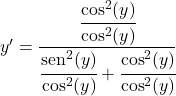
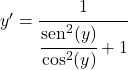
サインをコサインで割った値はタンジェントに等しいため、次のようになります。

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

$y'=\cfrac{1}{\text{tan}^2(y)+1}$

上で見たように、タンジェントは変数 x と同等なので、式を代入して逆正接の導関数の式を得ることができます。

$y'=\cfrac{1}{x^2+1}$

逆正接の導関数は何ですか?

逆正接の導関数の例

例 1: 2x の逆正接の導関数

例 2: x の 2 乗の逆正接の導関数

例 3: x のサインの逆正接の導関数

逆正接の微分に関する演習を解決しました

逆正接の導関数の公式のデモンストレーション

コメントする 返信をキャンセル

コメントする返信をキャンセル