このページでは、ルフィニの法則を適用して多項式を分割する方法を説明します。解説に加えて、ルフィニ則を使った多項式の割り算を段階的に解く例題や演習も見ることができます。さらに、この方法の応用例がすべて見つかり、実際、複数の応用例がきっとあなたを驚かせるでしょう。
ルッフィーニの法則とは何ですか?
数学におけるルフィニの法則は、任意の多項式をxr形式の多項式ですばやく除算できる代数的手法です。ルッフィーニの法則は、この方法を発明した数学者パオロ ルッフィーニにちなんで名付けられました。
ただし、ルフィニの法則は多項式の除算に使用されるだけでなく、他にも多くの用途があります。たとえば、ルフィニの法則は、多項式の根を求めたり、多項式の数値を求めたり、多項式を因数分解したり、3 次以上の方程式を解くためにも使用されます。以下では、これらすべての操作を実行できるようにルフィニのルールがどのように適用されるかを見ていきます。
最後に、ルフィニの法則は、ルフィニの方法、ルフィニの定理、または多項式の合成除算としても知られています。
ルッフィーニの法則の適用方法
これまで見てきたように、ルフィニの規則の主な用途は、多項式を二項式で除算すること、つまり次のタイプの除算を行うことです。
![]()
ルッフィーニの規則を使用するには、除算多項式が常にx (係数が 1 に等しい)と数値(正または負) で形成されている必要があることに注意してください。そうでない場合は、ルッフィーニ アルゴリズムを使用できません。
ルッフィーニのルールを適用するには、手順全体に従う必要があるため、以下では例を段階的に解決して、ルッフィーニのルール (またはルッフィーニの方法) がどのように適用されるかを確認します。
ルッフィーニの法則の例
- ルフィニの法則を使用して、次の多項式の除算を解きます。
![]()
まず、互いに交差する 2 本の垂直線を描き、次に被除数と除数を次のように配置する必要があります。
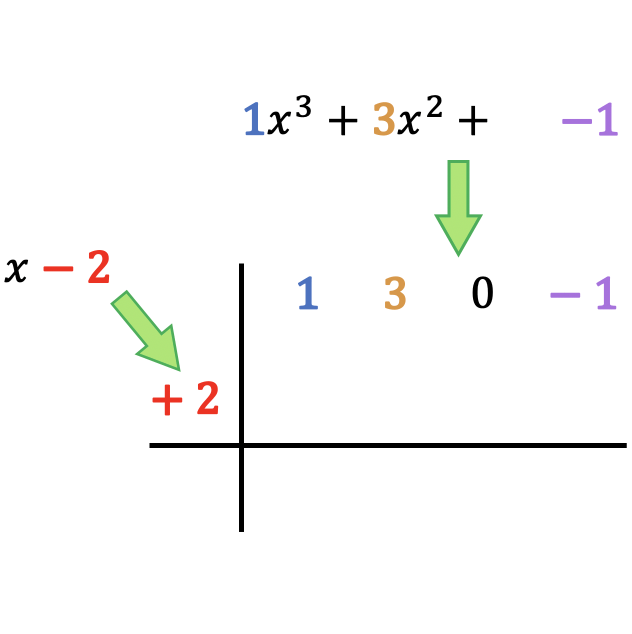
ご覧のとおり、被除数多項式の係数を最高次数から最低次数の順序で一番上に配置し、除数多項式の独立項を符号を変えてボックスの左側に配置する必要があります。
警告:被除多項式に特定の次数の項がない場合 (不完全多項式)、その場所に 0 が置かれます。たとえば、この場合、多項式は
![]()
次数 1 の単項式がないので、その場所に 0 を置きます。
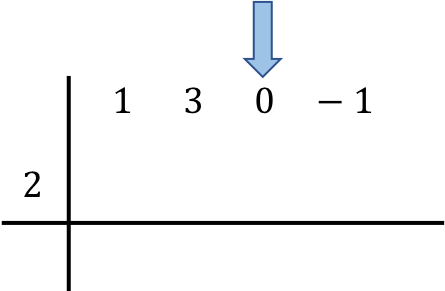
演算に関係する多項式を配置したら、最初の数値を下の行に直接降下します。
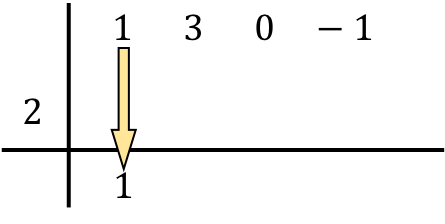
ここで、ルフィニのルールを特徴づけるステップが始まります。下の数値と左側の数値を掛けて、その結果を次の列に入れます。
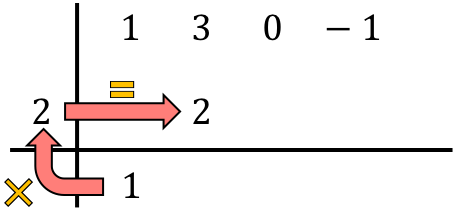
そして列の数値を加算し、合計の結果をすぐ下に置きます。
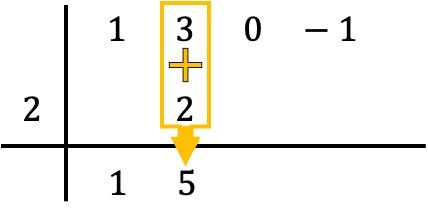
つまり、ルフィニの方法では、このプロセスを繰り返す必要があります。そこで、同じことをもう一度行います。下の数値と左側の数値を掛け、その結果を次の列に入れ、最後に縦に並んだ数値を加算します。
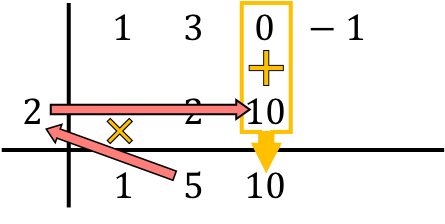
そして最後まで同じ手順を続けて繰り返します。まず下の数値と左側の数値の積を計算し、次に結果を次の列に配置し、最後に同じ列の数値を加算します。
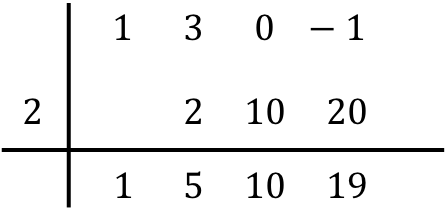
したがって、すべての列を埋めると、多項式の除算が完了したことになります。
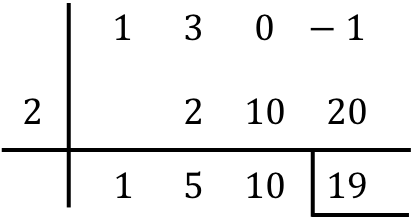
したがって、多項式を除算した結果を見つける必要があるだけです。
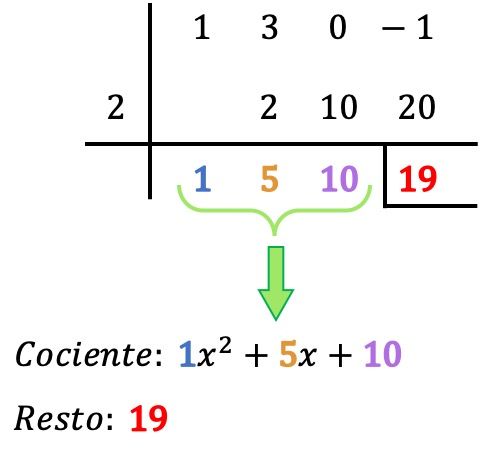
- 2 つの多項式間の除算の余りは、下の行の最後の数値です。したがって、この場合、余りは 19 に等しくなります。剰余は、通常、左側にバーを配置し、その数値の下に別のバーを配置することによって示されます。
- 多項式除算の商は、多項式商の係数である、取得された他の値によって決定されます。右から最初の桁は 0 年生の学期の係数、次の桁は 1 年生の学期の係数、その次は 2 年生、その次は 3 年生…というように最後まで続きます。 。それで:
ルッフィーニの法則の解決された演習
以下に、ルフィニの法則に関する段階的な演習をいくつか示します。これにより、この方法で多項式の除算を解く方法を練習して理解することができます。各演習を試してから、修正を見て正しく実行できたかどうかを確認することをお勧めします。
演習 1
ルッフィーニの法則を使用して、次の多項式の除算を実行します。
![]()
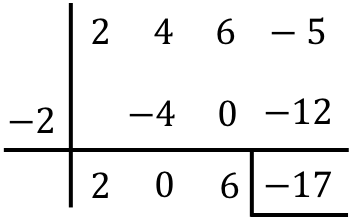
したがって、2 つの多項式間の除算の結果は次のようになります。
商:
![]()
休む:
![]()
演習 2
ルフィニの法則を使用して、次の多項式の除算を計算します。
![]()
この特定のケースでは、被除数多項式には 2 次の項がないため、その場所にゼロを置く必要があります。
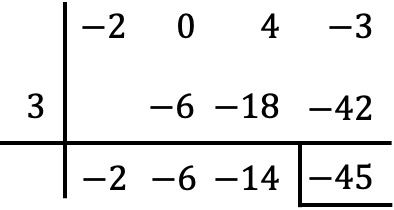
したがって、2 つの多項式間の除算の結果は次のようになります。
商:
![]()
休む:
![]()
演習 3
ルフィニの法則による次の多項式の除算の結果を求めます。
![]()
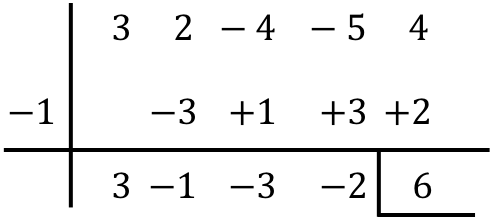
結論として、2 つの多項式を除算した結果は次のようになります。
商:
![]()
休む:
![]()
演習 4
次の多項式の除算の余りが 5 に等しくなるような未知のmの値を求めます。
![]()
除数は(xr)または(x+r) の形式であるため、ルフィニの法則を適用して除算を解くことができます。したがって、未知の m をドラッグすることで Ruffini の方法を適用します。
ここで、剰余は 5 でなければならないため、得られた剰余を 5 に等しくします。
![]()
そして方程式を解いてパラメーターmの値を見つけます。
![]()
![]()
したがって、変数mが 3 に等しい場合、多項式間の除算の余りは 5 に等しくなります。
演習 5
次の多項式の除算の余りが 3 になるように、パラメーターmの値を決定します。
![]()
除数は(xr)または(x+r) の形式であるため、ルフィニの法則を適用して除算を解くことができます。したがって、未知の m をドラッグすることで Ruffini の方法を使用します。
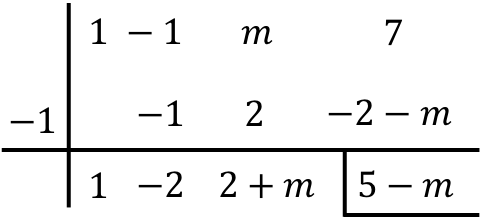
最後の乗算では、分配特性に留意してください。
![]()
一方、除算の余りの計算は次のようになります。
![]()
![]()
![]()
除算の余りは 3 に等しくなければならないため、結果の剰余式を 3 に等しくします。
![]()
そして、結果として得られた方程式を解いて、パラメーターmの値を決定します。
![]()
![]()
![]()
![]()
したがって、多項式の除算の余りが 3 になるには、 mが 2 に等しくなければなりません。
ルッフィーニの法則のさらなる応用
説明したように、ルフィニの法則は主に多項式間の除算を実行するために使用されます。ただし、ルフィニの規則は他の計算の実行にも使用されます。以下でそれぞれについて説明します。
多項式の根
多項式の根は、ルフィニの法則を使用して簡単に決定できます。多項式の根がわからない場合は、その定義を確認してみましょう。
多項式の根 (またはゼロ) は、多項式をキャンセルする値です。言い換えれば、多項式の根は、多項式で評価されたときに 0 に等しい数値を持つすべての値です。
![]()
一方、剰余定理のおかげで、与えられた値に対する多項式の数値が
![]()
はゼロであり、必然的に次の多項式を除算した余りになります。
![]()
これも 0 である必要があります。
![]()
したがって、ルフィニの法則を使用して多項式を除算すると、
![]()
別の形式の多項式の間
![]()
0 に等しい剰余が得られます。これは、次のことを意味します。
![]()
多項式の根です
![]()
例を挙げると、次のことがよりよく理解できるでしょう。
- どうかを確認してください
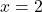
多項式の根です
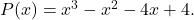
指定された値が多項式の根であるかどうかを確認するには、単にその多項式とその値を使用して Ruffini 法を適用します。
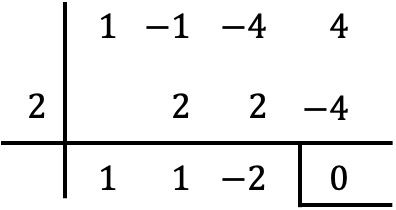
ルッフィーニの法則によって得られた剰余はゼロに等しいため、これは実質的に次のことを意味します。
![]()
多項式の根です
![]()
多項式の因数分解
ルッフィーニの法則は、階乗多項式に通常適用される方法です。これにより、3次、4次、5次などの多項式の根をすべてすばやく知ることができるためです。
それでは、例を使用してルフィニのアルゴリズムで多項式を因数分解する方法を見てみましょう。
- 次の 3 次多項式を因数分解します。
![]()
最初に行うことは、多項式の根をすべて見つけることです。そして、多項式の考えられる根は独立項の約数であり、この場合は 6 です。
多項式の可能な根: +1、-1、+2、-2、+3、-3、+6、-6
ここで、ルフィニの法則を使用して、これらの各値間の多項式を除算してみる必要があります。除算の余りが 0 の場合、その値が多項式の根であることを意味します。ただし、除算の余りが 0 以外の場合、その値は多項式の根ではありません。したがって、すべての数値を使用してルフィニのルールをテストすると、次の 3 つのケースでのみ残りがキャンセルされます。
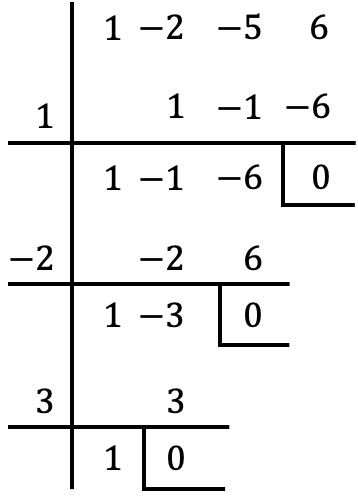
したがって、問題における多項式の根は、剰余が消える値、つまり次のとおりです。
![]()
最後に、多項式を因数分解するには、各根を表現する必要があります
![]()
型の因子の形式で
![]()
つまり、ルートごとに括弧を付ける必要があります。
![]()
そして見つかったルートの符号が変わりました。
![]()
ご覧のとおり、ルフィニの法則を使用して多項式を因数分解することができました。ただし、多項式の因数分解は非常に複雑なトピックであるため、疑問を抱いたことがあるかもしれません。この場合、私たちの Web サイト (右上の検索エンジン) で、多項式の因数分解方法に関する記事を検索できます。そこで詳しく説明しており、段階的に解決する演習を行うことができます。さらに、多項式を因数分解する他の方法も示します。
多項式の数値を計算する
意外に思われるかもしれませんが、多項式の数値は剰余定理を使用したルフィニの法則によって決定できます。
しかし、明らかに、これを行うには剰余定理を知る必要があります。そうでない場合は、当社の Web サイト (右上の検索エンジン) で剰余定理の説明を検索してください。
したがって、剰余定理のおかげで、任意の多項式の数値を知ることができます。例を使用してこれを行う方法を見てみましょう。
- の数値を計算します。

のために
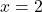
ルフィニの法則を適用すると、
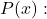
![]()
値の多項式の数値を求めるには
![]()
私たちがしなければならない唯一のことは、多項式とその値でルフィニの規則を使用することです。
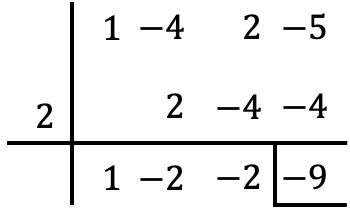
したがって、剰余定理から、多項式の数値は多項式の除算の剰余と一致することがわかります。したがって、次の多項式の数値は
![]()
-9です。
![]()
一方、数値を計算することで、ルフィニのルールが正しく適用されていることを確認できます。
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c935b3276a3915dbdf93755851ef28e5_l3.png)
3次以上の方程式を解く
ルッフィーニの法則のもう 1 つの応用は、2 を超える次数の方程式を解くことです。これらの場合、2 次方程式のような公式は存在しないからです。例を使用してこれを行う方法を見てみましょう。
- ルフィニの法則を使用して次の二次方程式を解きます。
![]()
方程式を多項式であるかのように扱う必要があります。次に、 2 次方程式が得られるまで、ルフィニの法則を使用して「多項式」の根をできるだけ多く計算する必要があります。この場合、それは次数 3 の方程式であるため、「多項式」の根を決定するだけで十分です。
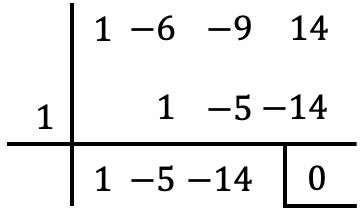
したがって、方程式の解は次のようになります。
![]()
他の解を見つけるには、ルフィニの法則の商で得られた多項式を 0 に等しくする必要があります。
![]()
そして、結果の二次方程式を対応する式で解きます。
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a57aa9f04a1053566c6a53b65afa008a_l3.png)
結論として、3 次方程式の 3 つの解は次のとおりです。
![]()