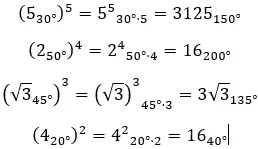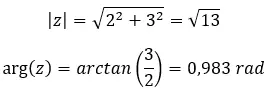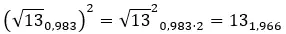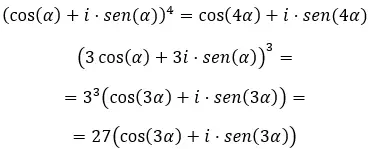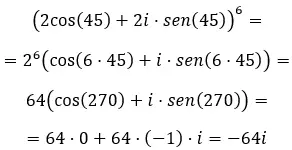正しい方法を知っていれば、複素数の累乗を解くことは非常に簡単です。したがって、この記事では、二項形式、極形式、三角形式の複素数の 3 つの方法で複素累乗を解く方法を説明します。
複素数の累乗を解くにはどうすればよいですか?
冒頭で述べたように、複雑な権限を使用して動作する場合、3 つの状況が発生する可能性があります。最初の最も単純な方法は、数値が極形式で与えられる場合です。 2 番目は二項形式で数値が与えられた場合、三番目は三角形式で数値が与えられた場合です。
言い換えれば、極形式の複合体を操作すると、演習をより迅速に解くことができます。したがって、問題の数値を極形式に変換することをお勧めします。しかし実際には、どの方法も簡単に解決できます。そうは言っても、すべてのケースがどのように解決されるかを説明し、演習を提供します。
極形式の複素数のべき乗
複素累乗を極形式で解きたいときは、単純に係数を any に上げ、引数に n を乗算します。数学的に表現すると、次の式が得られます。
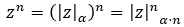
以下にいくつかの例を示しますので、自分で解決してみてください。
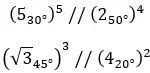
二項形式の複素数のべき乗
一方、二項形式で複素累乗を解きたい場合は、2 つの異なる方法を使用できます。 1 つ目は、「代数的」方法でべき乗を解くことを扱います (i が変数であるかのように解決します)。 2 番目のシステムは、二項形式を極形式に変換してから、前の手順に従うものです。
二項形式から極形式に移行する方法がわからない場合は、複素数に関する記事でわかりやすく説明しています。ただし、ここでは例を使って簡単に説明します。
次の複素累乗を解いてみてください: (2 + 3i) 2 。
三角関数形式の複素数のべき乗
最後に、三角関数形式で複素累乗を解きたいときは、よく知られたド モアブルの公式を使用する必要があります。それは次のように書かれています。
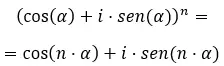
この公式を理解した上で、次の演習を解いてみてください。