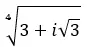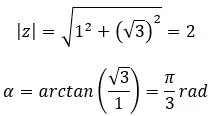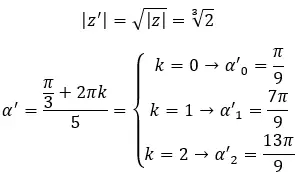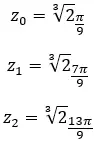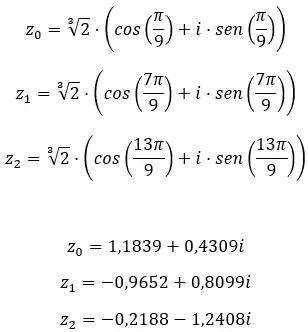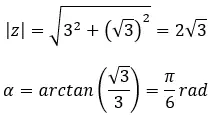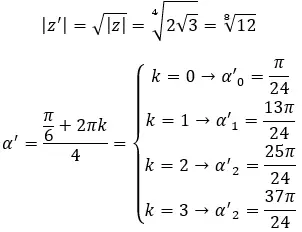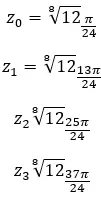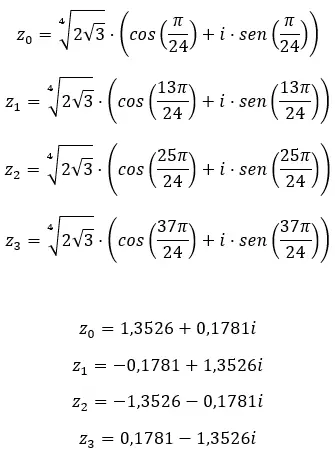複素数の根を計算するのは非常に簡単です。まあ、手順を理解すると、かなりの繰り返しになります。次に、それを説明し、例を挙げて実際の演習での応用方法を学びます。
複素数の n 乗根
n 乗根の概念は n 次の乗根と同じなので、複素数の平方根と 5 乗根を計算するのに同じ方法が使用されます。もちろん、この順序によって解の数は変わります。
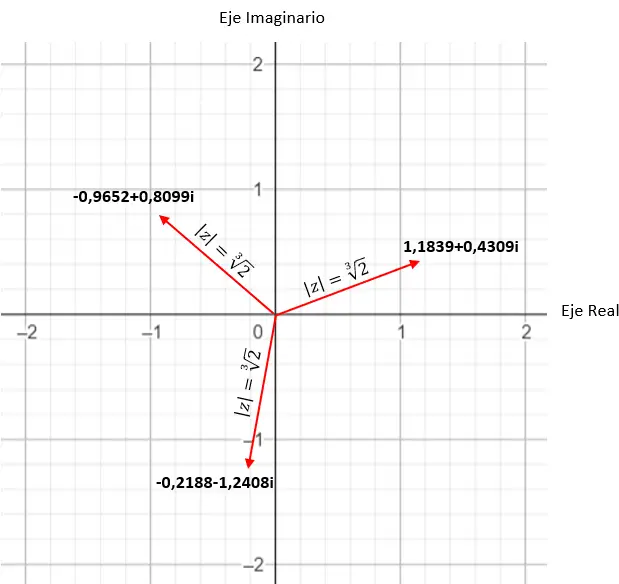
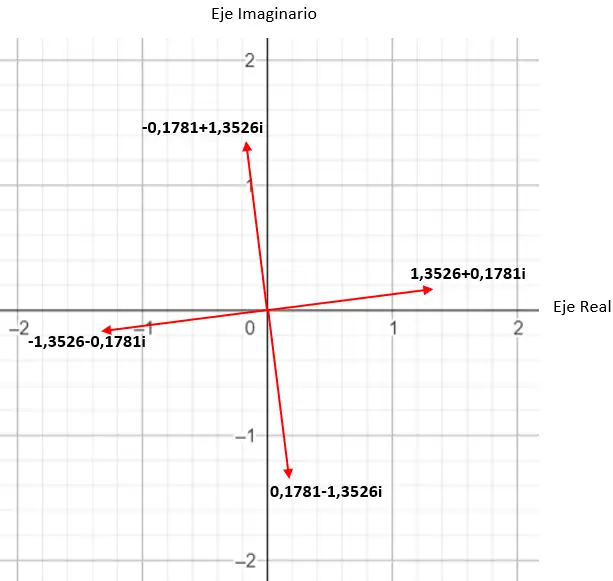
たとえば、複素数の 4 番目の根を計算すると、4 つの異なる解が得られます。そしてそれを複素平面で表現すると、平面の原点を中心とした4辺の正多角形が形成されることがわかります。これは非常に興味深いプロパティであり、後で (例のセクションで) 詳細に説明します。
この概念を明確にしたので、極形式で複素数の根を計算する方法を見ていきます (根を解くには、この表記を使用するのが最も簡単です)。単純に、係数の根を計算し、引数を n で表現する必要があります。つまり、次の複素数 (z) の根です。
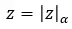
これらの計算対象となる金額は次のとおりです。
- モジュール:初期モジュールの n 番目のルート。
- 引数:引数にラジアンで 2πk または度で 360k を加え、n で割ります。
数学的には、モジュールと引数を計算するには、次の 2 つの式を使用します。
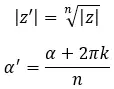
ここで、k = 0、1、2、…、n-1。
したがって、結果を次のように表現します。
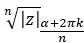
明確にするために、このルートを解くことで得られる n 個の解は、同じモジュールと n 個の異なる引数によって形成されます。
複素数の n 乗根の計算例
次に、複素数の n 乗根を計算する例をいくつか見ていきます。ご自身で問題の解決を試み、完了したら修正内容を確認することをお勧めします。方法は上で説明していることを忘れないでください。
複素数の 3 番目の根を求めます: 1 + i √3 。
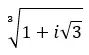
複素数の 4 番目の根を求めます: 3+i √ 3 。