このページでは、ゼロポテント行列とは何かについての説明と、それを理解して疑問を持たないようにいくつかの例を示します。さらに、零ポテント行列の構造と、これらのタイプの行列のすべてのプロパティを確認できるようになります。
ゼロポテント行列とは何ですか?
ゼロポテント行列の定義は次のとおりです。
零ポテント行列は、整数に累乗するとゼロ行列となる正方行列です。
![]()
金
![]()
はゼロポテント行列であり、
![]()
ゼロ行列を与えるべき乗の指数。
この条件は、零能行列の累乗が指数に関係なく常にゼロになることを意味するのではなく、むしろ、結果が 0 でいっぱいの行列になる行列の累乗が少なくとも 1 つ存在する場合、その行列は零能であることを意味します。
一方、虚数行列の虚数指数は、虚数条件を満たす最小の数です。また、 nilpotent 行列は次数kであるとも言えます。ここで、 kはその nilpotency インデックスです。
零ポテント行列の例
零ポテント行列の概念を理解するために、このタイプの行列の例をいくつか見ていきます。
2 × 2 の虚数行列の例
次の次元 2×2 の正方行列はゼロポテントです。
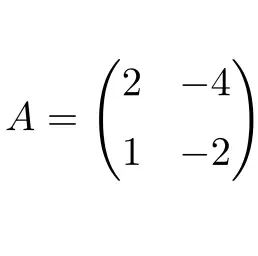
行列 A を二乗すると結果としてゼロ行列が得られるため、行列は零能です。
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fde370dd31b0e2a533fdf1e9d23cf2c9_l3.png)
したがって、ゼロ行列は 2 乗で得られるため、これは零行列であり、零行列の指数は 2 です。
3×3 虚数行列の例
次の次数 3 の正方行列はゼロポテントです。
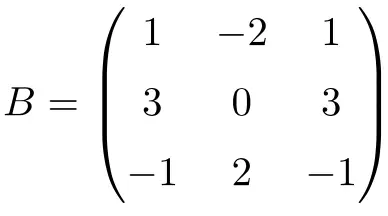
ただし、行列を 2 に引き上げても、ゼロ行列は得られません。
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fbad4ccc270e2960ae50cc23eacc7530_l3.png)
しかし、行列の 3 乗を計算すると、すべての要素が 0 に等しい行列が得られます。
![Rendered by QuickLaTeX.com \displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-da876a04b14d80c156e24c95bd22372e_l3.png)
したがって、行列 B は虚数行列であり、ゼロ行列は 3 乗で得られるため、その虚数インデックスは 3 になります。
2 × 2 虚数行列の構造
以下に、すべての nilpotent 行列の構造を示します。その証明は少し面倒なので、次数 2 のゼロポテント行列を取得する公式を直接残しておきます。
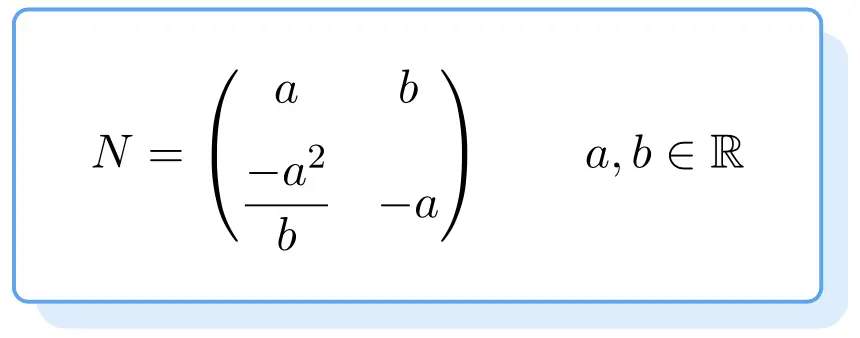
したがって、上記の式を満たす行列はすべてゼロポテント行列になります。このための値は、
![]()
そして
![]()
実数であれば任意に指定できます。
零ポテント行列の性質
零ポテント行列には次の特徴があります。
- 零ポテント行列のトレースは常にゼロです。
- 同様に、任意の零能行列の行列式は常に 0 です。ただし、その逆は当てはまりません。つまり、行列の行列式が 0 であることは、行列が零点であることを意味しません。
- 対角化できる唯一の零行列はゼロ行列です。
- 次元n × nの虚数行列の虚数インデックスは、常にn以下です。これが、2 × 2 虚数行列の虚数インデックスが常に 2 になる理由です。
- 零ポテント行列は可逆ではありません。
- 主対角線上にゼロがある三角行列も、零ポテント行列です。
- 行列が次の場合、という定理があります。

がゼロの場合、行列は
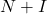
は可逆です。ここで、
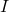
は単位行列です。さらに、その逆行列は次の式で求められます。
![]()
- 同様に、もし

が零ポテント行列の場合、行列の逆行列を計算できます。
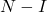
次の方程式を使用します。
![]()
- 任意の特異行列、つまり非可逆行列は、ゼロポテント行列の積に分解できます。
- 零ポテント行列のすべての固有値 (または固有値) はゼロです。
![]()
- 最後に、興味深いことに、線形アプリケーションを定義する nilpotent 変換の概念もあります。
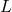
次のようなベクトル空間の
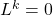
。