虚数の集合または虚数単位について聞いたことがあるでしょう。これは、実数に属さない数値を表現する数学的必要性から生まれた数学的概念です。
虚数とは何ですか?
虚数とは、二乗すると負の数になる数です。したがって、これらは負の数の平方根に相当する値です。たとえば、虚数単位 (数値 i) は -1 の平方根に等しくなります。
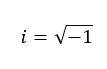
実数セットでは負の根を解決できないため、これらの数値は実数には属しません。ここに想像上の設定の重要性があります。このセットは、負の根を処理できるように、また負の根を与えるため「解がない」方程式や二次問題をすべて解けるように発明されました。
混乱を避けるために、虚数と複素数を区別することが重要です。複素数は、実数と虚数から構成される数です。したがって、虚数は実体部分を持たない複合体のサブカテゴリーです。次の表を見ると、違いがよくわかります。
| 複素数 | ロイヤルパーティー | 想像の部分 | 説明 |
| 4+7i | 4 | 7i | 複雑な |
| 3 | 3 | 0 | 純粋なロイヤル |
| 2i | 0 | 2i | 純粋な想像力 |
このデジタル セットの配置を完了するには、次の画像ですべてのセットの構造を視覚化できます。ご覧のとおり、複素数にはあらゆる種類の数値が含まれており、これらは実数と純粋虚数 (この記事で扱う虚数) に分類できます。

虚数の例
虚数単位 (i) から、他の虚数を推定できます。次の式を適用するだけです。
メートル=リ
ここで、m は虚数、r は実数、i は虚数単位です。次の画像では、負のルートからさまざまな虚数を取得する方法がわかります。
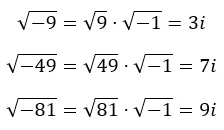
実際、これを次の式に推定できます。
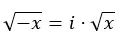
虚数の性質
虚数には非常に興味深い特性が多数あります。この記事の冒頭ですでに説明したものもあれば、そうでないものもあります。
- 虚数は物理的に存在せず、私たちの現実では表現できない数値であるため、一連の現実には属しません。
- これらは負のルートに相当する値です。
- それらは想像上の直線上にグラフィカルに表すことができます。
- 虚数乗 (これは次のセクションで説明する概念です) は、虚数を含む数値計算を簡素化するのに非常に役立ちます。
- オイラーの公式は、虚数を実数に関連付けることができる式です。
虚数を使った演算
虚数の重要な特性をすべて理解したので、次は虚数を使用して演算を解く方法を学習します。虚数を操作するには、虚数乗という 1 つの概念を考慮する必要があることを除いて、実数を操作する場合と同じ手順に従う必要があります。
想像力
虚数には、虚数単位を単独で乗算すると発生する非常に興味深い特性があります。つまり、虚数統一の累乗を行うと、これが起こります。次のリストのようにパワーを書き留めると、パターンが見つかります。
i 0 = 1
I 1 = 私
i 2 = i · i = ( √ -1) · ( √ -1) = -1
i 3 = i 2 i = (-1) i = -i
i 4 = i 2 i 2 = (-1) (-1) = 1
この概念を理解すると、難しい演算を簡略化して少し簡単にすることができるため、虚数を使った演算を解くことがはるかに簡単になります。また、これらのパワーの良い点は、それらが無期限に繰り返されることです。さらにいくつかの権限を追加すると、これがわかります。
私5 = 私
i 6 = -1
i 7 = -i
i 8 = 1
等
そして、負の力でもこれは起こります。
虚数を使った算術演算
次に、それぞれの基本的な四則演算の例を示して、虚数の計算を解いていきます。
- 虚数の追加:実数の追加とまったく同じですが、i を追加することを忘れないでください。
4i + 3i = 7i
- 虚数の減算:減算も実数セットと同じ方法で解決されます。
4i – 3i = I
- 虚数の乗算:この場合、前に述べた虚数乗を念頭に置く必要があります。
3i 4i = 12 i 2 = 12 (-1) = -12
- 虚数の除算:このタイプの除算では、虚数乗に遭遇した場合に備えて警戒する必要があり、これにより演算を簡素化できます。
12i ÷ 4i = 3
虚数を使った方程式
前に述べたように、実際の集合で方程式を解くと、負の根が得られることがあるため、方程式には「解がありません」 。しかし、虚数がわかったので、これらの方程式を解くことができます。例を見てみましょう:
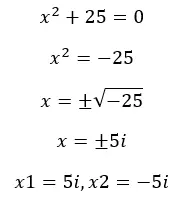
虚数は何に使われますか?
虚数は、実際の集合の外にある値を表現できる必要性から生じます。そのため、最初は便利なアプリケーションがあまりないように見えるかもしれません。しかし、真実はまったく逆です。それらを実数と組み合わせると複素数が得られるからです。
そして、これらには多くの用途があります。それらは交流を研究するために使用され(交流には負の値があるため)、その使用は波動の分野でも非常に広く使用されています(物理学、電気通信エレクトロニクス、量子力学に応用されています)。他にも多くの用途があります。
さらに、二次方程式を解くときに、その値がマイナスの根となって演算ができないことがよくあります…虚数を使えば解けます。結論としては、より抽象的な知識を拡張できるセットであると言えます。