空間内の点から平面までの距離 (公式)

このページでは、空間内の点と平面の間の距離を計算する方法 (公式) を説明します。さらに、例を見て、段階的に解決される演習で練習することができます。

点から平面までの距離はどれくらいですか?

解析幾何学では、点から平面までの距離は、その点と平面上の他の点との間の最短距離です。この距離は、点から平面に向かう、平面に垂直な線分の長さに対応します。

点から平面までの距離の公式

点と平面の間の距離の概念を正確に理解したら、次はその距離を計算する式を見てみましょう。

点と平面の一般 (または暗黙の) 方程式が与えられると、次のようになります。

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

点から平面までの距離の公式は次のとおりです。

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

点から面までの距離の公式の証明は非常に面倒で長いため、このページでは行いません。

一方、式を適用したときにゼロに等しい結果が得られた場合、これは明らかに、点と平面の間の距離がゼロであり、したがって点はその平面の一部であることを意味します。

最後に、式を適用するには、計画を一般 (または暗黙的な) 方程式として定義する必要があることに注意してください。したがって、別の種類の平面方程式で表す場合は、まず一般方程式に変換してからその式を使用する必要があります。

点から平面までの距離の計算例

点と平面の間の距離が数値的にどのように決定されるかを理解できるように、以下の例を解いてみます。

点 P と平面 π の間の距離を計算します。要点と計画を述べた上で、次のようにします。

$P(1,3,-2) \qquad \qquad \pi: \ 2x+5y-4z+7=0$

点から平面までの距離を求めるには、上のセクションで示した式を適用するだけです。

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

ここで、それぞれの未知の値を式に代入します。

$d(P,\pi) = \cfrac{\lvert 2\cdot 1+5\cdot 3-4\cdot (-2)+7\rvert}{\sqrt{2^2+5^2+(-4)^2}}$

そして最後に、次の操作を実行します。

$d(P,\pi) = \cfrac{\lvert 2+15+8+7\rvert}{\sqrt{4+25+16}}$

$\bm{d(P,\pi) = }\cfrac{\bm{32}}{\bm{\sqrt{45}}}$

分数の分子には絶対値があり、分母には平方根があるため、結果は常に正でなければならないことに注意してください。距離は負にはならず、常に正であるため、これは理にかなっています。

2 つの平行な平面間の距離を計算します

2 つの平行な平面は常に同じ距離離れているため、2 つの平行な平面間の距離を見つけるには、2 つの平面の一方の点を取得し、その点からもう一方の平面までの距離を計算できます。

2つの平行な面の間の距離を求める方法です。ただし、2 つの平面の方程式の係数 A、B、C が一致する場合、これを行うさらに簡単な方法があります。

2 つの平行な平面の一般 (または暗黙的な) 方程式を考えてみましょう。

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

2 つの平行な平面間の距離を計算する式は次のとおりです。

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

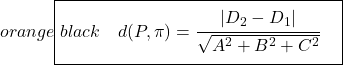
したがって、公式を使用して 2 つの平行な平面の間の距離を見つけるのは確かに簡単です。公式を適用するだけで済むためですが、それは問題によって異なります。さらに、距離を計算する両方の方法について説明し、好みの方法を選択できるようにすることが最善であると考えます。

2 つの平行な平面間の距離の計算例

例として、次の 2 つの平面間の距離を計算します。

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

まず、2 つの平行な平面を扱っていることを確認する必要があります。したがって、平面方程式のすべての係数は独立項を除いて比例するため、事実上 2 つの平行な平面になります。

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

この場合、2 つの平面の方程式の項 A、B、C は一致しませんが、2 番目の平面の方程式全体を 2 で割ることによってこれを実現できます。

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

したがって、2 つの平面の方程式にはすでに同じ係数 A、B、C が含まれています。したがって、2 つの平行な平面間の距離の公式を使用して、2 つの平面間の距離を簡単に計算できます。

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

値を代入して演算を解決します。

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

つまり、一方の平面ともう一方の平面の間の距離は 1 に等しくなります。

点から平面までの距離の問題を解く

演習 1

点 P と、デカルト (または一般) 方程式が次のような平面との間の距離を計算します。

$P(2,0,-1) \qquad \qquad \pi: \ x-3y+2z-4=0$

解決策を参照

点から平面までの距離を計算するには、対応する式を使用する必要があります。

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

各パラメータの値を式に代入します。

$d(P,\pi) = \cfrac{\lvert 1\cdot 2+(-3)\cdot 0+2\cdot (-1)-4\rvert}{\sqrt{1^2+(-3)^2+2^2}}$

そして最後に、次の操作を実行します。

$d(P,\pi) = \cfrac{\lvert 2+0-2-4\rvert}{\sqrt{1+9+4}}$

$d(P,\pi) = \cfrac{\lvert -4\rvert}{\sqrt{14}}$

$\bm{d(P,\pi) = }\cfrac{\bm{4}}{\bm{\sqrt{14}}}$

演習 2

点 P と平面 π の間の距離を求める：

$P(-1,4,3) \qquad \qquad \pi: \ y=5x-2z$

解決策を参照

点から平面までの距離の公式を使用する前に、まず平面を陰的な (または一般的な) 方程式の形式で表現する必要があります。

$\pi: \ -5x+y+2z=0$

これで、式を使用して点から平面までの距離を決定できるようになりました。

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

各項の値を式に代入します。

$d(P,\pi) = \cfrac{\lvert -5\cdot (-1)+1\cdot 4+2\cdot 3+0\rvert}{\sqrt{(-5)^2+1^2+2^2}}$

そして最後に、次の操作を実行します。

$d(P,\pi) = \cfrac{\lvert 5+4+6\rvert}{\sqrt{25+1+4}}$

$\bm{d(P,\pi) = }\cfrac{\bm{15}}{\bm{\sqrt{30}}}$

演習 3

点と平面の間の距離の公式を使用して、点 P が平面 π 内にあるかどうかを判断します。

$P(0,-3,5) \qquad \qquad \pi: \ 4x+6y+2z+8=0$

解決策を参照

点が平面に属しているかどうかを確認するには、2 つの間の距離を計算します。距離が 0 の場合、これは点が平面に属していることを意味します。一方、距離が 0 以外の場合、これは、点が平面に属していることを意味します。点は平面の外側にあります。プラン。

したがって、次の式から点と平面の間の距離を決定します。

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

$d(P,\pi) = \cfrac{\lvert 4\cdot 0+6\cdot (-3)+2\cdot 5+8\rvert}{\sqrt{4^2+6^2+2^2}}$

$d(P,\pi) = \cfrac{\lvert -18+10+8\rvert}{\sqrt{16+36+4}}$

$d(P,\pi) = \cfrac{0}{\sqrt{56}}$

$\bm{d(P,\pi) = 0}$

点と平面の間の距離はゼロに等しいため、事実上、点は平面に属します。

演習 4

次の 2 つの平面間の距離を求めます。

$\pi_1 : \ 2x-y+5z-3=0 \qquad \qquad \pi_2 : \ 2x-y+5z-7=0$

解決策を参照

まず、2 つの平行な平面を扱っていることを確認する必要があります。 2 つの平面の方程式の係数は、独立項を除いてすべて比例するため、これらは実際に 2 つの平行な平面です。

$\cfrac{2}{2}=\cfrac{-1}{-1}=\cfrac{5}{5} \neq \cfrac{-3}{-7} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

この場合、係数 A、B、C が等しいため、2 つの平面間の距離を次の式で計算します。

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

したがって、値を式に代入して演算を実行します。

$d(P,\pi) = \cfrac{\lvert -7-3\rvert}{\sqrt{2^2+(-1)^2+5^2}}= \cfrac{\lvert -10\rvert}{\sqrt{30}} = \cfrac{\bm{10}}{\bm{\sqrt{30}}}$

演習 5

次の 2 つの平行な平面間の距離を求めます。

$\pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0$

解決策を参照

前景平面はパラメトリック方程式の形式で定義されるため、2 つの平行な平面間の距離の公式を適用するには、まずそれを一般方程式の形式に変換する必要があり、多くの計算と時間がかかります。したがって、その平面上の点を取得し、その点から他の平面までの距離を計算する方が高速です。

したがって、平面 π ₁が通過する点の座標は、各パラメトリック方程式の独立項に対応します。

$P(3,-2,5)$

ここで、次の式を適用して、この点と他の平面の間の距離を求めます。

$d(P,\pi_2) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

$d(P,\pi_2) = \cfrac{\lvert 3\cdot 3+2\cdot (-2)+(-2)\cdot 5-9\rvert}{\sqrt{3^2+2^2+(-2)^2}}$

$d(P,\pi_2) = \cfrac{\lvert 9-4-10-9\rvert}{\sqrt{9+4+4}}$

$d(P,\pi_2) = \cfrac{\lvert -14\rvert}{\sqrt{17}}$

$d(P,\pi_2) = \cfrac{14}{\sqrt{17}}$

したがって、2 つの平行な平面間の距離は次のようになります。

$\bm{d(\pi_1,\pi_2)=d(P,\pi_2) =} \cfrac{\bm{14}}{\bm{\sqrt{17}}}$

空間上の点から平面までの距離（式）

点から平面までの距離はどれくらいですか?

点から平面までの距離の公式

点から平面までの距離の計算例

2 つの平行な平面間の距離を計算します

2 つの平行な平面間の距離の計算例

点から平面までの距離の問題を解く

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする返信をキャンセル

点から平面までの距離はどれくらいですか?

点から平面までの距離の公式

点から平面までの距離の計算例

2 つの平行な平面間の距離を計算します

2 つの平行な平面間の距離の計算例

点から平面までの距離の問題を解く

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする 返信をキャンセル

コメントする返信をキャンセル