空間内の 2 つの線の相対位置

ここでは、空間 (R3) 内での 2 つの線の相対位置がすべてわかります。さらに、範囲による方法、または各線の点とベクトルからの 2 つの方法を使用して 2 つの線の間の相対位置を見つける方法についても説明します。例題や演習を段階的に解くこともできます。

空間内の 2 本の線の相対的な位置は何ですか?

解析幾何学では、3 次元空間 (R3) で作業する場合、2 つの線の間には 4 つの相対位置が考えられます。2 つの線は、結合線、平行線、割線、または割線になります。

平行線

2 本の線が同じ方向を向いていても共通点がない場合、その線は平行です。さらに、平行線は常に互いに同じ距離にあります。

一致する線

2 本の線が同じ方向を持っていて、さらにそれらのすべての点が共通している場合、2 本の線は一致します。

交差する線

交差する 2 つの線は方向が異なりますが、1 点で接触します。

交線

交差する 2 つの線は方向が異なり、どの点でも交差しません。したがって、2 つの交差した線は同じ平面上にありません。たとえば、線の上のグラフィック表現では、

$s$

常に列の先頭にいる

$r$

, したがって、彼らは決してお互いに触れることはありません。

2 つの直線の間の相対位置を知る方法は 2 つあります。これらは 2 つの直線の方程式の表現方法に依存します。

線がベクトル、パラメトリック、または連続方程式の形式である場合、点と各線のベクトルから相対位置を計算するのが最善です (この方法の説明は以下に示します)。
一方、直線が陰的な (または一般的な) 方程式の形式で定義されている場合、 2 つの行列のランクを計算することで 2 つの直線間の相対位置を知ることが容易になります (以下の説明を参照)。

点とベクトルから 2 つの直線の相対位置を求める

2 本の線の間にどのような相対位置があるかを、各線の点とベクトルで求めることができます。この方法は、直線がベクトル方程式、パラメトリック方程式、または連続方程式の形式で定義されている場合に使用するのに適しています。

したがって、方向ベクトルと 2 つの直線のそれぞれ上の任意の点を次のようにします。

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

したがって、2 つの線の相対位置を見つけるには、次の手順に従う必要があります。

‣最初に行う必要があるのは、2 つの直線のベクトルが比例しているかどうかを確認することであり、場合に応じて次のことを行います。

2 つのベクトルが比例する場合、線は平行または一致する可能性があります。したがって、一方の線の点がもう一方の線の方程式を満たすかどうかを確認する必要があります。
- 一方の線の点がもう一方の線の方程式を満たす場合、それは 2 つの線が一致することを意味します。
- それ以外の場合は、2 つの線が平行であることを意味します。
2 つのベクトルが比例していない場合、線が交差したり交差したりする可能性があります。この場合、次の 3×3 行列式を解く必要があります。

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- 前の行列式がゼロに等しい場合、2 つの直線は点で交差します (交差します)。
- 前の行列式がゼロ以外の場合、2 つの線は交差します。

次の図は、手順全体をまとめたものです。

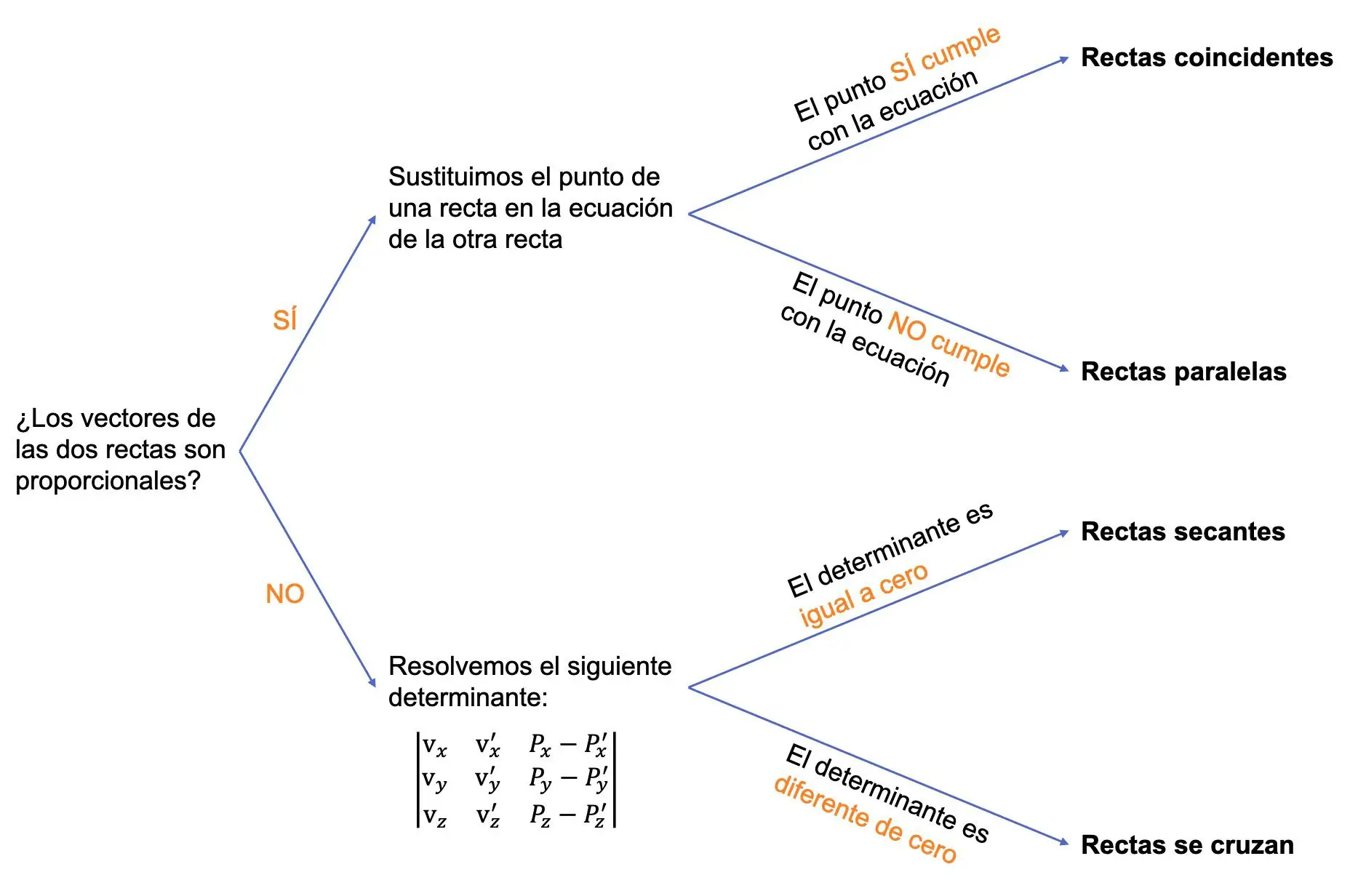
2 つの線の間の相対位置を決定する例

前の手順は少し複雑に見えるかもしれませんが、逆であることがわかるように、例として問題を解決します。

次の 2 つの行の間の相対位置を決定します。

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

2 つの直線はベクトル方程式として表現され、各直線の方向ベクトルは次のようになります。

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

そして、各線が通過する点は次のとおりです。

$R(2,0,1)\qquad \qquad S(1,-3,1)$

点と各線の方向ベクトルがわかったら、上記の方法を適用します。まず最初に、ベクトルの座標が比例しているかどうかを確認する必要があります。

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

2 つのベクトルは互いに比例しないため、線は互いに接触するか交差することしかできません。したがって、方向ベクトルと各直線上の点によって形成される次の行列式を解く必要があります。

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

値を式に代入します。

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

そして、行列式を計算します。これには、任意の方法 (Sarrus ルール、補数または余因子の方法など) を使用できます。

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

判定の結果がゼロであった場合、これは線が交差する（接触する）ことを意味する。しかし、行列式は 0 とは異なるため、線は交差します。

2行の相対位置を行ごとに求める

2 つの行の相対位置を見つけるもう 1 つの方法は、次に説明するように、2 つの具体的な行列のランクを計算することです。この方法は、2 つの直線が暗黙的な (または一般的な) 方程式形式である場合に非常に役立ちます。

したがって、3 次元空間 (R3) で暗黙的な (または一般的な) 方程式で表現された 2 つの直線があるとします。

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

A を 2 つのラインの係数で構成される行列とします。

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

そして、拡張行列 A’ を考えると、これは 2 行のすべてのパラメータによって形成される行列です。

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

次に、2 つの行の相対位置は、次の表に従って、前の 2 つの行列の範囲によって決定できます。

したがって、2 つの行間の相対位置を見つけるには、2 つの行列のランクを計算する必要があり、各行列のランクに応じてどちらかのケースになります。

この定理はルーシェ-フロベニウスの定理 (連立一次方程式を解くために使用される方法) を使用して証明できますが、非常に面倒であまり追加しないため、このページでは証明を行いません。

範囲によって 2 つの線の相対位置を求める方法の例

2 行間の相対位置に関する理論を行ごとに理解したら、例を通してそれがどのように実践されるかを見てみましょう。

次の 2 つの行の相対位置を見つけます。

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

2 つの直線は一般 (または暗黙的な) 方程式の形式になっているため、ランク法を使用して 2 つの直線間の相対位置を見つけます。したがって、行の係数を使用して行列 A と拡張行列 A’ を構築します。

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

両方の行列を取得したら、それぞれの順位を計算する必要があります。まず、行列式によって行列 A のランクを計算します。

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

行列 A には非ゼロ 3×3 部分行列の行列式が含まれているため、行列 A のランクは 3 になります。

次に、拡張行列 A’ の範囲を計算します。行列 A’ は常に少なくとも行列 A のランクにあり、この場合は 3 の価値があるため、ランク 4 であるかランク 3 であるかを確認するだけで十分です。これを行うには、行列式を解きます。 4x 行列 4 を加算 (または余因子) によって計算します。

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

拡張行列全体の行列式はゼロであるため、行列 A’ もランク 3 になります。

したがって、行列 A と行列 A’ はランク 3 であるため、 2 つの線は交差します。つまり、それらの間には交差点が 1 つだけあります。

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

上の表は、行列 A と A’ の範囲に応じた 2 つの線の間の相対位置の考えられるすべてのケースをまとめたものであることに注意してください。

空間内の 2 つの線の間の相対位置の問題を解決しました

演習 1

次の 2 つの行の間の相対位置を見つけます。

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

解決策を参照

両方の直線はベクトル方程式として表されるため、各直線の 1 点 1 ベクトル法から 2 つの直線間の相対位置を求めます。

各ラインの方向ベクトルは次のとおりです。

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

各行に属する点は次のとおりです。

$R(3,4,0)\qquad \qquad S(1,-2,2)$

したがって、この手順を適用するには、まず方向ベクトルの成分が比例しているかどうかを確認する必要があります。

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

2 つのベクトルは互いに比例しないため、線は交差または交差することしかできません。したがって、方向ベクトルと各直線上の点で構成される次の行列式を解く必要があります。

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

値を式に代入します。

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

そして行列式を計算します。

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

決定子の結果は 0 に等しいため、線は交差します。

演習 2

次の 2 つの行の相対位置を計算します。

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

解決策を参照

最初の行はパラメトリック方程式の形式で、2 行目は連続方程式の形式であり、これを使用して、各線の 1 点ベクトル法から 2 つの線の間の相対位置を決定します。

右の方向ベクトルの座標

$r$

パラメータの前の係数です

$t,$

と線の方向ベクトルの座標

$s$

は分母の数です。

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

各行に属する点は次のとおりです。

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

したがって、この手順を適用するには、まず方向ベクトルの成分が比例しているかどうかを確認する必要があります。

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

2 つのベクトルは互いに比例するため、線は平行または一致することしかありません。この疑念を取り除くには、線上の点を置き換える必要があります。

$r$

直線の方程式の中で

$s$

（またはその逆）上記の方程式を満たすかどうかを確認します。

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

線分の点を置き換えることによって等号が得られ、一方の線の点がもう一方の線の方程式を満たし、さらにそれらの方向ベクトルが比例します。したがって、 2 つの線は一致します。

演習 3

次の 2 つの行の相対位置を見つけます。

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

解決策を参照

2 つの直線は一般的な (または暗黙的な) 方程式形式であるため、ランク法を使用して 2 つの直線間の相対位置を見つけます。したがって、行の係数を使用して行列 A と拡張行列 A’ を作成します。

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

両方の行列を取得したら、それぞれの順位を計算する必要があります。まず、行列式によって行列 A のランクを計算します。

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

行列 A の 3×3 行列式はすべて 0 ですが、行列内に 0 以外の 2×2 行列式があるため、行列 A のランクは 2 になります。

次に、拡張行列 A’ の範囲を計算します。行列 A’ は常に少なくとも行列 A の範囲 (この場合は 2) になるため、相殺されない 3×3 行列式があるかどうか、また行列式がどの程度であるかを確認する必要があります。マトリックス全体:

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

拡張行列 A’ には確かに 3×3 の非ゼロ副行列式が含まれており、さらに、拡張行列全体の行列式は 0 に等しいため、行列 A’ のランクは 3 になります。

したがって、行列 A はランク 2 であり、行列 A’ はランク 3 であるため、 2 つの直線は平行になります。つまり、それらには何の共通点もありません。

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

方法の説明 (上記) では、行列 A と A’ のランクに応じた 2 つのライン間の相対位置の考えられるすべてのケースをまとめた表があることを思い出してください。

演習 4

次の 2 つの行の相対位置を見つけます。

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

解決策を参照

この場合、2 つの直線はデカルト (または暗黙的) 方程式形式であるため、順序付けメソッドを使用して 2 つの直線間の相対位置を見つけます。したがって、行の係数を使用して行列 A と拡張行列 A’ を構築します。

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

2 つの行列がわかったら、それぞれの順位を計算する必要があります。まず、行列式によって行列 A のランクを計算します。

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

行列 A には行列式が 0 以外の 3×3 部分行列が含まれているため、行列 A のランクは 3 になります。

次に、拡張行列 A’ の範囲を計算します。行列 A’ は常に行列 A のランク以上であり、この場合は 3 の価値があるため、ランク 4 であるかランク 3 であるかを確認するだけで十分です。これを行うには、次の行列式を解きます。加算 (または余因子) による 4×4 行列のセット:

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$