空間内の線から平面までの距離

ここでは、線から平面までの距離がどのように計算されるかがわかり、さらに、段階的に解決される例や演習を見ることができます。

線と平面の間の距離はどれくらいですか?

解析幾何学では、空間内の線と平面の間の距離は、これら 2 つの幾何学的要素間の相対位置によって決まります。

線分が平面に含まれている場合、または線分と平面が平行である場合、それらの間の距離はゼロになります。
線が面に平行な場合、線から面までの距離は、線上の任意の点を取得し、その点から面までの距離を計算することによって求められます。

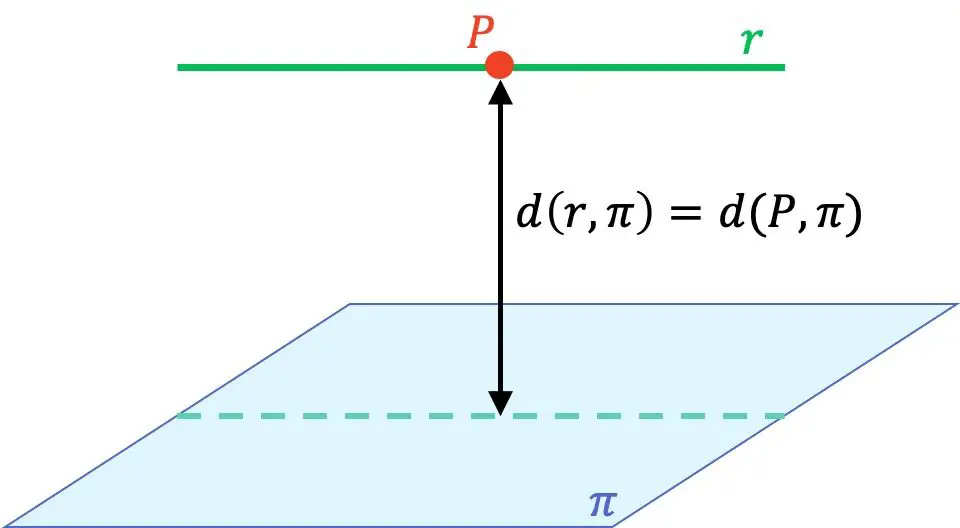
したがって、線から面までの距離を計算するには、線と面の間の相対位置を決定する方法と、点と面の間の距離を計算する方法を知っていることが不可欠です。したがって、公式が完全に理解できない場合、または公式がわからない場合は、最初にリンク先のページを参照することをお勧めします。そこには、説明、例、および解決済みの演習が段階的に掲載されています。

直線と平面間の距離の計算例

空間 (R3) 内の線と平面の間の距離を見つける方法を確認できるように、例として問題を解決します。

ラインはどのくらい離れていますか
$r$

飛行機の中

$\pi$

?

$\displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}$

$\pi : \ 4x+2y+z-6=0$

線と平面の間の距離を見つけるには、まず 2 つの間の相対位置を知る必要があります。

一方では、直線はパラメトリック方程式の形式で定義されるため、その方向ベクトルとそれが通過する点は次のようになります。

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}$

一方、平面に垂直なベクトルは次のようになります。

$\vv{n} =(4,2,1)$

したがって、平面と直線の間の相対位置を決定するには、直線の方向ベクトルと平面に垂直なベクトルの間のスカラー積を計算する必要があります。

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}$