ここでは、多項式、有理関数、指数関数、根付き関数、無限大の不定など、無限におけるあらゆる種類の極限を解く方法を示します。さらに、x の場合の極限について段階的に解決する 25 の練習問題でトレーニングすることができます。無限に向かう傾向があります。 。
x が無限大に近づく場合の関数の極限
x が infinity に近づくときの関数の極限は、正か負かに関係なく、実数値、プラス無限大、マイナス無限大、または存在しない値になる可能性があります。無限大での極限を解くには、x を無限大に置き換える必要があります。
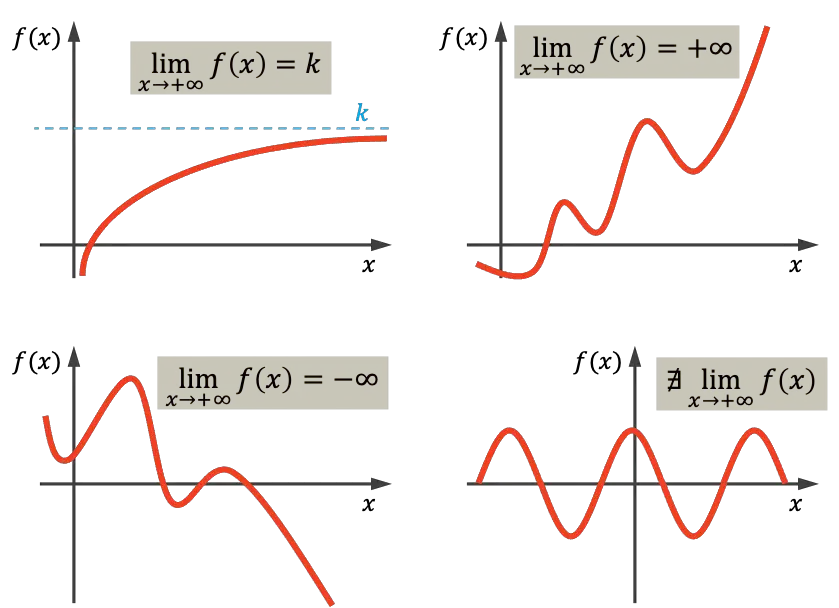
最初のグラフからわかるように、 xが大きくなるにつれて関数はkに近づくため、示されている関数は無限大に向かって実数値 kに近づく傾向があります。右上の関数は、 xの値が増加するにつれて無限に増大するため、 xが無限大に近づくにつれて無限大になる傾向があります。一方、左下のグラフは減少が止まらず、マイナス無限大に向かう傾向があります。最後に、最後の関数は周期的であり、どのような値にもなる傾向がないため、この場合は無限大の制限はありません。
無限遠の極限を解く方法
多項式関数の無限大への制限を解くには、関数の最高次項でのみ x を無限大に置き換える必要があります。
たとえば、最高次数の単項式に無限大のみを代入する、無限大への制限の次の計算を見てください。
![]()
この例でわかるように、非常に大きな数 (+∞) の 2 乗は常に非常に大きな数 (+∞) になるため、+∞ の 2 乗は +∞ になります。
そして、同じことが乗算でも起こります。非常に大きな数 (+∞) を乗算すると、常に非常に大きな数 (+∞) が得られます。例えば:
![]()
警告:無限の制限を計算するには、次の要素を考慮することが重要です。
→負の数を偶数乗すると正になります。したがって、マイナスの無限大を偶数乗すると、プラスの無限大が得られます。
![]()
→負の数を奇数乗したものは負です。したがって、マイナス無限大の奇数乗はマイナス無限大となります。
![]()
→負の数を乗算すると、無限大の符号が変わります。
![]()
→任意の数を割った値
![]()
0 を返します:
![]()
無限への制限の例
したがって、無限への制限が多項式でどのように解決されるかがわかります。以下に、解決されるそのような制限のいくつかを示します。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle \lim_{x \to +\infty} (x^3-x^2+4)= (+\infty) ^3 = \bm{+\infty}\\[4ex]\displaystyle\lim_{x \to +\infty} (-5x+2)= -5(+\infty)= \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^2-7x+1) = (-\infty)^2 = \bm{+\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^3-x^2+4)= (-\infty) ^3 = \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to +\infty} \ \cfrac{1}{x}= \cfrac{1}{+\infty} = \bm{0}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bbab608d243555490569fab22938c6e9_l3.png)
無限への未決定の限界
場合によっては、無限と無限の間の無限の不確定性、または無限から無限を引く不確定性が得られる場合があるため、無限の限界を計算するのは必ずしも簡単ではありません。
![]()
このタイプの不定形 (または不定形) を取得した場合、結果を直接知ることはできませんが、極限値を見つけるための予備手順を実行する必要があります。次に、無限遠における不定限界がどのように解決されるかを見ていきます。
無限の間の無限の不確定性
不確定性無限を無限で割った結果を求めるには、分数の分子の次数と分母の次数を比較する必要があります。
- 分子多項式の次数が分母多項式の次数より小さい場合、無限大にわたる無限不確定性はゼロに等しくなります。
- 分子多項式の次数が分母多項式の次数と等しい場合、無限大にわたる無限不確定性は 2 つの多項式の主係数の商になります。
- 分子多項式の次数が分母多項式の次数より大きい場合、無限大間の無限不確定性により、多かれ少なかれ無限大が得られます (符号は 2 つの多項式の主項に依存します)。
![\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”></p>
</p>
<p>たとえば、次の極限では、分子多項式は 2 次であり、分母多項式は 3 次であるため、極限の解は 0 になります。</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c969e4b99985b44006e57d554ff0247_l3.png)
![]()
この別の例を見てください。この例では、有理関数の 2 つの多項式は 2 次であるため、無限大での極限を計算するには、より高次の項の係数を除算する必要があります。
![]()
最後に、次の極限では、分子の関数の次数が分母の関数より大きいため、無限大における無限大の不確定性により無限大が得られます。さらに、分子からは正の無限大が得られますが、分母からは負の無限大が得られるため、極限の結果は負になります (負と負の間の正は負です)。
![]()
無限と根の間の無限不確定性
一方、無理関数(根のある関数)の次数は、主項の次数と根号の指数との商になります。
![Rendered by QuickLaTeX.com \sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffc00917d2cc316211a57feafdddd0d2_l3.png)
したがって、根を持つ関数の極限によって infinity 間の無限の不確定性が生じる場合、分子と分母の次数に関して上で説明したのと同じルールを適用する必要がありますが、根を持つ多項式の次数は異なる方法で計算されることを考慮に入れてください。
根号を使用した関数の無限制限の次の例を見てください。
![]()
分子の次数は 2、分母の次数は 4 (8/2=4) であり、分子の次数が分母の次数より小さいため、制限は 0 になります。
無限と指数関数間の無限不確定性
指数関数の増加は多項式関数の増加よりもはるかに大きいため、指数関数の次数が多項式関数の次数よりも大きいことを考慮する必要があります。
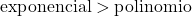
![]()
この例では、分母は指数関数から形成されているため、分子よりも高次になります。したがって、無限大の間の不定形無限は 0 になります。
無限マイナス無限不確定性
無限マイナス無限の不確定性を解くかどうかは、関数に分数があるか根があるかによって異なります。それでは、これら 2 つの異なるケースについて、このタイプの不確定性を解決する方法を見てみましょう。
分数を伴う不確定性無限マイナス無限
代数分数の加算または減算で無限マイナス無限の不確定性が発生する場合、最初に分数の加算または減算を行ってから、極限を計算する必要があります。
例を段階的に解決して、分数を含む関数の不確定性無限大マイナス無限大を計算する方法を見てみましょう。
![]()
まず、制限を計算してみます。
![]()
しかし、不確定性 ∞-∞ が得られます。
まず分数を減算する必要があります。これを行うには、分数を共通の分母に換算します。つまり、一方の分数の分子と分母に、もう一方の分数の分母を掛けます。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68e489c5833478cb20929ea07ae2971d_l3.png)
2 つの分数の分母が同じになったので、これらを 1 つの分数に結合できます。
![]()
分子と分母を演算します。
![]()
そして最後に、制限を再度計算します。
![]()
この場合、分子の次数が分母の次数よりも大きいため、無限大間の無限不確定性は + ∞ を与えます。
根を持つ不確定性無限マイナス無限
根号加算または根号減算で無限マイナス無限不確定性が発生する場合、まず関数を共役根号式で乗算および除算してから、極限を解く必要があります。
ステップバイステップの例に従って、無理関数の不確定性無限マイナス無限を解決する方法を見てみましょう。
![]()
まず、根号を使用して関数の極限を解いてみます。
![]()
ただし、不定形 ∞-∞ が得られます。したがって、無限から無限を引いた不確定性がどの程度かを知るには、説明した手順を適用する必要があります。
関数には根号があるため、共役無理数式で関数全体を乗算および除算します。
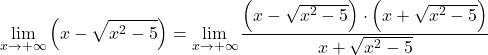
分子の代数式は、和と差の積の注目すべき単位に対応するため、式を簡略化できます。
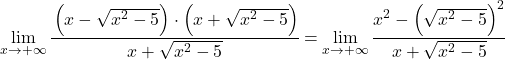
次に、制限の根が二乗されるので、これを単純化します。
![]()
分数の分子を演算します。
![]()
![]()
そして最後に、制限の計算をやり直します。
![]()
したがって、無限大で割った数値はゼロに等しいため、制限の結果は 0 になります。
無限遠の制限に関する演習を解決しました
演習 1
グラフ関数の次の限界を求めます。
![]()
![]()
![]()
![]()
![]()
![]()
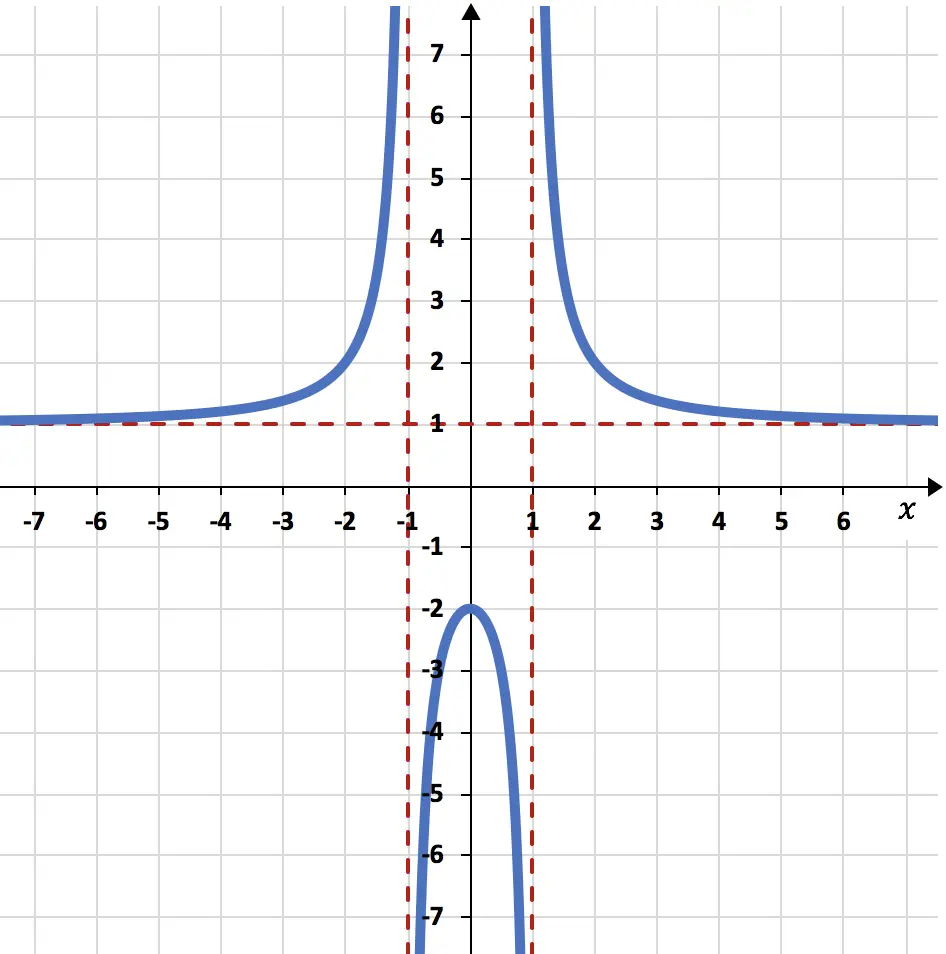
x がマイナス無限大およびプラス無限大に向かう傾向がある場合の関数の極限は 1 になります。
![]()
![]()
点 x=-1 における関数の左側と右側の横方向の限界は、それぞれプラスの無限大とマイナスの無限大です。
![]()
![]()
最後に、x が 1 になる傾向があるときの関数の横方向の限界は、マイナス無限大とプラス無限大に値します。
![]()
![]()
演習 2
x が次の関数の無限大に近づくときの極限を解きます。
![]()
無限大での極限を解くには、多項式の最高次項の x を無限大に置き換える必要があります。
![]()
演習 3
次の多項式関数の無限大の極限を計算します。
![]()
無限大での極限を解くには、多項式の最高次項の x を無限大に置き換えて計算を実行します。
![]()
演習 4
次の多項式関数の少なくとも無限の極限を解きます。
![]()
無限大での極限を計算するには、多項式の最高次項の x をマイナス無限大に置き換え、関数を評価します。
![]()
マイナス無限大を二乗するので、無限大の符号はプラスになります。
演習 5
次の有理関数の無限遠の極限を求めます。
![]()
無限への制限を決定するには、分数の分子と分母の最高次数の項で x をプラス無限大に置き換えます。
![]()
プラスまたはマイナスの無限大で割った数値は 0 に等しいことに注意してください。
演習 6
次の極限を無限大で解きます。
![]()
x が関数の ±∞ に向かう傾向がある場合の極限を計算するには、関数の最高次数の単項式を調べるだけです。
![]()
演習 7
x が負の無限大に近づくときの次の関数の極限を計算します。
![]()
この場合、二次項を無限大に置き換えるだけで十分です。
![]()
演習 8
x が無限大に近づくときの次の指数関数の極限を求めます。
![]()
これは指数関数ですが、極限を解くプロセスは同じです。つまり、x を無限大に置き換えます。
![]()
演習 9
次の指数関数の無限極限を解きます。
![]()
この制限を解決するには、分数のプロパティを使用する必要があります。
![]()
演習 10
次の極限を無限大で解きます。
![]()
この制限により、プラス無限大の間に不確定マイナス無限大が生じます。分子の次数は分母の次数より大きいため、不定極限はプラス無限大に等しくなります。ただし、除算は負の無限大と正の無限大であるため、結果は負の無限大になります。
![]()
演習 11
次の不確定な制限を修正します。
![]()
この問題では、無限大に対する不定形式の無限大は、同じ次数の 2 つの多項式の商から得られるため、不定極限の結果は、それらの主係数の除算になります。
![]()
演習 12
次の制限を少なくとも無限大まで計算します。
![]()
分子の代数表現の次数は分母の表現の次数より小さいため、不確定性 +∞/+∞ は 0 を返します。
![]()
演習 13
ルートを使用して、次の関数の不定極限を解きます。
![]()
分子の式は根号の下にあるため、次数は 7/3 です。一方、分母多項式は 2 次です。そして、7/3>2 であるため、この制限によりさらに無限大が得られます。
![]()
演習 14
次の関数の無限極限を分数で求めます。
![]()
この演習では、分子の次数が分母の次数より大きい、不確定性マイナス無限大をマイナス無限大で割った値を取得します。したがって、次のようになります。
![]()
演習 15
次の関数の少なくとも無限の極限を求めます。
![]()
分母多項式は 2 次であり、分子多項式は 1 次です。したがって、無限不確定性を無限で割ると 0 になります。
![]()
演習 16
次の関数の少なくとも無限の極限を解きます。
![]()
分子は分母より 1 度大きいため、不定形 ∞/∞ の結果は無限大になります。さらに、負の間の正は負に変換されるため、無限大記号は負になります。
![]()
演習 17
次の極限を無限大で解きます。
![]()
指数関数は多項式関数より高次であるため、極限は無限大になります。ただし、正を負で割ると、無限大の符号は負になります。
![]()
演習 18
次の関数の無限極限を平方根で計算します。
![]()
分子は平方根で構成されているため、次数は 2/2=1 になります。この場合、分子の次数は分母の次数と等しいため、無限大間の無限不確定性は次のように解決されます。
![]()
演習 19
2 つの根号を使用して次の関数の無限極限を解きます。
![]()
分子の次数は 7/3 = 2.33、分母の次数は 5/2 = 2.5 です。したがって、分子の次数が分母の次数より小さいため、無限の間の不定無限極限は 0 になります。
![Rendered by QuickLaTeX.com \displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-681401701d7d7f3fad1879db26659942_l3.png)
演習 20
次の制限を計算します。
![]()
分子の次数に関係なく、分母に指数関数があるため、無限大に対する不定形無限の結果は 0 になります。
![]()
演習 21
次の有理関数の無限極限を決定します。
![]()
まず、関数に無限大を代入して制限を計算してみます。
![]()
しかし、不確定性 ∞ – ∞ がわかります。したがって、分数を共通の分母に換算します。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7e2820674bc86d085f6deec7fdf9adf8_l3.png)
2 つの分数の分母が同じになったので、これらを 1 つの分数に結合できます。
![]()
分子のかっこを作ります。
![]()
そして最後に、制限を決定します。
![]()
この場合、分子の次数が分母の次数よりも大きいため、不決定 ∞/∞ は +∞ を与えます。
演習 22
x が 0 に近づくにつれて、次の分数関数の極限を解きます。
![]()
まず、いつものように制限を計算してみます。
![]()
しかし、不定形 ∞-∞ が得られます。したがって、関数の分数を共通の分母に減らす必要があります。
この場合、 x 4は x 2の倍数であるため、2 番目の分数の分子と分母に x 2を掛けるだけで、両方の分数が同じ分母を持つことが保証されます。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-876115dc1fb49e81373d70be5fdcfb5e_l3.png)
2 つの分数を引き算できるようになりました。
![]()
もう一度制限を解決してみます。
![]()
しかし、最終的にはゼロから始まる定数の不確定性が生じます。したがって、関数の横方向の限界を計算する必要があります。
![]()
![]()
結論として、点 x=0 における関数の 2 つの横方向の極限は -∞ を与えるため、極限の解は -∞ になります。
![]()
演習 23
次の関数の無限極限をルートで解きます。
![]()
極限を解こうとすると、無限大から無限大を引いた不確定性が得られます。
![]()
したがって、関数には根号があるため、共役根号式で乗算および除算する必要があります。
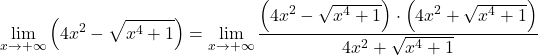
分子には、和と差の注目すべき積があり、これは二乗の差に等しいです。まだ:
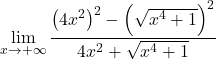
根号を二乗に単純化します。
![]()
分子を操作します。
![]()
![]()
そして最後に限界を見つけます。
![]()
この場合、分子の次数が分母の次数よりも大きいため、不確定性無限大を無限大で割った値はより無限大になります (平方根によって次数が 2 減少することを思い出してください:
![]()
)。
演習 24
次の無理関数の x が無限大に近づくときの極限を解きます。
![]()
まず、いつものように制限を計算してみます。
![]()
しかし、これでは無限大の差が不定になってしまいます。したがって、関数にはルートがあるため、共役根号で式を乗算および除算する必要があります。
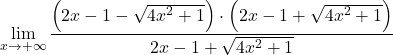
分数の分子の注目すべき等価性をグループ化します。
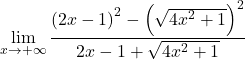
平方根を解きます。
![]()
差の二乗の注目すべき恒等式を解決します。
![]()
分子を操作します。
![]()
![]()
そして最後に、無限大での制限値を計算します。
![]()
分母に x の 2 乗がありますが、根の中にあるため、その次数は実際には 1 です。
![]()
したがって、分子の次数は分母の次数と同じであるため、不確定性 -∞/+∞ の結果は、最高次数の x の係数の除算になります。
![]()
分母に 2 つの 1 次項があることに注意してください。
![]()
そして
![]()
、不確定性 -∞/+∞ を解決するには、1 次項のすべての係数を取得する必要があります。
![]()
の
![]()
そしてその
![]()
の
![]()
演習 25
分数を使用して、x が次の関数の 1 に近づくときの極限を計算します。
![]()
極限を試行すると、無限から無限を引く不定の極限が得られます。
![]()
したがって、分数を共通の分母に減らす必要があります。つまり、一方の分数の分子と分母に、もう一方の分数の分母を乗算する必要があります。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-75bf3ffa177f32711c5509ce5fe5992d_l3.png)
2 つの分数の分母は同じなので、次のようにまとめることができます。
![]()
私たちは以下を運営しています:
![]()
![]()
そして、もう一度制限を解いてみます。
![]()
しかし、不確定性ゼロがゼロで除算されることがわかります。したがって、分子と分母の多項式を因数分解する必要があります。
![]()
ここで、分子と分母で繰り返される因数を削除して分数を単純化します。
![]()
そして最後に、制限を解決します。
![]()