減算の導関数

9月 17, 2023

この記事では関数の引き算（公式）の求め方を解説します。また、減算導関数の例や、段階的に解決された練習問題も見つかります。

減算の導関数の公式

2 つの関数を減算した導関数は、各関数の導関数を個別に減算したことと同じです。

$z(x)=f(x)-g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)-g'(x)$

言い換えれば、2 つの関数を個別に微分してから減算することは、最初に関数を減算してから導関数を求めることと同じです。

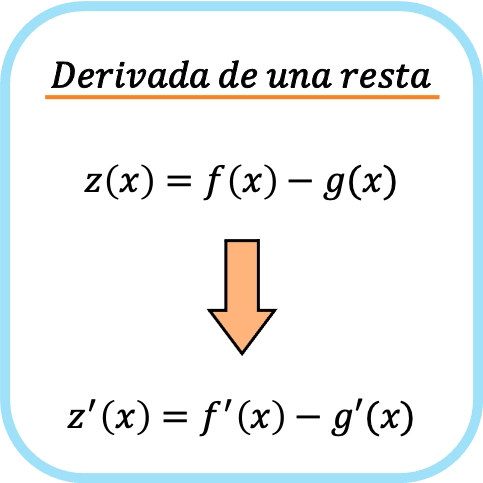
減算の導関数

同様に、同じ微分規則が 2 つ以上の関数の減算にも適用されるため、3、4、5、… 関数の減算がある場合は、それぞれを個別に微分してから減算する必要があります。

$\begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}$

ご覧のとおり、関数の差の導関数の公式は、和の導関数の規則と非常によく似ています。

➤ 「関数の和の導関数」を参照

減算の導関数の例

減算の導関数の公式が何であるかを理解したら、次にこのタイプの演算の導関数の例をいくつか分析して、関数の減算がどのように導出されるかを完全に理解します。

例 1: ポテンシャル関数の減算の導関数

$f(x)=x^3-4x$

2 つの関数を減算した導関数は、各関数の導関数を個別に差分したものと等価です。したがって、最初に各関数の導関数を個別に計算します。

$\cfrac{d}{dx} \ x^3=3x^2$

$\cfrac{d}{dx}\ 4x=4$

したがって、関数全体の導関数は次のようになります。

$f'(x)=3x^2-4$

例 2: さまざまな関数の減算の導関数

$f(x)=\text{cos}(x)-\log_7(x^2)$

減算関数を区別するには、まず 2 つの関数を個別に微分してから、それらを減算する必要があります。

$\cfrac{d}{dx} \ \text{cos}(x)=-\text{sen}(x)$

$\cfrac{d}{dx}\ \log_7 (x^2)=\cfrac{2x}{x^2\cdot \ln(7)}=\cfrac{2}{x\ln(7)}$

そして、2 つの導関数を作成した後、同じ初期順序でそれらを減算します。

$f'(x)=-\text{sen}(x)-\cfrac{2}{x\ln(7)}$

例 3: 2 乗減算の導関数

$f(x)=\left(x^7-2x^3-9\right)^2$

この場合、これは 3 つの 2 乗関数間の減算であるため、複合関数になります。したがって、ポテンシャル関数の導関数の公式と連鎖規則を使用して、関数全体の導関数を計算する必要があります。

$f(x)=2\left(x^7-2x^3-9\right)\cdot \left(7x^6-6x^2\right)$

➤参照: べき乗の導関数の公式

減算の微分に関する演習を解決しました

次の関数の減算を導き出します。

$\text{A) } f(x)=9x^3-5x$

$\text{B) } f(x)=4x^5-6x^4-x^2-4$

$\text{C) } f(x)=\left(-3x^7-2x^5\right)^4$

$\text{D) } f(x)=\ln(5x^2+3x)-\text{cos}(x)$

$\text{E) } f(x)=8x^3-e^{5x}-\sqrt{8x+2}$

解決策を見る

$\text{A) } f'(x)=27x^2-5$

$\text{B) } f'(x)=20x^4-24x^3-2x$

$\text{C) } f'(x)=4\left(-3x^7-2x^5\right)^3\cdot (-21x^6-10x^4)$

$\text{D) } f'(x)=\cfrac{10x+3}{5x^2+3x}-\bilg(-\text{sen}(x)\bigr)=\cfrac{10x+3}{5x^2+3x}+\text{sen}(x)$

$\text{E) } f'(x)=24x^2-5e^{5x}-\cfrac{8}{2\sqrt{8x+2}}=24x^2-5e^{5x}-\cfrac{4}{\sqrt{8x+2}}$

減算の導関数の証明

次に、導関数の定義から関数を減算する導関数の公式を示します。これは次のとおりです。

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

したがって、z が 2 つの異なる関数の差である場合:

$z(x)=f(x)-g(x)$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{z(x+h)-z(x)}{h}$

z を、極限式の関数の減算で置き換えます。

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)-g(x+h)\bigr]-\bigl[f(x)-g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-g(x+h)-f(x)+g(x)}{h}$

ここで、分数を分離し、2 つの分数の減算を求める変換を実行します。

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}+\frac{-g(x+h)+g(x)}{h}\right]$

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}-\frac{g(x+h)-g(x)}{h}\right]$

限界の法則を適用すると、上記の式を 2 つの異なる限界に分けることができます。減算の限界は限界の減算に等しいため、次のようになります。

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}-\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

よく見ると、各極限は関数の導関数に対応しています。これは、差の導関数の公式が満たされていることを意味します。

$\displaystyle z'(x)=f'(x)-g'(x)$

コメントする返信をキャンセル