ここでは、連鎖ルールとは何か、連鎖ルールを使用して関数を導出する方法を学びます。さらに、連鎖ルールを使用して解かれた導関数の例をいくつか見ることができ、連鎖ルールを適用して導関数を段階的に解く演習を行うこともできます。
連鎖の法則とは何ですか?
連鎖律は、複合関数を導出するために使用される公式です。連鎖則では、複合関数f(g(x))の微分値は、微分値f'(g(x))に微分値g'(x)を乗算したものに等しいと規定されています。
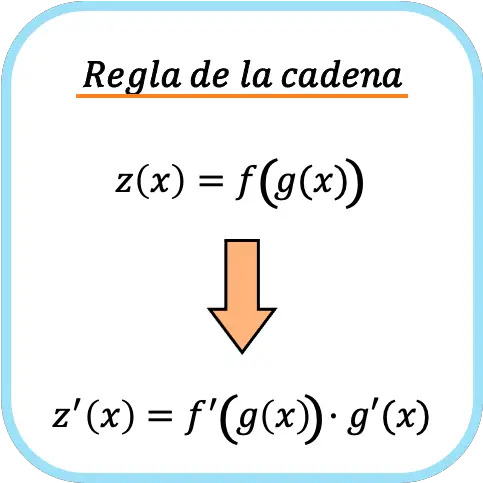
➤参照: 複合関数
非公式には、連鎖規則とは、関数を微分し、その関数に含まれるものを掛けることであると言われることがよくあります。
連鎖則の公式を使用すると、複合関数をはるかに簡単に微分することができます。これは、導関数の定義の制限を使用して関数の合成を微分する場合、多くの計算を実行する必要があるためです。
一方、このルールは複合関数の導関数を見つけるためにのみ使用され、あらゆる種類の関数や関数を使用した演算には使用されないことに注意する必要があります。たとえば、非常によくある間違いは、それを間違えて、次のような機能製品に連鎖ルールを適用することです。
![]()
❌
連鎖ルールは、ある関数の中に別の関数がある場合にのみ使用できます。
![]()
✅
連鎖律による導関数の例
連鎖ルールの定義を考慮して、連鎖ルールを例としていくつかの関数を導き出します。例の中で、連鎖ルールを使用して関数がどのように導出されるのか理解できない場合は、コメントで質問してください。
例1
この例では、連鎖則を使用して x の 2 乗の自然対数を導出します。
![]()
自然対数の導関数はその引数の 1 倍に等しいため、導関数は
![]()
なれ:
![]()
![]()
一方、x の 2 乗導関数は 2x です。
![]()
最後に、連鎖則を適用して関数全体の導関数を計算します。複合関数の導関数は、先ほど見つけた 2 つの導関数の積になります。
![]()
![]()
例 2
この 2 番目の例では、多項式に基づいてポテンシャル関数を導出します。
![]()
べき乗を導出するには、元の指数をその前に置き、指数から 1 単位を減算する必要があるため、連鎖ルールを適用しないポテンシャル関数の導関数は次のようになります。
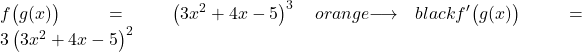
ここで、括弧内にあるものを推測します。
![]()
最後に、連鎖則を使用して関数全体の導関数を解きます。これは、前に計算した 2 つの導関数の乗算になります。
![]()
![]()
例 3
この場合、x の 3 乗と 7x の正弦導関数を解きます。
![]()
実際、これは関数の合成です。サイン関数内に関数 x 3 +7x があるため、連鎖則を使用して合成関数の導関数を見つけることができます。
一方では、サインの導関数はコサインであるため、外部関数の導関数はサインと同じ引数を持つコサインになります。
![]()
一方、x 3 +7x の導関数は 3x 2 +7 です。
![]()
したがって、複合関数の導関数は、次の 2 つの導関数の積になります。
![]()
![]()
連鎖ルールを使用した導関数に関する演習を解決しました
演習 1
連鎖ルールを使用して次の複合関数を導出します。
![]()
外部関数はポテンシャル関数であるため、その導関数を計算するには、次の式を適用する必要があります。
![]()
![]()
そして、内部の関数の導関数を計算します。これはべき乗の減算であるため、導関数を計算するには、次の式を各項に適用する必要があります。
![]()
![]()
![]()
つまり、複合関数の導関数は、次の 2 つの導関数の積です。
![]()
![]()
演習 2
連鎖則を使用して、次の複合関数の導関数を解きます。
![]()
まず、外部関数の導関数を求めます。
![Rendered by QuickLaTeX.com \begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e5d21c7196c7ebaeaf6ca11762ca251_l3.png)
そして今度は内部関数の導関数を解きます。
![]()
したがって、関数全体の導関数は次のようになります。
![]()
![]()
演習 3
連鎖則を使用して、次の関数の構成の導関数を計算します。
![]()
これは指数関数であるため、導関数を計算するには、次の式を適用する必要があります。
![]()
![]()
また、関数と関数の指数も区別します。
![]()
そして、連鎖規則を使用して、整数複合関数の導関数を求めます。
![]()
![]()
演習 4
連鎖律を使用して、次の複合関数の導関数を求めます。
![]()
無理関数の引数に正弦関数と線形関数があるので、これは関数の合成です。したがって、最初にルートの導関数を計算します。
![]()
![Rendered by QuickLaTeX.com f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e909efbe50930f94cce0b2485b060046_l3.png)
そして今、ラジカルから議論を導き出します。これは関数の合計であるため、導関数は各項の導関数の合計になります。
![]()
したがって、関数全体の導関数は、計算された 2 つの導関数の乗算に等しくなります。
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fad132b49a5faab86a3955efd5422973_l3.png)
演習 5
連鎖規則を使用して、次の関数の構成を導出します。
![]()
連鎖則を適用するには、べき乗と多項式の導関数を求め、それらを乗算する必要があります。したがって、対応する式を使用して電力を導き出します。
![]()
![]()
次に、指数から多項式関数を導出します。
![]()
そして連鎖律は、関数全体の導関数が、今見つけた導関数の積であることを示しています。
![]()
![]()
演習 6
![]()
自然対数の引数には 2 つの異なるタイプの関数の積があるため、この問題の関数は明らかに合成です。そこで、まず対数を微分します。
![]()
![]()
次に、対数引数から関数を導出します。これは 2 つの関数の乗算であるため、導出するには次の式を使用する必要があります。
![]()
![Rendered by QuickLaTeX.com \begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-643ddf7ec82cbcc3bc685ceadf59da98_l3.png)
したがって、関数全体の導関数は、連鎖則に従って、次の 2 つの導関数の積になります。
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6912d0951fb85a61df21cbed282000f2_l3.png)
演習 7
連鎖律を使用して次の関数の導関数を解きます。
![]()
これは関数の合成なので、対数とその引数を別々に微分し、導関数を掛けます。
したがって、まず、対数を底 9 で微分します。
![]()
![]()
次に、対数の引数の導関数を計算します。数値 e の引数には関数が含まれていることに注意してください。つまり、それは複合関数であるため、この関数を導出するには連鎖規則も適用する必要があります。
![]()
![]()
したがって、対数の整数引数の導関数は次のようになります。
![]()
そして最後に、関数全体の導関数は f'(g(x)) と g'(x) の積になります。
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a702df902c9f1eff66e14836a262c0a_l3.png)
演習 8
連鎖ルールを使用して次の複合関数を導出します。
![]()
この演習では複数の関数を構成しているため、連鎖ルールを数回適用する必要があります。まず、サインから三角関数を導出します。その導関数はコサインです。
![]()
次に、連鎖則を使用して正弦引数の導関数を計算します。
![]()
![Rendered by QuickLaTeX.com \begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e1c2492990456e277e493c898cb3924_l3.png)
最後に、連鎖規則を再度適用して、関数の構成全体の導関数を取得します。
![]()
![]()
チェーンルールの証明
最後に連鎖則の公式を証明します。これを行うには、導関数の数学的定義から始めます。
![]()
z を2 つの関数で構成される関数とします。
![]()
この場合、定義を適用した関数zの導関数は次のようになります。
![]()
すでにご存知のとおり、同じ項で分数の乗算と除算を行っても結果は変わりません。したがって、次のステップに進むことができます。
![]()
分数の分母を並べ替えます。
![]()
限界の特性を適用すると、上記の限界を 2 つに分割できます。積の限界は限界の積に等しいため、次のようになります。
![]()
そして、この式は次と同等です。
![]()
したがって、連鎖則の公式は導関数の定義から導かれたので証明されます。