このページでは、正方行列とは何かを説明し、正方行列の例を示します。さらに、正方行列が持つ特性、正方行列で実行できる演算、および存在するさまざまなタイプについても説明します。
正方行列とは何ですか?
正方行列とは、 行と列の数が同じ行列。
正方行列の例
次数 2 の正方行列
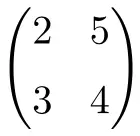
次数 3 の正方行列
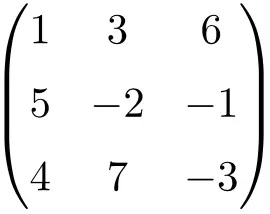
次数 4 の正方行列
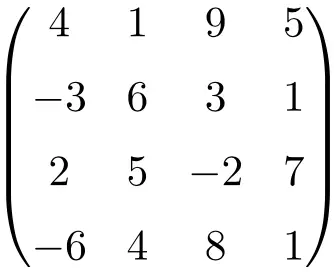
ご覧のとおり、正方行列は通常、次数によって名前が付けられます。つまり、次数 2 の正方行列は、次元 2×2 (2 行 2 列) の行列であることを意味します。または、次数 3 の正方行列について話します。これは、サイズが 3×3 (3 行 3 列) であることを示します。
正方行列の対角線
正方行列の対角線には特定の名前があり、主対角線と副対角線があります。
- 正方行列の主対角は、左上隅から右下隅までの要素で構成されます。

- 正方行列の二次対角は、左下隅から右上隅に向かう要素に対応します。

正方行列の性質
正方行列は線形代数で広く使用されているため、非常に重要です。それでは、このクラスの行列を非常に重要なものにする特徴は何なのかを見てみましょう。
- 任意の正方行列は、対称行列と非対称行列の和に分解できます。
- 2 つの正方行列が同じ次数であれば、相互に加算または減算できます。
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cec5286f22acdb6c84e876264157a89_l3.png)
- 2 つの正方行列は、可能な両方向に乗算できます。ただし、正方行列の積は可換ではありません。つまり、どちらの辺を掛けるかによって乗算結果が変わります。次の例では、結果が行列の位置にどのように依存するかに注目してください。
![Rendered by QuickLaTeX.com \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bdc76d296851b4ea7aa79124a026a01_l3.png)
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6405df17f38fb056fe7e5ab9e218f960_l3.png)
- 行列式を計算できるのは正方行列だけです。したがって、行列式は正方行列の場合にのみ解くことができます。たとえば、3×3 正方行列の行列式を求めるには、Sarrus の法則を適用する必要があります。
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6da09d0b791b047beec0aa2f3da1825_l3.png)
また、行列の行列式が 0 以外の場合、それは正則行列、つまり可逆であることを意味します。一方、行列式がゼロの場合、それは特異行列(逆行列を持たない) になります。
- 最後に、正方行列を対角化できます。したがって、基数の変更を実行して、正方行列の固有値 (または固有値) と固有ベクトル (または固有ベクトル) を計算できます。
正方行列の演算
これまで見てきたように、行列の行列式は行列が正方形の場合にのみ計算できます。同様に、行列が正方次元の場合にのみ実行できる特定の演算もあります。
マトリックスの跡
行列のトレースは、正方行列の主対角を形成する要素の合計です。
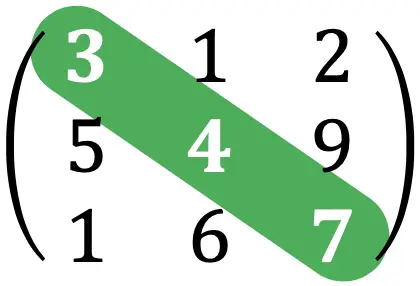
たとえば、上記の演習で得られた行列のトレースは次のようになります。
![]()
角型の種類
これで、存在する最も重要なタイプの正方行列が得られます。ダイのタイプをクリックして、その特徴を確認してください。

対称行列
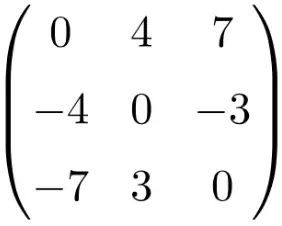
非対称行列
ご覧のとおり、正方行列には多くの種類があり、それぞれに異なる理由で独自の名前が付けられています。


