ここでは、楕円の方程式(公式)が原点を中心とするかどうか、どのように計算されるかを説明します。また、楕円の要素が何であるか、それらの計算方法、およびそれらが何に使用されるかについても説明します。さらに、楕円方程式の例と解答済みの演習を見ることができます。
楕円方程式の公式
デカルト座標での楕円の方程式の公式は次のとおりです。
![]()
金:
-

そして

は楕円の中心の座標です。
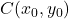
-

は楕円の水平方向の半径です。
-

は楕円の垂直半径です。
原点を中心とする楕円の方程式
非常に一般的なタイプの楕円は、中心が座標の原点、つまり点 (0,0) にあるものです。このため、原点を中心とする楕円の方程式を見つける方法を見ていきます。
楕円方程式の公式に従うと、次のようになります。
![]()
楕円の中心が座標の原点にある場合、これは次のことを意味します。
![]()
そして
![]()
は 0 に等しいため、方程式は次のようになります。
![]()
この式を楕円の正準方程式または縮小方程式と呼ぶ数学者もいます。
楕円の要素
楕円の方程式がどのようになるかを確認すると、その要素が何であるかがわかります。しかしその前に、楕円とは正確には何なのかを思い出してみましょう。
楕円は円周に非常によく似た平らで閉じた曲線ですが、その形状はより楕円形です。特に、楕円は、他の 2 つの固定点 (焦点 F および F’ と呼ばれる) までの距離の合計が一定である平面のすべての点の軌跡です。
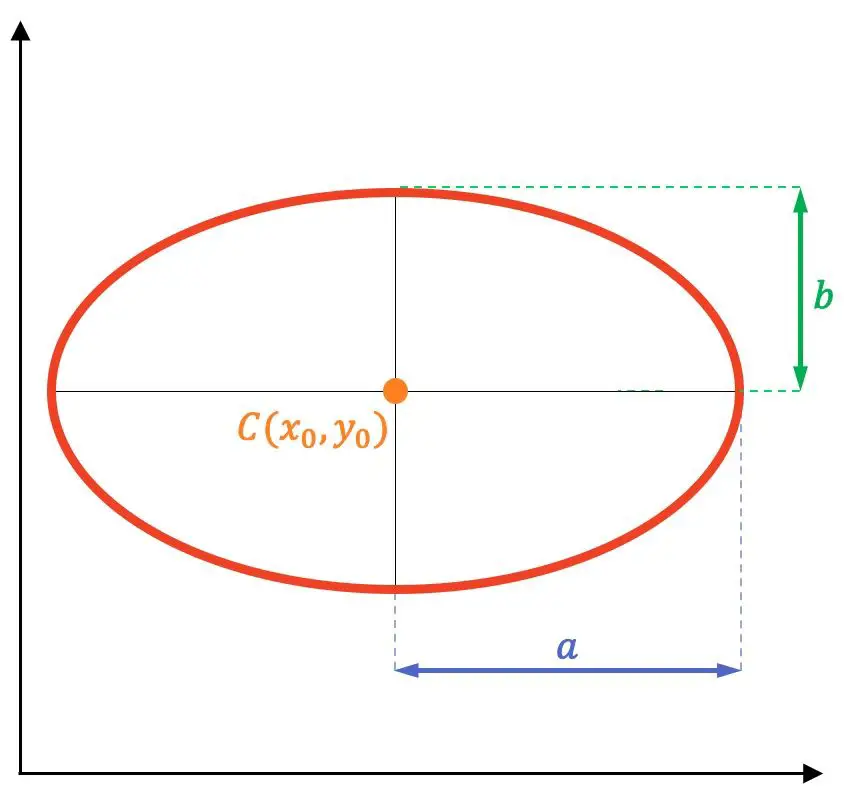
したがって、楕円の要素は次のとおりです。
- 焦点: これらは固定点 F および F’ (下の画像の紫色の点) です。楕円上の任意の点と各焦点の間の距離の合計は、楕円上のすべての点で一定です。
- 主軸または焦点軸: これは、焦点が位置する楕円の対称軸です。長軸とも呼ばれます。
- 二次軸: これは、主軸に垂直な楕円の対称軸です。これは短軸とも呼ばれ、焦点を結ぶセグメントの垂直二等分線に対応します。
- 中心: 楕円の軸の交点です。さらに、それは楕円の対称の中心です (グラフ上のオレンジ色の点)。
- 頂点: 楕円とその対称軸の交点 (黒い点)。
- 長半径または主軸:楕円の中心から主軸の頂点までの線分。
- 準短軸または二次軸:楕円の中心と二次軸の頂点の間のセグメント。
- 焦点距離: 2 つの焦点間の距離です。
- 半焦点距離: 中心と各焦点の間の距離に相当します。
- 無線ベクトル: は、楕円の任意の点を各焦点に結合するセグメント (グラフ内の青いセグメント) です。

楕円の要素間の関係
楕円のさまざまな要素は相互にリンクされています。さらに、それらの間の関係は、通常、楕円上の問題を解決し、方程式を決定するために必要となるため、楕円に関する演習では非常に重要です。
上の楕円の定義で見たように、楕円上の任意の点から焦点 F までの距離と、同じ点から焦点 F’ までの距離を足したものは一定です。この定数値は、長半径の測定値の 2 倍に等しいです。言い換えれば、楕円上の任意の点に対して次の等式が成り立ちます。
![]()
金
![]()
そして
![]()
は点 P から焦点 F および F’ までの距離です。
![]()
半焦点軸の長さです。
したがって、二次軸の頂点は焦点軸のちょうど中央にあるため、そこから焦点の 1 つまでの距離は準主軸の長さに相当します (
![]()
):
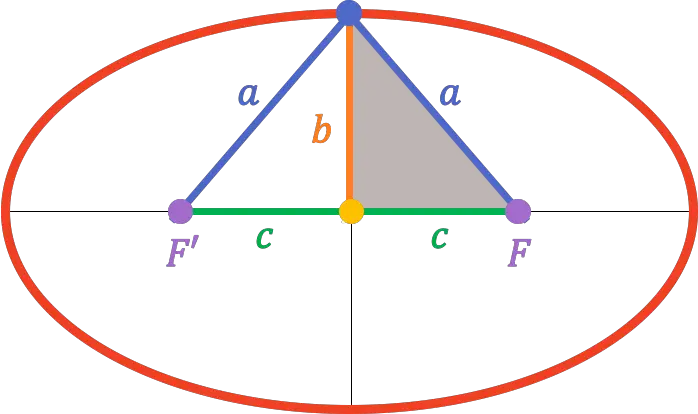
したがって、 ピタゴラスの定理から、主半軸、副半軸、および半焦点距離の間に存在する関係を見つけることができます。
![]()
この公式は、楕円を使用した演習の結果を計算するのに非常に便利なので、覚えておいてください。
楕円の離心率
明らかに、すべての楕円が同じではありませんが、より細長い楕円もあれば、より平坦な楕円もあります。したがって、特定の楕円がどの程度丸いかを測定するために使用される係数があります。この係数は偏心率と呼ばれ、次の式で計算されます。
![]()
金
![]()
は楕円の中心からその焦点の 1 つまでの距離です。
![]()
長半径の長さ。
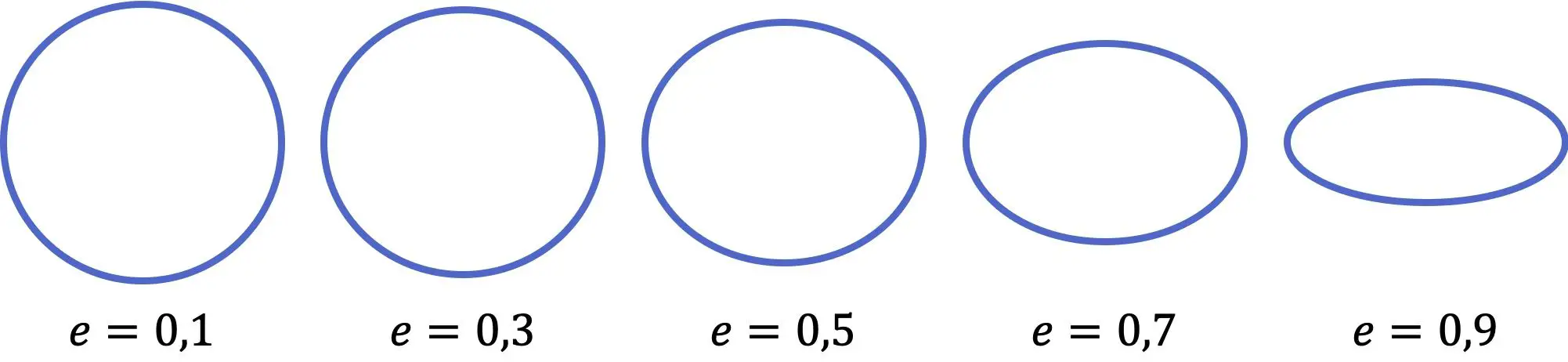
前の表現でわかるように、楕円の離心率の値が小さいほど円に近づき、一方、係数が大きいほど楕円は平坦になります。さらに、離心率の値の範囲は 0 (完全な円) から 1 (水平線) までで、両方を含みません。

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ bm{(y+1)^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\bm{144}} \bm{= 1}

![]()
d_v=6-(-4) =10 b =\cfrac{10}{2} = 5
![]()
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1C(3.1)
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( y-1)^2}}{\bm{25}} \bm{= 1}
![]()
a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}
![]()
\sqrt{24}
![]()
C(3,1) \bm{F\left(3+\sqrt{24},1}\right)} \bm{F\left(3-\sqrt{24},1}\right)}

![]()
d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a
![]()
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
最後に、この記事が役に立ったなら、 双曲線の公式と放物線の公式に関するページにもきっと興味を持っていただけるでしょう。双曲線と放物線とは何か、方程式、特性、例、演習問題などについて詳しく説明します。