ここでは有理関数とは何かを学びます。さらに、有理関数の定義域と漸近線の計算方法についても説明します。それだけでなく、有理関数のすべての特性が何であるかがわかります。最後に、有理関数に関する段階的な演習で練習することができます。
有理関数とは何ですか?
有理関数の定義は次のとおりです。
有理関数は 2 つの多項式の商によって形成される関数です。つまり、有理関数は分子と分母に多項式を持つ分数です。
有理関数は、分母が消える点での特異点によって特徴付けられます。
![]()
有理関数は分数関数とも呼ばれます。
一方、有理関数を無理関数と混同しないでください。非合理 (またはラジカル) 関数は、ルートで構成される関数です。
有理関数の例
有理関数の概念をよりよく理解するために、このタイプの関数の例をいくつか見ていきます。
- 分子と分母に 1 次多項式を使用する有理関数:
![]()
この種の有理関数は、ホモグラフ関数とも呼ばれます。
- 分子に定数、分母に多項式を持つ有理関数:
![]()
このような種類の有理関数は反比例関数と呼ばれ、反比例する量を数学的に定義するために使用されます。
- 分子に 3 次多項式、分母に 2 次多項式を持つ有理関数:
![]()
有理関数の領域
数を0で割ると無限大(∞)になるため、分母が0でない限り有理関数は常に存在します。
したがって、有理関数の定義域は、分母を打ち消す値を除くすべての実数で構成されます。
したがって、有理関数の定義域を取得するには、分母が 0 になるときを見つける必要があります。この点が定義域に属さない唯一の点となるためです。
例を解いて、有理関数の定義域がどのように計算されるかを見てみましょう。
![]()
まず分母を 0 に設定してから、結果の方程式を解きます。
![]()
![]()
したがって、x が -2 の場合、分母は 0 となり、関数は存在しません。したがって、関数の定義域は、x=-2 を除くすべての実数で構成されます。これは次のように述べられています。
![]()
有理関数の漸近線
有理関数の主な特性の 1 つは漸近線です。これはグラフ表現を決定するためです。
➤参照:関数のグラフィック表現
有理関数の漸近線は、関数のグラフが無限に近づくものの決して触れない線です。
漸近線には、垂直漸近線、水平漸近線、斜め漸近線の 3 種類があります。
以下に、有理関数が持つことができる 3 種類の漸近線を赤色でグラフ化しています。
有理関数の垂直漸近線

有理関数の水平漸近線

有理関数の斜め漸近線

ご覧のとおり、グラフから関数の漸近線を決定するのは非常に簡単ですが、グラフ表現を持たずに有理関数の漸近線を計算するのは非常に複雑です。このため、Web サイトで関数の漸近線がどのように計算されるかを確認することをお勧めします。
有理関数の特徴
有理関数には次の特徴があります。
![]()
- 上で見たように、有理関数の領域には、分数の分母を打ち消す値を除くすべての実数が含まれます。
- 一般に、有理関数の範囲 (または範囲) には、関数が水平漸近線を持つ値を除くすべての実数が含まれます。
- 有理関数はその領域全体で連続的です。言い換えれば、有理関数はその領域に属さない点で不連続性を示します。
- ほとんどの有理関数のグラフィック表現は 2 つの双曲線で構成されます。
- 有理関数の漸近線に関するいくつかの規則は、多項式の分子から推定できます。

そして分母多項式
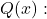
- 有理関数には、根となる点で垂直方向の漸近線があります。

しかし、これらはルーツではありません
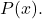
- の程度であれば、

の次数未満です

、線 y=0 は有理関数の水平漸近線です。
- の程度であれば、

~の程度よりも大きい

、有理関数には水平方向の漸近線がありません。
- の程度であれば、

の次数より大きい単位です

2 つの多項式には共通の根がなく、有理関数には斜めの漸近線があります。
- 有理関数には、根となる点で垂直方向の漸近線があります。
有理関数に関する演習を解決しました
演習 1
次の有理関数の定義域を求めます。
![]()
これは有理関数であるため、関数は ∞ を与えるため、分母を打ち消す数値を除くすべての数値で領域が構成されます。
そこで、どの数値がドメインに属していないのかを確認するために、整数の分母をゼロに設定します。
![]()
そして、結果として得られる方程式を解きます。
![]()
![]()
したがって、関数のドメインは、-2 を除く数値のみで構成されます。
![]()
演習 2
デカルト軸を使用して、次の有理関数のカットオフ点を見つけます。
![]()
X軸を伴う切断点
関数と X 軸の交点を見つけるには、次を解く必要があります。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
二次方程式の 2 つの解が得られたため、有理関数は次の 2 つの異なる点で横軸と交差します。
![]()
Y軸を伴う切断点
Y 軸との交点を見つけるには、計算する必要があります。
![]()
![]()
ゼロで割った数値は無限大を与える不確定性です。したがって、有理関数は Y 軸より上の点を通過しません。つまり、y 軸との交点がありません。
演習 3
次の有理関数をグラフにプロットします。
![]()
最初に行うことは、関数の定義域を計算することです。
![]()
![]()
![]()
![]()
関数のドメインがわかったら、値のテーブルを作成します。

最後に、得られた点をグラフ上に表して双曲線を描くだけで、有理関数を描くことができます。

演習 4
以下のグラフの有理関数の漸近線を決定します。
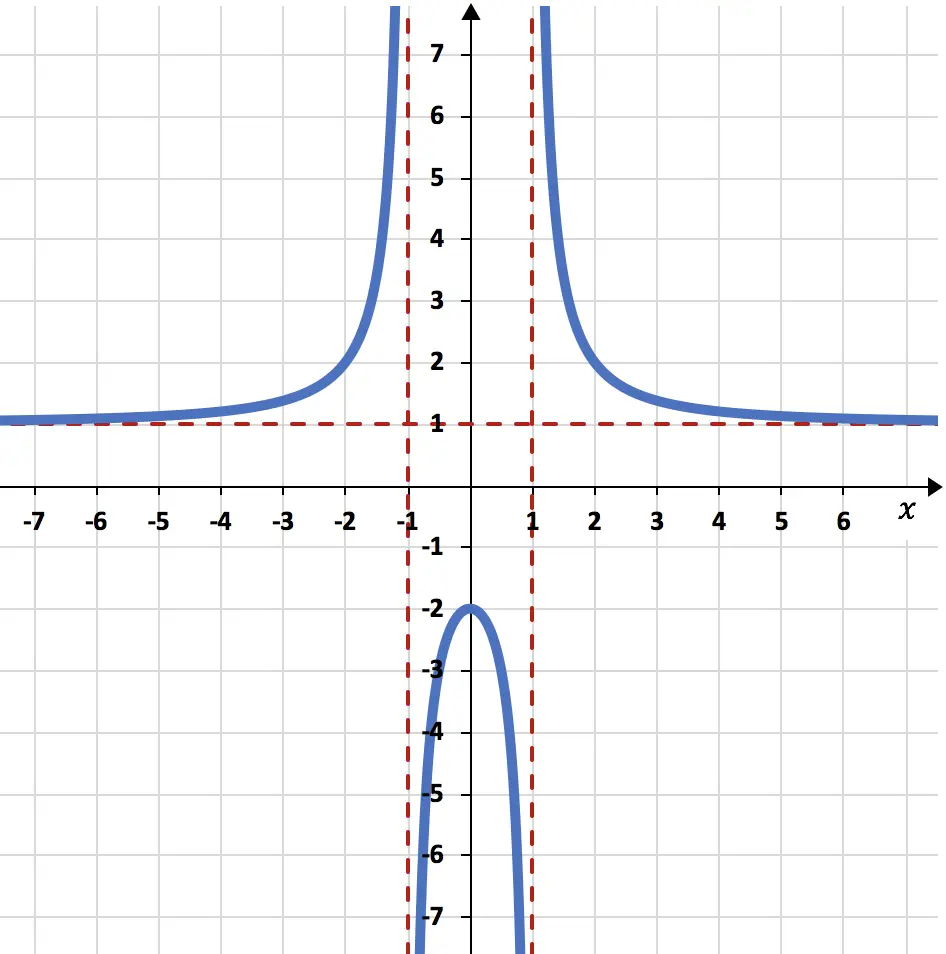
漸近線は赤い点線で表されているため、グラフ上で非常にはっきりと見えます。
この問題では、関数は水平線 y=1 に非常に近づいていますが、水平線に触れることはありません。したがって、有理関数には 1 つの水平漸近線 (y=1) があります。
同様に、関数のグラフ表示は垂直線 x=-1 および x=1 に非常に近くなりますが、これらの値には決して達しません。したがって、有理関数には、x=-1 と x=1 という 2 つの異なる垂直方向の漸近線があります。
演習 5
次の有理関数のすべての漸近線を計算します。
![]()
注:この演習を解決するには、まず関数の漸近線の計算方法に関する上記のリンクにアクセスし、説明を参照することをお勧めします。
垂直漸近線
関数の垂直漸近線を計算するには、まず関数の定義域を見つける必要があります。したがって、ドメインに属さない点を見つけるために、有理関数の分母を 0 に設定します。
![]()
![]()
![]()
したがって、関数の定義域は、-1 を除くすべての数値で構成されます。
![]()
したがって、x=-1 は垂直方向の漸近線になる可能性があります。これを確認するには、次の点での関数の極限を計算する必要があります。
![]()
したがって、この点での関数の極限は無限大を与えるため、x=-1 は有理関数の垂直漸近線になります。
水平漸近線
水平漸近線を決定するには、関数の無限限界を計算する必要があります。
![]()
![]()
この場合、分子と分母が同じ次数であるため、無限の間の不定無限極限の結果は、最高次数の x の係数の除算になります。
関数の 2 つの無限限界により 3 が得られるため、y=3 は有理関数の水平漸近線となります。
斜めの漸近線
水平方向の漸近線があるため、有理関数には斜め方向の漸近線はありません。